
4.已知满足约束条件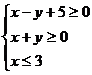 ,则
,则 的最小值是 ( )
的最小值是 ( )
A.5 B.-6 C.10 D.-10
3.在等差数列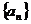 中,若
中,若 ,则该数列的前2008项的和是
,则该数列的前2008项的和是
( )
A.18072 B.3012 C.9036 D.12048
2.给出下面的三个命题:①函数 的最小正周期是
的最小正周期是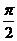 ②函数
②函数
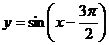 在区间
在区间 上单调递增③
上单调递增③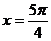 是函数
是函数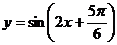 的图象的一条对称轴。其中正确的命题个数 ( )
的图象的一条对称轴。其中正确的命题个数 ( )
A.0 B.1 C.2 D.3
1.若 ,则
,则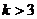 是方程
是方程 表示双曲线的 条件 ( )
表示双曲线的 条件 ( )
A.充分不必要 B.必要不充分 C.充要 D.既充分也不必要
22.(本小题满分14分)
已知 是函数
是函数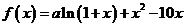 的一个极值点。
的一个极值点。
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求函数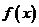 的单调区间;
的单调区间;
(Ⅲ)若直线 与函数
与函数 的图象有3个交点,求
的图象有3个交点,求 的取值范围.
的取值范围.
21.(本小题满分12分)
设p:实数x满足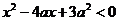 ,其中
,其中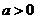 ,命题
,命题 实数
实数 满足
满足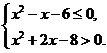 .
.
(Ⅰ)若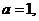 且
且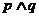 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(Ⅱ)若 是
是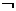
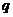 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
20.(本小题满分12分)
某公司计划2009年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为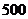 元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
19.(本小题满分12分)
已知函数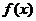 和
和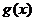 的图象关于原点对称,且
的图象关于原点对称,且 .
.
(Ⅰ)求函数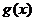 的解析式;
的解析式;
(Ⅱ)解不等式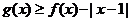 .
.
18.(本小题满分12分)
某市旅游部门开发一种旅游纪念品,每件产品的成本是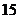 元,销售价是
元,销售价是 元,月平均销售
元,月平均销售 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
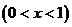 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为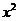 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是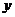 (元).
(元).
(Ⅰ)写出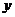 与
与 的函数关系式;
的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
17.(本小题满分12分)
已知二次函数 的图象过点(0,-3),且
的图象过点(0,-3),且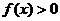 的解集
的解集 .
.
(Ⅰ)求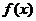 的解析式;
的解析式;
(Ⅱ)求函数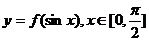 的最值.
的最值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com