2、竖直面内圆周运动

(1)　　　　　 绳(单轨，无支撑)：

绳只能给物体施加拉力，而不能有支持力。

这种情况下有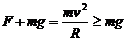

所以小球通过最高点的条件是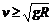，通过最高点的临界速度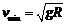

当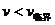(实际上小球还没滑到最高点就脱离了轨道)。

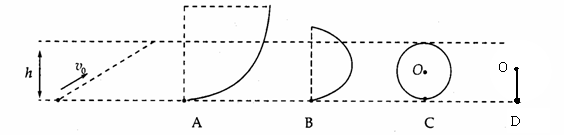
例1如图所示，小球以初速度为v₀从光滑斜面底部向上滑，恰能到达最大高度为h的斜面顶部。右图中A是内轨半径大于h的光滑轨道、B是内轨半径小于h的光滑轨道、C是内轨半径等于h光滑轨道、D是长为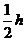的轻棒，其下端固定一个可随棒绕O点向上转动的小球。小球在底端时的初速度都为v₀，则小球在以上四种情况中能到达高度h的有(AB　 )

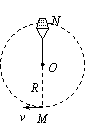例2 　如图所示的是杂技演员表演的“水流星”．一根细长绳的一端，系着一个盛了水的容器．以绳的另一端为圆心，使容器在竖直平面内做半径为R的圆周运动．N为圆周的最高点，M为圆周的最低点．若“水流星”通过最低点时的速度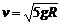．则下列判断正确的是(　)

A．“水流星”到最高点时的速度为零

B．“水流星”通过最高点时，有水从容器中流出

C．“水流星”通过最高点时，水对容器底没有压力

D．“水流星”通过最高点时，绳对容器有向下的拉力

解析：假设水能够通过最高点，则到达到最高点时的速度设为v₁，由机械能守恒定律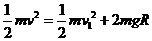得：，得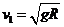，而当容器恰好能上升到最高点时的临界条件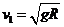，此时水对容器的压力为0时，C正确．

[答案]C　

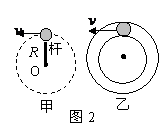(2)杆(双轨，有支撑)：对物体既可以有拉力，也可以有支持力，如图2所示。

①过最高点的临界条件：。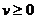

②在最高点，如果小球的重力恰好提供其做圆周运动的向心力，即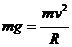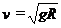，，杆或轨道内壁对小球没有力的作用。

当0<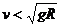时,小球受到重力和杆对球的支持力(或轨道内壁下侧对球的向上的支持力)，此二力的合力提供向心力；

当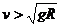时，小球受到重力和杆向下的拉力(或轨道内壁上侧对球竖直向下的压力)，这二力的合力提供向心力。

因此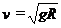，是小球在最高点受到杆的拉力还是支持力的分界速度，是受到轨道内壁下侧的弹力还是内壁上侧的弹力的分界速度。

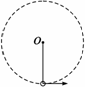例 　(04全国卷Ⅲ 20)如图所示,轻杆的一端有一个小球,另一端有光滑的固定轴O,现给球一初速度,使球和杆一起绕O轴在竖直面内转动,不计空气阻力,用F表示球到达最高点时杆对小球的作用力,则F (　　 )

A.一定是拉力　　　　　　　　　　　　　　　　　　　　　 B.一定是推力

C.一定等于零　　　　　　　　　　　　　　　　　　　　　 D.可能是拉力,可能是推力,也可能等于零

答案?D

解析　 最高点球受重力mg与杆的作用力F,由牛顿第二定律知mg+F=ma向=m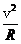(v为球在最高点的速度,R为球做圆周运动的半径)当v=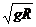时,F=0；当v>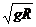时,F>0,即拉力；当v<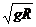时,F<0,即推力.故D对.　

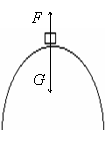解析 本题是物体在竖直面内圆周运动的典型模型――轻杆模型(有支撑的情况)，杆可以对物体有拉力，也可以有推力，对物体的弹力还可以为零，答案D。

[答案]D

(3)外轨(单轨，有支撑)，只能给物体支持力，而不能有拉力。

有支撑的小球，但弹力只可能向上，如车过桥．在这种情况下有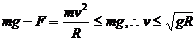： ，否则车将离开桥面，做平抛运动．

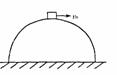例 如图所示，小物块位于半径为R的半球形物体顶端，若给小物块一水平速度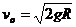，则物块　(　)

A．立即做平抛运动　 B．落地时水平位移为

C．落地速度大小为2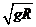　D．落地时速度方向与地面成45°角

解析：物体恰好不受轨道的支持力的情况下(物体在最高点做圆周运动)的临界条件是，最高点速度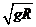为，因为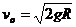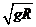＞，所以物体将从最高点开始做平抛运动，A正确；由平抛运动的规律可得：R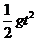＝，x=v₀t，所以可得x=2R，B答案正确；落地时竖直分速度，合速度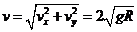，其方向与地面成45°角，CD正确．

[答案]ACD．

　 　由③⑥两式，消去t，可得到平抛运动的轨迹方程为。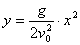

　 　　可见，平抛物体运动的轨迹是一条抛物线。

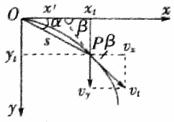　(2)一个有用的推论：平抛物体任意时刻瞬时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。

　证明：设物体被抛出后ts末时刻，物体的位置为P，其坐标为x_t(ts内的水平位移)和y_t(ts内的下落高度)；ts末的速度v_t的坐标分量为v_x、v_y，将v_t速度反向延长交x轴于x＇，如图：

则

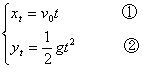
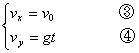　　由几何关系可知：，即

整理得：，∴。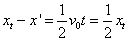

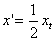可见，平抛运动物体某时刻的速度反向延长线交x轴坐标值为此时Ox方向位移的一半。

　(3)因平抛运动在竖直方向是匀变速直线运动，所以适合于研究匀变速运动的公式，如Δs=aT²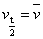，等同样也适用于研究平抛运动竖直方向的运动特点，这一点在研究平抛物体运动的实验中用得较多。

　(4)类平抛运动：凡具有合外力恒定且合外力垂直于初速度特征的曲线运动叫类平抛运动。

　此物体所做的运动可看成是某一方向的匀速直线运动和垂直此方向的匀加速直线运动，这类运动在电场中会涉及，处理方法与平抛运动类似。

圆周运动

1、匀速圆周运动

物体做匀速圆周运动必须具备两个条件：一是有初速度；二是其所受合力大小不变，方向始终与速度方向垂直而指向圆心。

　　　 由于物体所受合力大小不变，方向改变，指向圆心，称之向心力，则物体加速度大小不变。，

方向改变，指向圆心，称之向心加速度，其作用是只改变线速度方向，不能改变线速度大小。由于加速度不恒定，所以匀速圆周运动是非匀变速曲线运动。　　 星体运动是匀速圆周运动的特例。是星体间的万有引力“充当”圆运动的向心力。

　　　 (1)运动特点：轨迹是圆，速率不变。速度方向变化，即加速度方向指向圆心，加速度大小不变。根据牛顿第二定律，做匀速圆周运动的物体所受合力必指向圆心，永远与线速度方向垂直，其大小保持不变。匀速圆周运动属于变加速曲线运动。

　　　 (2)描述匀速圆周运动的物理量

　　　 转数n、频率f、周期T(转数也叫转速)如果时间以秒为单位则转速等于频率n=f，。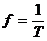

　　　 角速度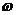　　　

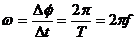
　　　 线速度v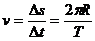　　　　

　　　 线速度与角速度之间的关系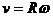：，这是一个重要公式。

　　　 向心加速度和向心力：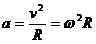

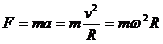
　　　 应该注意向心力不是性质力，而是效果力。重力、弹力、摩擦力、万有引力、电场力、磁场力……等等，任何一种性质力或几个性质力的合力、分力等等，只要它的效果是使质点产生向心加速度的，它就是向心力。

　　　 研究圆周运动，找出向心力是关键性的一步：

对匀速圆周运动来说，质点所受的所有力的合力充当向心力，对非匀速圆周运动来说，沿着半径方向的合力充当向心力，切线方向的合力改变速度大小。

(二)从动力学的角度分析 　对于平抛运动的物体只受重力作用，尽管其速度大小和方向时刻在改变，但其运动的加速度却恒为重力加速度g，因而平抛运动是一种匀变速曲线运动。

　平抛运动中，由于仅有重力对物体做功，因而若把此物体和地球看作一个系统，则在运动过程中，系统每时每刻都遵循机械能守恒定律。应用机械能守恒定律分析、处理此类问题，往往比单用运动学公式方便、简单得多。

知识要点：

平抛运动

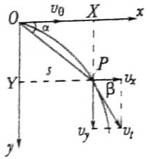　　　 (一)从运动学的角度分析 　平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动，以物体的出发点为原点，沿水平和竖直方向建立xOy坐标，如图所示：

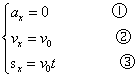则水平方向和竖直方向的分运动分别为 　　 水平方向 　　 竖直方向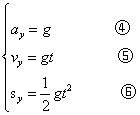

　　 平抛物体在时间t内的位移s可由③⑥两式推得 　　

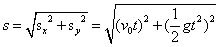
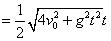
　　 位移的方向与水平方向的夹角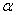由下式决定

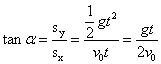
　　 平抛物体经时间t时的瞬时速度v_t可由②⑤两式推得 　　

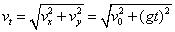
　　 速度v_t的方向与水平方向的夹角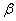可由下式决定

10.甲、乙二人参加普法知识竞答，共有10个不同的题目，其中选择题6个，判断题4个，甲、乙二人依次各抽一题.

(1)甲抽到选择题，乙抽到判断题的概率是多少？

(2)甲、乙二人中至少有一人抽到选择题的概率是多少？

分析：(1)是等可能性事件，求基本事件总数和A包含的基本事件数即可.(2)分类或间接法，先求出对立事件的概率.

解：(1)基本事件总数甲、乙依次抽一题有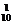CC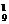种，事件A包含的基本事件数为CC，故甲抽到选择题，乙抽到判断题的概率为=.

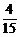(2)A包含的基本事件总数分三类：

甲抽到选择题,乙抽到判断题有CC；

甲抽到选择题,乙也抽到选择题有CC;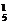

甲抽到判断题,乙抽到选择题有CC.

共CC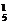+CC+CC.　 基本事件总数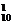CC，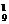

∴甲、乙二人中至少有一人抽到选择题的概率为:

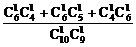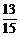=或P()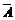

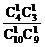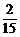==，P(A)=1－P()=.

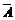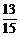[探索题]某人有5把钥匙，一把是房门钥匙，但忘记了开房门的是哪一把.于是，他逐把不重复地试开，问：

(1)恰好第三次打开房门锁的概率是多少？

(2)三次内打开的概率是多少？

(3)如果5把内有2把房门钥匙，那么三次内打开的概率是多少？

解：5把钥匙，逐把试开有A种等可能的结果.

(1)第三次打开房门,须把能开房门的钥匙放在第三位,结果有A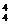种，因此第三次打开房门的概率P(A)=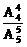=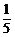.(另法)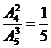

(2)三次内打开房门的结果有3A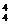种，因此，所求概率P(A)==.

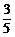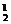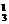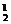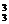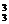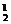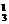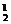(3)法1：三次内打开的结果包括：三次内恰有一次打开的结果有CAAA种；三次内恰有2次打开的结果有AA种.因此，三次内打开的结果有CA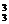AA+AA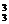种，所求概率

P(A)==.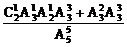

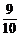法2:只计算三次,分只有一次打开,恰有两次打开:.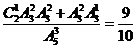

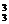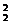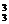法3：因5把内有2把房门钥匙，故三次内打不开的结果有AA种，从而三次内打开的结果有A－AA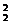种，所求概率P(A)==.

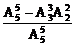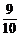9．从男生和女生共36人的班级中任意选出2人去完成某项任务，这里任何人当选的机会都是相同的，如果选出的2人有相同性别的概率是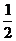，求这个班级中的男生，女生各有多少人?

解：　 设此班有男生n人(n∈N,n≤36)，则有女生(36-n)人，

从36人中选出有相同性别的2人，只有两种可能，即2人全为男生，或2人全为女生.

从36人中选出有相同性别的2人，共有(C_n²+C_36-n²)种选法.

因此，从36人中选出2人，这2人有相同性别的概率为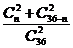

依题意，有＝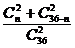

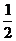
经过化简、整理，可以得到

n²-36n+315＝0.

所以n＝15或n＝21，它们都符合n∈N，n<36.

答：此班有男生15人，女生21人；或男生21人，女生15人.

8.把编号为1到6的六个小球，平均分到三个不同的盒子内，求：

(1)每盒各有一个奇数号球的概率；

(2)有一盒全是偶数号球的概率.

解：6个球平均分入三盒有C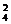CC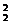种等可能的结果.

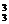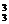(1)每盒各有一个奇数号球的结果有AA种，

所求概率P(A)==.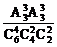

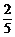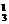(2)有一盒全是偶数号球的结果有(CC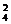)·CC，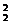

所求概率P(A)==.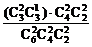

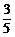7．某产品中有7个正品，3个次品，每次取一只测试，取后不放回，直到3只次品全被测出为止，求经过5次测试，3只次品恰好全被测出的概率。

解：“5次测试”相当于从10只产品中有序的取出5只产品，共有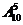种等可能的基本事件，“3只次品恰好全被测出”指5件中恰有3件次品，且第5件是次品，共有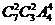种，所以所求的概率为。

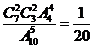5. 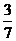;　 6. P==.

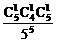[解答题]

4．分母4⁶，分子C₆¹C₅²A₄⁴,所求概率为；