
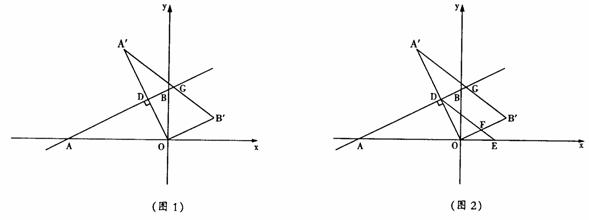
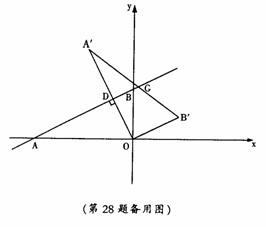
56.(2008黑龙江哈尔滨)如图,在平面直角坐标系中,直线y=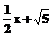 与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A´B´O,并使OA´⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.
与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A´B´O,并使OA´⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.
(1)求点D的坐标;
(2)连接DE,当DE与线段OB´相交,交点为F,且四边形DFB´G是平行四边形时,(如图2)求此时线段DE所在的直线的解析式;
(3)若以动点为E圆心,以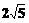 为半径作⊙E,连接A´E,t为何值时。Tan∠EA´B´=
为半径作⊙E,连接A´E,t为何值时。Tan∠EA´B´=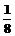 ?并判断此时直线A´O与⊙E的位置关系,请说明理由。
?并判断此时直线A´O与⊙E的位置关系,请说明理由。
压轴题2 答案
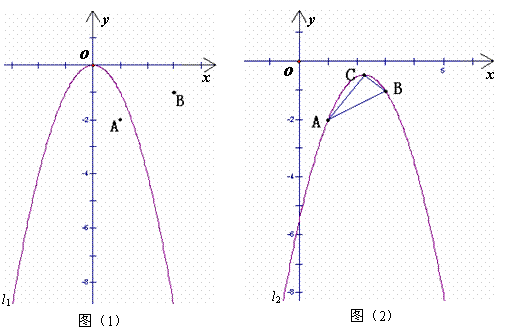
55. (2008湖南株洲)如图(1),在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,-1),二次函数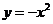 的图象为
的图象为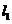 .
.
(1)平移抛物线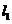 ,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可).
,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可).
(2)平移抛物线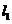 ,使平移后的抛物线过A、B两点,记抛物线为
,使平移后的抛物线过A、B两点,记抛物线为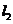 ,如图(2),求抛物线
,如图(2),求抛物线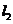 的函数解析式及顶点C的坐标.
的函数解析式及顶点C的坐标.
(3)设P为y轴上一点,且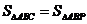 ,求点P的坐标.
,求点P的坐标.
(4)请在图(2)上用尺规作图的方式探究抛物线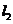 上是否存在点Q,使
上是否存在点Q,使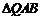 为等腰三角形. 若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.
为等腰三角形. 若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.
54.(2008贵州贵阳)某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加 元.求:
元.求:
(1)房间每天的入住量 (间)关于
(间)关于 (元)的函数关系式.(3分)
(元)的函数关系式.(3分)
(2)该宾馆每天的房间收费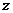 (元)关于
(元)关于 (元)的函数关系式.(3分)
(元)的函数关系式.(3分)
(3)该宾馆客房部每天的利润 (元)关于
(元)关于 (元)的函数关系式;当每个房间的定价为每天多少元时,
(元)的函数关系式;当每个房间的定价为每天多少元时,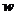 有最大值?最大值是多少?(6分)
有最大值?最大值是多少?(6分)
53.
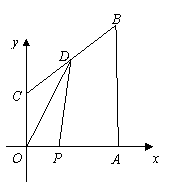
 (2008湖北黄冈)已知:如图,在直角梯形
(2008湖北黄冈)已知:如图,在直角梯形 中,
中,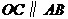 ,以
,以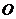 为原点建立平面直角坐标系,
为原点建立平面直角坐标系,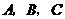 三点的坐标分别为
三点的坐标分别为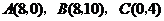 ,点
,点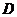 为线段
为线段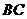 的中点,动点
的中点,动点 从点
从点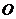 出发,以每秒1个单位的速度,沿折线
出发,以每秒1个单位的速度,沿折线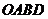 的路线移动,移动的时间为
的路线移动,移动的时间为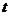 秒.
秒.
(1)求直线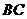 的解析式;
的解析式;
(2)若动点 在线段
在线段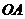 上移动,当
上移动,当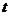 为何值时,四边形
为何值时,四边形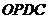 的面积是梯形
的面积是梯形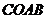 面积的
面积的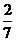 ?
?
(3)动点 从点
从点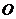 出发,沿折线
出发,沿折线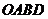 的路线移动过程中,设
的路线移动过程中,设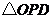 的面积为
的面积为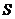 ,请直接写出
,请直接写出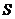 与
与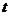 的函数关系式,并指出自变量
的函数关系式,并指出自变量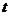 的取值范围;
的取值范围;
 (4)当动点
(4)当动点 在线段
在线段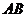 上移动时,能否在线段
上移动时,能否在线段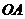 上找到一点
上找到一点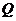 ,使四边形
,使四边形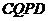 为矩形?请求出此时动点
为矩形?请求出此时动点 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
52.(2008浙江湖州)
已知:在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数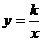 (k>0)的图象与AC边交于点E。
(k>0)的图象与AC边交于点E。
(1)求证:△AOE与△BOF的面积相等。
(2)记S=S△OEF-S△ECF,求当k为何值时,S有最大值,最大值为多少?
(3)请探索:是否存在这样的点F,做一日和尚撞一天钟得将CEF沿EF对折后,C点恰好落在OB上?若存在,求出点F的坐标,若不存在,请说明理由。
51.(2008江苏盐城)
如图甲,在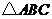 中,
中,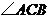 为锐角,点
为锐角,点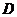 为射线
为射线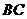 上一点,连接
上一点,连接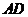 ,以
,以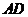 为一边且在
为一边且在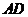 的右侧作正方形
的右侧作正方形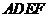 .
.
解答下列问题:
(1)如果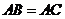 ,
,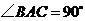 ,
,
①当点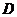 在线段
在线段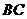 上时(与点
上时(与点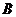 不重合),如图乙,线段
不重合),如图乙,线段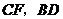 之间的位置关系为 ,数量关系为
.
之间的位置关系为 ,数量关系为
.
②当点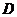 在线段
在线段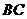 的延长线时,如图丙,①中的结论是否仍然成立,为什么?
的延长线时,如图丙,①中的结论是否仍然成立,为什么?

(2)如果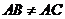 ,
,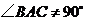 ,点
,点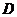 在线段
在线段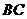 上运动.
上运动.
试探究:当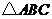 满足一个什么条件时,
满足一个什么条件时,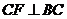 (点
(点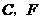 重合除外)?画出相应图形,并说明理由.(画图不写作法)
重合除外)?画出相应图形,并说明理由.(画图不写作法)
(3)若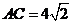 ,
,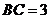 ,在(2)的条件下,设正方形
,在(2)的条件下,设正方形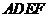 的边
的边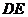 与线段
与线段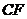 相交于点
相交于点 ,求线段
,求线段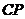 长的最大值.
长的最大值.
50.(2008湖北孝感)锐角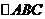 中,BC=6,
中,BC=6,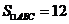 ,两动点M,N分别在边AB、AC上滑动,且
,两动点M,N分别在边AB、AC上滑动,且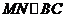 ,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与
,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与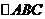 公共部分的面积为y(
公共部分的面积为y(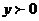 )
)
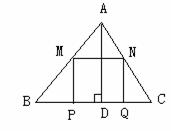
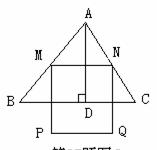
(1) 中边BC上高AD= ;
中边BC上高AD= ;
(2)当x= 时,PQ 恰好落在边BC上(如图1);
(3)当PQ在 外部时(如图2),求y关于x的函数关系式(注名x的取值范围),并求出x为何值时y最大,最大值是多少?
外部时(如图2),求y关于x的函数关系式(注名x的取值范围),并求出x为何值时y最大,最大值是多少?
49.(2008湖北襄樊)
如图15,四边形OABC是矩形,OA=4,OC=8,将矩形OABC沿直线AC折叠,使点B落在D处,AD交OC于E.
(1) 求OE的长;
(2) 求过O、D、C三点抛物线的解析式;
(3) 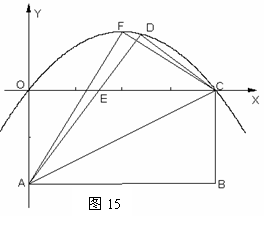 若F为过O、D、C三点抛物线的顶点,一动点P 从A点出发,沿射线AB以每秒一个单位长度的速度匀速运动,当运动时间t(秒)为何值时,直线PF把△FAC分成面积之比为1:3的两部分?
若F为过O、D、C三点抛物线的顶点,一动点P 从A点出发,沿射线AB以每秒一个单位长度的速度匀速运动,当运动时间t(秒)为何值时,直线PF把△FAC分成面积之比为1:3的两部分?
48.(2008湖北武汉)如图1,抛物线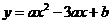 经过A(-1,0),C(3,2)两点,与
经过A(-1,0),C(3,2)两点,与 轴交于点D,与
轴交于点D,与 轴交于另一点B。
轴交于另一点B。
⑴求此抛物线的解析式;
⑵若直线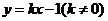 将四边形ABCD面积二等分,求
将四边形ABCD面积二等分,求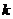 的值;
的值;
⑶如图2,过点E(1,-1)作EF⊥ 轴于点F,将△AEF绕平面内某点旋转180°后得△MNQ(点M,N,Q分别与点A,E,F对应),使点M,N在抛物线上,求点M,N的坐标.
轴于点F,将△AEF绕平面内某点旋转180°后得△MNQ(点M,N,Q分别与点A,E,F对应),使点M,N在抛物线上,求点M,N的坐标.




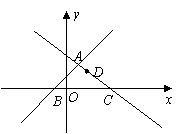
47.(2008山西太原)如图,在平面直角坐标系xOy中,直线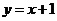 与
与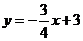 交于点A,分别交x轴于点B和点C,点D是直线AC上一个动点。
交于点A,分别交x轴于点B和点C,点D是直线AC上一个动点。
(1)求点A,B,C的坐标。
(2)当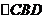 为等腰三角形时,求点D的坐标。
为等腰三角形时,求点D的坐标。
(3)在直线AB上是否存在点E,使得以点E,D,O,A为顶点的四边形是平行四边形?如果存在,直接写出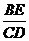 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com