1．掌握平面的基本性质，并会运用平面的基本性质证明点共线和线共面；

2．正方体ABCD-A₁B₁C₁D₁中，求以BD₁为棱，B₁BD₁与C₁BD₁为面的二面角的度数．

1．120°二面角α-l-β内有一点P，若P到两个面α，β的距离分别为3和1，求P到l的距

　 离．

2．将棱长为a的正四面体的一个面与棱长为a的正四棱锥的一个侧面吻合，则吻合后的几何

　 体呈现几个面？

　 分析：这道题，学生答“7个面”的占99.9%，少数应服从多数吗？

　 从例题中三个特征提供的思路在解决问题时各具特色，它们的目标分别是找“点”、“垂面”、

　 “垂线段”．事实上，我们只要找到其中一个，另两个就接踵而来．掌握这种关系对提高解

　 题技能和培养空间想象能力非常重要．

　 本题如果能融合三个特征对思维的监控，可有效地克服、抑制思维的消极作用，培养思维

　 的广阔性和批判性．

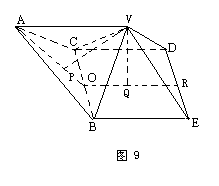
如图9，过两个几何体的高线VP，VQ的垂足

　 P，Q分别作BC的垂线，则垂足重合于O，且O为

　 BC的中点．OP延长过A，OQ延长交ED于R，考

　 虑到三垂线定理的环境背影，∠AOR为二面角

　 A-BC-R的平面角，结合特征(1)，(2)，可得VAOR

　 为平行四边形，VA∥BE，所以V，A，B，E共面．同

　 理V，A，C，D共面．所以这道题的正确答案应该

　 是5个面．

例3 　如图10，在正方体ABCD-A₁B₁C₁D₁中，E是BC的中点，F在AA₁上，且A₁F∶FA=1∶2，求平面B₁EF与底面A₁C₁所成的二面角大小的正切值．

分析：在给定的平面B₁EF与底面A₁C₁所成的二面角中，没有出现二面角的棱，我们可以设法在二面角的两个面内找出两个面的共点，则这两个公共点的连线即为二面角的棱，最后借助这条棱作出二面角的平面角．

略解：如图10．在面BB₁CC₁内，作EH⊥B₁C₁于H，连结HA₁，显然直线EF在底面A₁C₁的射影为HA₁．

延长EF，HA₁交于G，过G，B₁的直线为所求二面角的棱．

在平面A₁B₁C₁D₁内，作HK⊥GB₁于K，连EK，

则∠HKE为所求二面角的平面角．

在平面A₁B₁C₁D₁内，作B₁L⊥GH于L，利用Rt△GLB₁∽Rt△GKH，可求得KH．

又在Rt△EKH中，设EH=a，容易得到：所求二面角大小的正切值

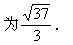
注：我们也可以不直接作出二面角的平面角，而通过等价变换或具体的计算得出其平面角的大小．我们可以使用平移法．由两平面平行的性质可知，若两平行平面同时与第三个平面相交，那么这两个平行平面与第三个平面所成的二面角相等或互补．因而例3中的二面角不易直接作出其平面角时，可利用此结论平移二面角的某一个面到合适的位置，以便等价地作出该二面角的平面角．

略解：过F作A′B′的平行线交BB′于G，过G作B′C′的平行线交B′E于H，连FH．

显见平面FGH∥平面A′B′C′D′．

则二面角B′-FH-G的平面角度数等于

所求二面角的度数．　 过G作GM⊥HF，

垂足为M，连B′M，由三垂线定理知

B′M⊥HF．所以∠B′MG为二面角

B′-FH-G的平面角，其大小等于所求

二面角平面角的大小．

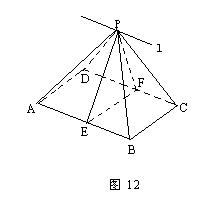例4 　已知：如图12，P是正方形ABCD所在

平面外一点，PA=PB=PC=PD=a，AB=a．

求：平面APB与平面CPD相交所成较大的二面角的余弦值．

分析：为了找到二面角及其平面角，必须依据题目的条件，找出

两个平面的交线．

解：因为　 AB∥CD，CD 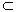平面CPD，AB 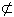平面CPD．

所以　 AB∥平面CPD．又　 P∈平面APB，且P∈平面CPD，

因此　 平面APB∩平面CPD=l，且P∈l．

所以　 二面角B-l-C就是平面APB和平面CPD相交所得到的一个二面角．

因为　 AB∥平面CPD，AB 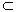平面APB，平面CPD∩平面APB=l，

所以　 AB∥l．过P作PE⊥AB，PE⊥CD．因为　 l∥AB∥CD，因此　 PE⊥l，PF⊥l，

所以　 ∠EPF是二面角B-l-C的平面角．

因为　 PE是正三角形APB的一条高线，且AB=a，

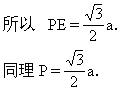
因为　 E，F分别是AB，CD的中点，所以　 EF=BC=a．

在△EFP中，

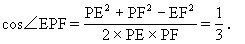
小结：二面角及其平面角的正确而合理的定位，要在正确理解其定义的基础上，掌握其基本特征，并灵活运用它们考察问题的背景．我们已经看到，定位是为了定量，求角的大小往往要化归到一个三角形中去解，因此寻找“垂线段”，把问题化归是十分重要的．

1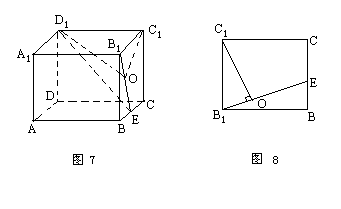．在正方体ABCD-A₁B₁C₁D₁中，棱长为2，E为BC的中点，求面B₁D₁E与面BB₁C₁C所成

　 的二面角的大小的正切值．

　 练习1的条件背景表明，面B₁D₁E

　 与面BB₁C₁C构成两个二面角，由特

　 征(2)可知，这两个二面角的大小

　 必定互补．

　 为创造一完整的三垂线定理的环境背

　 景，线段C₁D₁会让我们眼睛一亮，我

　 们只须由C₁(或D₁)作B₁E的垂线交

　 B₁E于O，然后连结OD₁(或OC₁)即得面

　 D₁B₁E与面CC₁B₁E所成二面角的平面角∠C₁OD₁，

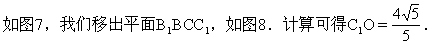
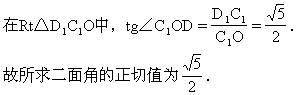
2．使学生掌握求二面角平面角的基本方法，不断提高分析问题和解决问题的能力．

1．使学生进一步掌握好二面角及二面角的平面角的概念；

18．(09年广东化学·24)(11分)

超细氧化铝是一种重要的功能陶瓷原料。

(1)实验室常以NH₄Al(SO₄)₂和NH₄HCO₃为原料，在一定条件下先反应生成沉淀NH₄AlO(OH)HCO₃,该沉淀高温分解即得超Al₂O₃,NH₄AlO(OH)HCO₃热分解的化学反应方程式　　　　　　　　 。

(2)NH₄Al(SO₄)₂·12H₂O的相对分子质量为453。欲配制100mlPH为2浓度约为0.1mol^-1的NH₄Al(SO₄)₂溶液,配制过程为

①用托盘天平称量NH₄Al(SO₄)₂·12H₂O固体　　　 g。

②将上述固体置于烧杯中　　　　　　　　　 。

(3)在0.1mol·l^-1NH₄Al(SO₄)₂溶液中，铝各形态的浓度(以Al³⁺计)的对数(lgc)随溶液ph变化的关系见下图

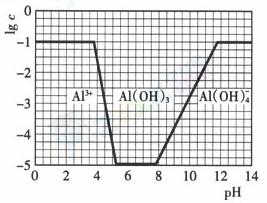
①用NaOH溶液调节(2)中溶液pH至7，该过程中发生反应的离子方程式有　　 ②请在答题卡的框图中，画出0.01mol·l^-1NH₄Al(SO₄)₂溶液中铝各形态的浓度的对数lgc随溶液pH变化的关系图，并进行必要的标注。

答案：(1)2NH₄AlO(OH)HCO₃2NH₃↑+Al₂O₃+3H₂O↑+2CO₂↑(2)将4.5g固体置于烧杯中，边加蒸馏水溶解边用玻璃棒搅拌，待完全溶解后，用玻璃棒移液至100ml的容量瓶中，用蒸馏水洗涤烧杯和玻璃棒2~3次，并将洗涤液转移到容量瓶中，加蒸馏水至刻度线2~3cm处应改用胶头滴管，上下振荡，静置，将配置好的溶液装入试剂瓶中，并贴上标签。

(3)图略。作图要点：起始与最终数值为-2；刚开始产生沉淀时PH要增大；完全沉淀和沉淀溶解时的PH应与原图一样；氢氧化铝完全溶解时的PH也是不变的二纵座标发生改变，所以线要与原图有所区别。

51．通过研究，小红提出了一系列降低铅对环境污染的建议，下列建议中不恰当的事()

A．使用无铅汽油

B．开发新的无铅燃料

C．倡导使用铅蓄电池作动力的电动车

D．燃煤电厂、金属冶炼厂的废气经除尘后排放。

答案：C