
8.几种特殊的分布列
(1)两点分布:对于一个随机试验,如果它的结果只有两种情况,则我们可用随机变量 ,来描述这个随机试验的结果。如果甲结果发生的概率为P,则乙结果发生的概率必定为1-P,均值为E
,来描述这个随机试验的结果。如果甲结果发生的概率为P,则乙结果发生的概率必定为1-P,均值为E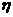 =p,方差为D
=p,方差为D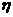 =p(1-p)。
=p(1-p)。
(2)超几何分布:重复进行独立试验,每次试验只有成功、失败两种可能,如果每次试验成功的概率为p,重复试验直到出现一次成功为止,则需要的试验次数是一个随机变量,用ξ表示,因此事件{ξ=n}表示“第n次试验成功且前n-1次试验均失败”。所以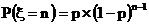 ,其分布列为:
,其分布列为:
|
ξ |
1 |
2 |
… |
n |
… |
|
P |
p |
p(1-p) |
… |
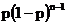 |
… |
(3)二项分布:如果我们设在每次试验中成功的概率都为P,则在n次重复试验中,试验成功的次数是一个随机变量,用ξ来表示,则ξ服从二项分布.则在n次试验中恰好成功k次的概率为: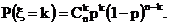
记ε是n次独立重复试验某事件发生的次数,则ε-B(n,p);
其概率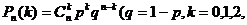 …
…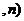 。期望Eε=np,方差Dε=npq。
。期望Eε=np,方差Dε=npq。
7.随机变量的均值和方差
(1)随机变量的均值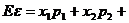 …;反映随机变量取值的平均水平。
…;反映随机变量取值的平均水平。
(2)离散型随机变量的方差: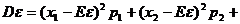 …
…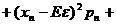 …;反映随机变量取值的稳定与波动,集中与离散的程度。
…;反映随机变量取值的稳定与波动,集中与离散的程度。
基本性质: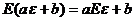 ;
;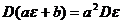 。
。
6.独立重复试验:若n次重复试验中,每次试验结果的概率都不依赖于其他各次试验的结果,则称这n次试验是独立的。
(1)两个相互独立事件同时发生的概率,等于每个事件发生的概率的积,即P(A·B)=P(A)·P(B);
(2)如果在一次试验中某事件发生的概率为P,那么在n次独立重复试验中这个事件恰好发生k次的概率:Pn(k)=C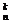 Pk(1-P)n-k。
Pk(1-P)n-k。
5.(理科)离散性随机变量的分布列
一般地,设离散型随机变量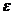 可能取得值为:
可能取得值为:
X1,X2,…,X3,…,
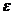 取每一个值Xi(I=1,2,…)的概率为P(
取每一个值Xi(I=1,2,…)的概率为P(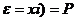 ,则称表
,则称表
 |
X1 |
X2 |
… |
xi |
… |
|
P |
P1 |
P2 |
… |
Pi |
… |
为随机变量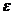 的概率分布,简称
的概率分布,简称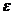 的分布列。
的分布列。
两条基本性质:①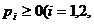 …);②P1+P2+…=1。
…);②P1+P2+…=1。
4.(理科)随机变量的概念,常用希腊字母ξ、η等表示。
对于随机变量可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。
注:随机变量ξ是关于试验结果的函数,即每一个试验结果对应着一个实数;随机变量ξ的线性组合η=aξ+b(a、b是常数)也是随机变量。
3.互斥事件有一个发生的概率公式为: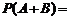
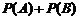 ;
;
相互独立事件同时发生的概率公式为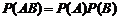 ;
;
如果事件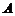 与
与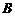 互斥,那么事件
互斥,那么事件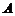 与
与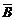 、
、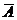 与
与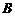 及事件
及事件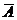 与
与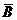 也都是互斥事件;
也都是互斥事件;
如果事件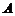 、
、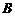 相互独立,那么事件
相互独立,那么事件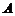 、
、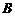 至少有一个不发生的概率是
至少有一个不发生的概率是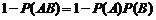 ;
;
条件概率:已知事件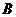 发生条件下事件
发生条件下事件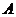 发生的概率称为事件
发生的概率称为事件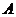 关于事件
关于事件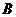 的条件概率,记作
的条件概率,记作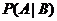 .
.
对任意事件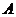 和
和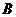 ,若
,若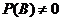 ,则“在事件
,则“在事件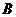 发生的条件下
发生的条件下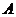 的条件概率”,记作P(A | B),定义为
的条件概率”,记作P(A | B),定义为
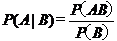
2. 随机事件的概率:事件A发生的频率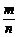 总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记作P(A)。
总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记作P(A)。
古典概型: ;
;
几何概型: ;
;
1.频率分布直方图、折线图与茎叶图
样本中所有数据(或数据组)的频率和样本容量的比,就是该数据的频率。所有数据(或数据组)的频率的分布变化规律叫做频率分布,可以用频率分布直方图、折线图、茎叶图来表示。
频率分布直方图:(1)求极差(即一组数据中最大值与最小值的差);(2)决定组距与组数;(3)将数据分组;(4)列频率分布表;(5)画频率分布直方图。注:频率分布直方图中小正方形的面积=组距× =频率。折线图:连接频率分布直方图中小长方形上端中点,就得到频率分布折线图。
=频率。折线图:连接频率分布直方图中小长方形上端中点,就得到频率分布折线图。
总体密度曲线:当样本容量足够大,分组越多,折线越接近于一条光滑的曲线,此光滑曲线为总体密度曲线。
9.几个重要的结论:
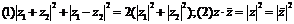 ;⑶
;⑶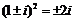 ;⑷
;⑷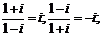
⑸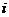 性质:T=4;
性质:T=4;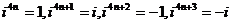 ;
;
(6)若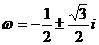 ,则
,则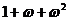 =0;(7)
=0;(7)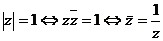 。
。
(8)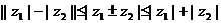 ;(9)
;(9)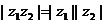 ;(9)
;(9)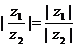 ;(9)
;(9)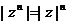 ;
;
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
8.复数的代数运算:设z1= a + bi , z2 = c + di (a,b,c,d∈R),则:
⑴复数的加减:z 1± z2 = ;类似于合并同类项;
⑵复数的乘法z1.z2 = ,即多项式乘法法则;
⑶复数的除法:z1÷z2 =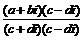 z2≠0),即转化为分母实数化;分子分母约分;或等式两边去分母。
z2≠0),即转化为分母实数化;分子分母约分;或等式两边去分母。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com