
7.(山东5)在R上定义运算⊙: 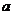 ⊙
⊙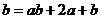 ,则满足
,则满足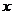 ⊙
⊙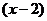 <0的实数
<0的实数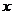 的取值范围为( ).
的取值范围为( ).
A.(0,2) B.(-2,1) C.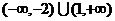 D.(-1,2)
D.(-1,2) 

[解析]:根据定义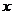 ⊙
⊙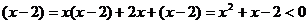 ,解得
,解得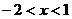 ,所以所求的实数
,所以所求的实数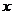 的取值范围为(-2,1),故选B.
的取值范围为(-2,1),故选B.
答案:B.
[命题立意]:本题为定义新运算型,正确理解新定义是解决问题的关键,译出条件再解一元二次不等式.
6.(福建9)在平面直角坐标系中,若不等式组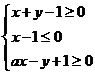 (
(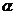 为常数)所表示的平面区域内的面积等于2,则
为常数)所表示的平面区域内的面积等于2,则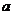 的值为
的值为
A. -5
B. 1
C. 2
D. 3


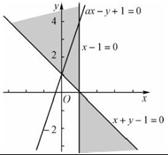 解析解析 如图可得黄色即为满足
解析解析 如图可得黄色即为满足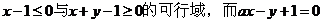 的直线恒过(0,1),故看作直线绕点(0,1)旋转,当a=-5时,则可行域不是一个封闭区域,当a=1时,面积是1;a=2时,面积是
的直线恒过(0,1),故看作直线绕点(0,1)旋转,当a=-5时,则可行域不是一个封闭区域,当a=1时,面积是1;a=2时,面积是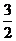 ;当a=3时,面积恰好为2,故选D.
;当a=3时,面积恰好为2,故选D.
5. (宁夏海南6)设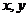 满足
满足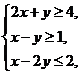 则
则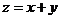
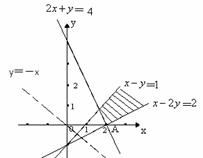 (A)有最小值2,最大值3 (B)有最小值2,无最大值
(A)有最小值2,最大值3 (B)有最小值2,无最大值
(C)有最大值3,无最小值 (D)既无最小值,也无最大值
[答案]B
[解析]画出不等式表示的平面区域,如右图,由z=x+y,得y=-x+z,令z=0,画出y=-x的图象,当它的平行线经过A(2,0)时,z取得最小值,最小值为:z=2,无最大值,故选.B
4.(天津9)设 的最大值为
的最大值为
A 2 B 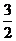 C 1 D
C 1 D 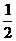
[答案]C
[解析]因为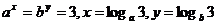 ,
,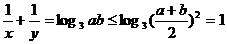
[考点定位]本试题考查指数式和对数式的互化,以及均值不等式求最值的运用,考查了变通能力。
3.(天津8)设函数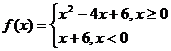 则不等式
则不等式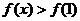 的解集是( )
的解集是( )
A 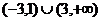 B
B 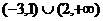
C 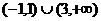 D
D 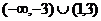
[答案]A
[解析]由已知,函数先增后减再增
当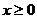 ,
,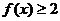
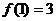 令
令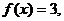
解得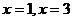 。
。 

当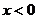 ,
,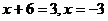
故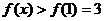 ,解得
,解得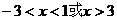
[考点定位]本试题考查分段函数的单调性问题的运用。以及一元二次不等式的求解。
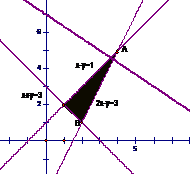
2.(天津2)设变量x,y满足约束条件: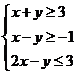 .则目标函数z=2x+3y的最小值为
.则目标函数z=2x+3y的最小值为
(A)6 (B)7 (C)8 (D)23
 [考点定位]本小考查简单的线性规划,基础题。
[考点定位]本小考查简单的线性规划,基础题。
解析:画出不等式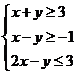 表示的可行域,如右图,
表示的可行域,如右图,
让目标函数表示直线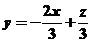 在可行域上平移,知在点B自目标函数取到最小值,解方程组
在可行域上平移,知在点B自目标函数取到最小值,解方程组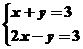 得
得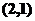 ,所以
,所以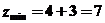 ,故选择B。
,故选择B。
1. (安徽3)不等式组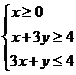 所表示的平面区域的面积等于
所表示的平面区域的面积等于
(A).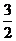 (B).
(B). 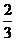 (C).
(C). 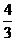 (D).
(D). 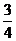

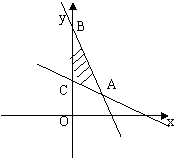 解析:不等式表示的平面区域如图所示阴影部分△ABC
解析:不等式表示的平面区域如图所示阴影部分△ABC
由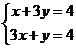 得A(1,1),又B(0,4),C(0,
得A(1,1),又B(0,4),C(0,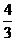 )
)
∴S△ABC=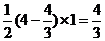 ,选C。
,选C。
2.应用函数与方程思想的常见题型
(1) 函数和方程相互渗透。对于函数y=f(x),当y=0时,就转化为方程f(x)=0,也可以把函数式y=f(x)看做二元方程y-f(x)=0。函数问题(例如求反函数,求函数的值域等)可以转化为方程问题来求解,方程问题也可以转化为函数问题来求解,如解方程f(x)=0,就是求函数y=f(x)的零点。
(2) 函数、不等式相互转化。有关的不等式、方程、最小值和最大值之类的问题,利用函数观点加以分析。对于函数y=f(x),当y>0时,就转化为不等式f(x)>0,借助于函数图像与性质解决有关问题,而研究函数的性质,也离不开解不等式。
(3) 数列的通项或前n项和是自变量为正整数的函数,用函数的观点处理数列问题十分重要。等差、等比数列中,通项公式、前n项和的公式,都可以看成n的函数,数列问题也可以用函数方法解决。
(4) 实际应用问题,翻译成数学语言,建立数学模型和函数关系式,应用函数性质或不等式等知识解答。
(5)遇到多元变量的数学问题中,选定合适的主变量,从而揭示其中的函数关系。
(6)函数f(x)=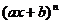 (n∈N*)与二项式定理是密切相关的,利用这个函数用赋值法和比较系数法可以解决很多二项式定理的问题。
(n∈N*)与二项式定理是密切相关的,利用这个函数用赋值法和比较系数法可以解决很多二项式定理的问题。
(7) 解析几何中的许多问题,例如直线和二次曲线的位置关系问题,需要通过解二元方程组才能解决,涉及到二次方程与二次函数的有关理论。
(8)立体几何中有关线段、角、面积、体积的计算,经常需要运用布列方程或建立函数表达式的方法加以解决。
已知f(x)=(x-a)(x-b)-2(a<b),并且α,β为f(x)=0的两根,α<β,则实数a,b,α,β的大小关系可能为( )
A、α<a<b<β B、a<α<β<b C、a<α<b<β D、α<a<β<b
答案:A 点评:未能抓住两个二次函数f(x)=(x-a)(x-b)-2与g(x)=(x-a)(x-b)的个性特征及联系,导致瞎猜。
1. 函数的思想,是用运动和变化的观点,分析和研究数学中的数量关系,建立函数关系或构造函数,运用函数的图像和性质去分析问题、转化问题,从而使问题获得解决。函数思想是对函数概念的本质认识,用于指导解题就是善于利用函数知识或函数观点观察、分析和解决问题。
方程的思想,就是分析数学问题中变量间的等量关系,建立方程或方程组,或者构造方程,通过解方程或方程组,或者运用方程的性质去分析、转化问题,使问题获得解决。方程的数学是对方程概念的本质认识,用于指导解题就是善于利用方程或方程组的观点观察处理问题。方程思想是动中求静,研究运动中的等量关系.
3.求轨迹方程的常用方法:
⑴直接法:直接通过建立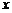 、
、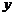 之间的关系,构成
之间的关系,构成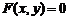 ,是求轨迹的最基本的方法.
,是求轨迹的最基本的方法.
⑵待定系数法:可先根据条件设所求曲线的方程,再由条件确定其待定系数,代回所列的方程即可.⑶代入法(相关点法或转移法).
⑷定义法:如果能够确定动点的轨迹满足某已知曲线的定义,则可由曲线的定义直接写出方程.
⑸交轨法(参数法):当动点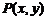 坐标之间的关系不易直接找到,也没有相关动点可用时,可考虑将
坐标之间的关系不易直接找到,也没有相关动点可用时,可考虑将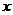 、
、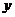 均用一中间变量(参数)表示,得参数方程,再消去参数得普通方程.
均用一中间变量(参数)表示,得参数方程,再消去参数得普通方程.
十四 定积分
(1)概念:用分点a=x0<x1<…<xi-1<xi<…xn=b把区间[a,b]等分成n个小区间,在每个小区间[xi-1,xi]上取任一点ξi(i=1,2,…n)作和式In=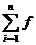 (ξi)△x(其中△x为小区间长度),把n→∞即△x→0时,和式In的极限叫做函数f(x)在区间[a,b]上的定积分,记作:
(ξi)△x(其中△x为小区间长度),把n→∞即△x→0时,和式In的极限叫做函数f(x)在区间[a,b]上的定积分,记作: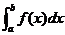 ,即
,即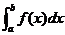 =
=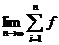 (ξi)△x。
(ξi)△x。
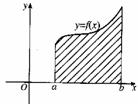 这里,a与b分别叫做积分下限与积分上限,区间[a,b]叫做积分区间,
这里,a与b分别叫做积分下限与积分上限,区间[a,b]叫做积分区间,
函数f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积式。
(2)基本的积分公式:
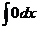 =C;
=C;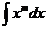 =
=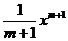 +C(m∈Q, m≠-1);
+C(m∈Q, m≠-1);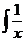 dx=ln
dx=ln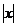 +C;
+C;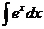 =
=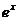 +C;
+C;
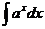 =
=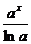 +C;
+C;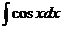 =sinx+C;
=sinx+C;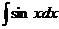 =-cosx+C(表中C均为常数)。
=-cosx+C(表中C均为常数)。
 (3)定积分的性质
(3)定积分的性质
①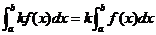 (k为常数);
(k为常数);
②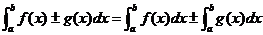 ;
;
③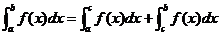 (其中a<c<b
(其中a<c<b 。
。
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com