
例1.已知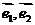 不平行,
不平行, ,
,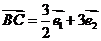 ,
,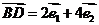 ,试判断:
,试判断: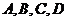 四点共面吗?并证明你的结论.
四点共面吗?并证明你的结论.
提示:⑴可以求得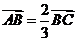 ,⑵
,⑵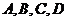 四点共线,从而共面.
四点共线,从而共面.
 例2.空间四边形
例2.空间四边形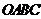 中,
中,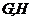 分别是
分别是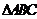 ,
,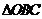 的重心,设
的重心,设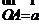 ,
,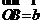 ,
,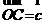 ,⑴试用向量
,⑴试用向量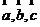 表示向量
表示向量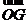 和
和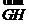 ;⑵证明:
;⑵证明: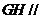 平面
平面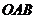 .
.
答案:⑴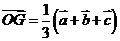 ,
,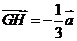 ;
;
例3.如图在正方体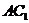 中,
中,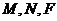 分别是棱
分别是棱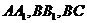 的中点,
的中点,
⑴求证: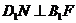 ;⑵求直线
;⑵求直线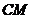 与
与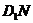 所成角的余弦值;
所成角的余弦值;
 ⑶求直线
⑶求直线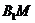 与
与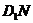 所成角的正弦值.
所成角的正弦值.
答案:⑵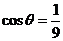 ;⑶
;⑶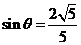 .
.
9.夹角和距离公式:
(1)夹角公式: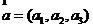 ,
,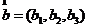 ,则
,则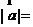 ;
;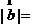 ;
;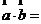 ;
;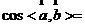 ;
;
(2)两点间距离公式: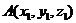 ,
,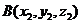 ,则
,则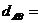 ;
;
(3)向量与平面垂直的意义:若表示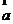 的有向线段
的有向线段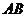 所在直线垂直于平面
所在直线垂直于平面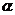 ,则称这个向量垂直于平面
,则称这个向量垂直于平面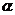 ,记为:
,记为: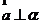 ,此时
,此时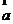 叫做平面
叫做平面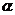 的法向量.
的法向量.
8.空间向量的坐标运算: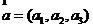 ,
,
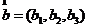 ,则
,则
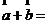 ;
;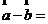 ;
;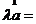 ;
;
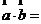 ;
;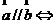 ;
;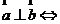 ;
;
若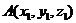 ,
,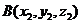 ,则
,则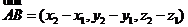 .
.
7.空间直角坐标系(右手直角坐标系):若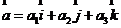 ,则
,则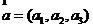
6.空间向量基本定理: ;
特别地,若基底为单位正交基底(常用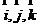 表示),则可以建立空间直角坐标系。
表示),则可以建立空间直角坐标系。
5.共面向量定理: ;
据此判断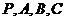 四点共面
四点共面 .
.
4.共线向量定理:
;空间直线的向量参数方程: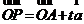 或
或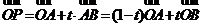 (其中
(其中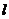 过点
过点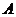 ,
,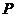 在直线
在直线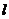 上,
上,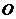 为空间任意一点,
为空间任意一点,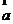 是
是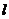 的方向向量
的方向向量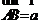 )由此判断
)由此判断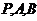 三点共线
三点共线 .
.
3.空间向量数量积:(1)主要性质:①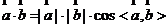 (可以用来求角);
(可以用来求角);
②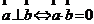 (可以用来证明线线垂直); ③
(可以用来证明线线垂直); ③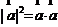 (可以用来求线段长).
(可以用来求线段长).
(2)运算律:①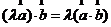 ; ②
; ②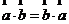 ; ③
; ③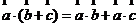 .
.
2.向量加法与数乘向量的基本性质:
(1)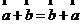 (2)
(2)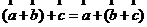 (3)
(3)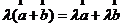 .
.
1.向量定义: ;相等向量: ;
共线(平行)向量: ;共面向量: ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com