
8. 如图,在三棱柱
如图,在三棱柱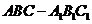 中,四边形
中,四边形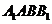 是菱形,四边形
是菱形,四边形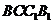 是矩形,
是矩形,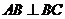 ,
,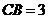 ,
,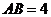 ,
,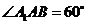 ,
,
(Ⅰ)求证:平面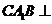 平面
平面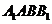 ;
;
(Ⅱ)求直线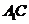 与平面
与平面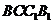 所成角的正切值;
所成角的正切值;
(Ⅲ)求点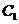 到平面
到平面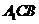 的距离。
的距离。
7.湖面上浮着一个球,湖水结冰后将球取出,冰上留下一个直径为24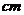 ,深为8
,深为8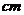 的空穴,则这个球的表面积为
,体积为
.
的空穴,则这个球的表面积为
,体积为
.
6.半径为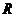 的球的任意两个大圆交于两点,这两点间的距离是
.
的球的任意两个大圆交于两点,这两点间的距离是
.
5.已知铜的单晶的外形是简单多面体,它有三角形和八边形两种晶面,如果铜的单晶有24个顶点,以每个顶点为一端都有三条棱,则单晶铜的三角形晶面有 个,八边形晶面有 个。
4.一个12面体共有8个顶点,其中2个顶点处各有6条棱,其它的顶点处都有相同数目的棱,则其它顶点处各有 条棱。
3.下列各图中,是正方体的表面展开图的共有 ( )
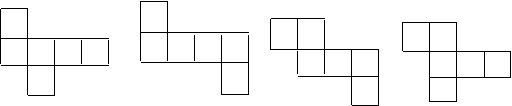
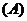 1个
1个
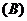 2个
2个
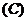 3个
3个
 4个
4个
2.已知半径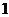 的球面上三点
的球面上三点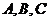 ,每两点之间的球面距离都是
,每两点之间的球面距离都是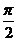 ,那么过
,那么过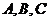 的截面与球心的距离是 .
的截面与球心的距离是 .
1.设地球半径为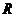 ,在北纬
,在北纬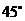 圈上有甲、乙两地,已知两地间的球面距离为
圈上有甲、乙两地,已知两地间的球面距离为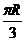 ,则此两地间的经度差为
.
,则此两地间的经度差为
.
例1.已知正四棱锥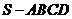 的底面边长为
的底面边长为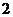 ,高
,高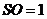 ,
,
(1)求证平面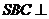 平面
平面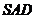 ;
;
(2)求相邻两侧面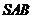 与
与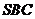 所成的角.
所成的角.
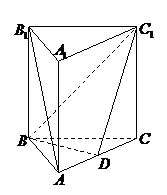
例2.如图,已知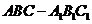 为正三棱柱,
为正三棱柱,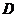 是
是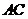 的中点,
的中点,
(Ⅰ)证明: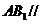 平面
平面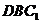 ;
;
(Ⅱ)若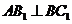 ,
,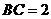 ,
,
①求二面角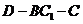 的大小;
的大小;
②若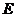 为
为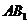 的中点,点
的中点,点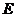 到平面
到平面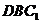 的距离.
的距离.
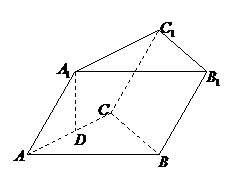 例3.已知斜三棱柱
例3.已知斜三棱柱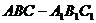 ,
,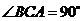 ,
,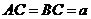 ,
,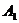 在底面
在底面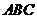 上的射影恰为
上的射影恰为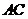 的中点
的中点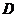 ,又
,又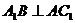 ,
,
(1)求证: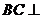 平面
平面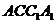 ;
;
(2)求点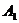 到
到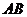 的距离;
的距离;
(3)求二面角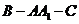 的正切值。
的正切值。
3.掌握欧拉定理并能用之进行简单的计算。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com