
9.函数的周期性:⑴若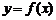 对
对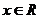 时
时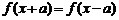 恒成立,则
恒成立,则 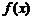 的周期为
的周期为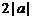 ;
;
⑵若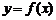 是偶函数,其图像又关于直线
是偶函数,其图像又关于直线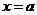 对称,则
对称,则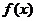 的周期为
的周期为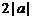 ;
;
⑶若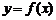 奇函数,其图像又关于直线
奇函数,其图像又关于直线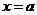 对称,则
对称,则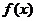 的周期为
的周期为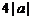 ;
;
⑷若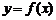 关于点
关于点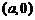 ,
,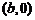 对称,则
对称,则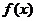 的周期为
的周期为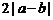 ;
;
⑸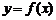 对
对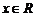 时,
时,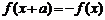 或
或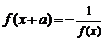 ,则
,则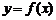 的周期为
的周期为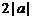 ;
;
8.函数图象的几种常见变换
⑴平移变换:左右平移----“左加右减”(注意是针对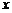 而言);上下平移----“上加下减”(注意是针对
而言);上下平移----“上加下减”(注意是针对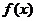 而言).
而言).
⑵翻折变换: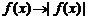 ;
;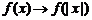 .
.
⑶对称变换:①证明函数图像的对称性,即证图像上任意点关于对称中心(轴)的对称点仍在图像上.
②函数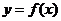 与
与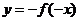 的图像关于原点成中心对称
的图像关于原点成中心对称
③函数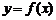 与
与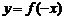 的图像关于直线
的图像关于直线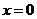 (
(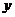 轴)对称;函数
轴)对称;函数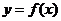 与函数
与函数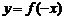 的图像关于直线
的图像关于直线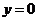 (
(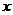 轴)对称;
轴)对称;
④函数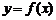 对
对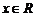 时,
时,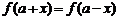 或
或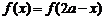 恒成立,则
恒成立,则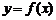 图像关于直线
图像关于直线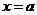 对称;
对称;
⑤若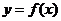 对
对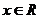 时,
时,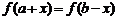 恒成立,则
恒成立,则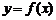 图像关于直线
图像关于直线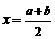 对称;
对称;
⑥函数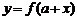 ,
,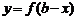 的图像关于直线
的图像关于直线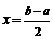 对称(由
对称(由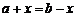 确定);
确定);
7.函数的奇偶性和单调性
⑴函数有奇偶性的必要条件是其定义域是关于原点对称的,确定奇偶性方法有定义法、图像法等;⑵若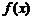 是偶函数,那么
是偶函数,那么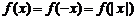 ;定义域含零的奇函数必过原点(
;定义域含零的奇函数必过原点(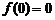 );
);
⑶判断函数奇偶性可用定义的等价形式: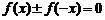 或
或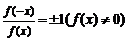 ;
;
注意:若判断较为复杂解析式函数的奇偶性,应先化简再判断;既奇又偶的函数有无数个
(如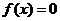 定义域关于原点对称即可).
定义域关于原点对称即可).
⑸奇函数在对称的单调区间内有相同的单调性;偶函数在对称的单调区间内有相反的单调性;
⑹确定函数单调性的方法有定义法、导数法,以及图像法和特值法(用于小题)等;
⑺复合函数单调性由“同增异减”判定. (提醒:求单调区间时注意定义域)
如:函数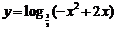 的单调递增区间是
的单调递增区间是 .(答:
.(答: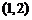 )
)
函数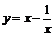 的单调增区间是
的单调增区间是 .(答:
.(答: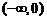 和
和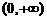 )你能画出图像吗?
)你能画出图像吗?
6.求函数解析式的常用方法:
⑴待定系数法(已知所求函数的类型); ⑵代换(配凑)法;
⑶方程的思想----对已知等式进行赋值,从而得到关于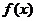 及另外一个函数的方程组;
及另外一个函数的方程组;
(4)坐标转移法。
5.求值域常用方法:
①配方法(二次函数类);②导数法(一般适用于高次多项式函数);③换元法(特别注意新元的范围).④三角有界法:转化为只含正弦、余弦的函数,运用三角函数有界性来求值域;⑤不等式法;⑥单调性法;⑦数形结合:根据函数的几何意义,利用数形结合的方法来求值域;⑧判别式法(慎用)
4.求定义域:
使函数解析式有意义(如:分母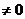 ;偶次根式被开方数非负;
;偶次根式被开方数非负;
对数真数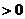 ,底数
,底数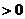 且
且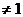 ;如
;如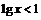 的解集:
的解集: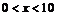 ;
;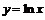 单调增区间
单调增区间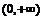 ;
;
零指数幂的底数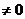 ;
;
实际问题有意义;若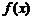 定义域为
定义域为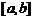 ,复合函数
,复合函数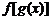 定义域由
定义域由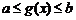 解出;若
解出;若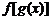 定义域为
定义域为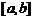 ,则
,则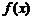 定义域相当于
定义域相当于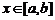 时
时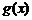 的值域.
的值域.
3.函数的三要素:定义域,值域,对应法则.研究函数的问题一定要注意定义域优先的原则.
2.函数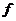 :
: 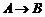 是特殊的映射.特殊在定义域
是特殊的映射.特殊在定义域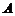 和值域
和值域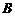 都是非空数集!据此可知函数图像与
都是非空数集!据此可知函数图像与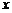 轴的垂线至多有一个公共点,但与
轴的垂线至多有一个公共点,但与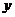 轴垂线的公共点可能没有,也可能有任意个.
轴垂线的公共点可能没有,也可能有任意个.
函数概念-函数图象-函数性态(定义域、值域、单调性、奇偶性、反函数、对称性、周期性)-特殊函数图象与性质-应用(内部应用、应用题)
1. 映射
①映射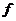 :
: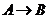 是:⑴ “一对一或多对一”的对应;
是:⑴ “一对一或多对一”的对应;
⑵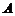 中元素必有象且
中元素必有象且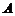 中不同元素在
中不同元素在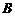 中可以有相同的象;
中可以有相同的象;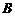 中元素不一定有原象(即象集
中元素不一定有原象(即象集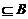 ).
).
②一一映射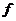 :
: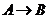 : ⑴“一对一”的对应;⑵
: ⑴“一对一”的对应;⑵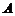 中不同元素的象必不同,
中不同元素的象必不同,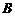 中元素都有原象.
中元素都有原象.
12.证明
⑴直接证明:综合法又叫顺推法或由因导果法。分析法又叫逆推证法或执果索因法。
用分析法证明不等式的逻辑关系是:
分析法的思维特点是:执果索因;
分析法的书写格式: 要证明命题B为真,只需要证明命题为真,
从而有……,这只需要证明命题为真,从而又有……
这只需要证明命题A为真,而已知A为真,故命题B必为真。
综合法:利用某些已经证明过的不等式(例如算术平均数与几何平均数定理)和不等式的性质推导出所要证明的不等式成立,这种证明方法通常叫做综合法,
用综合法证明不等式的逻辑关系是:
综合法的思维特点是:由因导果,即由已知条件出发,利用已知的数学定理、性质和公式,推出结论的一种证明方法。
⑵反证法的步骤:
1)假设命题的结论不成立,即假设结论的反面成立;
2)从这个假设出发,通过推理论证,得出矛盾;
3)由矛盾判定假设不正确,从而肯定命题的结论正确。
注意:可能出现矛盾四种情况:①与题设矛盾;②与反设矛盾;③与公理、定理矛盾④在证明过程中,推出自相矛盾的结论。
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com