
4..数量积的性质:设e是单位向量,〈a,e〉=θ.(1)e·a=a·e=|a|cosθ.
(2)当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|,特别地,a·a=|a|2,或|a|=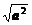 .
.
(3)a⊥b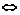 a·b=0.(4)cosθ=
a·b=0.(4)cosθ=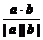 .(5)|a·b|≤|a||b|.
.(5)|a·b|≤|a||b|.
3. 设
设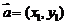 ,
,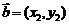 ,则
,则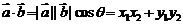 ;其几何意义是
;其几何意义是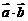 等于
等于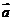 的长度与
的长度与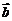 在
在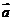 的方向上的投影的乘积;
的方向上的投影的乘积;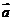 在
在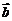 的方向上的投影
的方向上的投影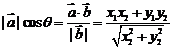 .
.
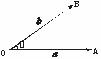
(1)向量的夹角:如下图,已知两个非零向量a和b,作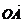 =a,
=a,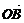 =b,
=b,
则∠AOB=θ(0°≤θ≤180°)叫做向量a与b的夹角,记作〈a,b〉.
注意: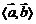 锐角
锐角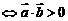 ,
,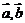 不同向;
不同向;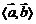 为直角
为直角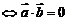 ;
;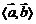 钝角
钝角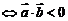 ,
,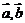 不反向.
不反向.
(2)数量积的定义:已知两个非零向量a和b,它们的夹角为θ,则数量|a||b|cosθ叫做a与b的数量积,记作a·b,即a·b=|a||b|cosθ.
(3)数量积的几何意义:数量积a·b等于a的模与b在a方向上的投影|b|cosθ的乘积.
提醒:一、向量夹角的范围:已知两个非零向量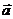 与
与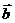 ,作
,作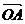 =
=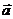 ,
, 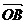 =
=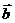 ,则∠AOB=
,则∠AOB=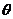 ,其中
,其中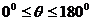 。
。
2.设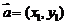 ,
,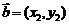 . (1)
. (1)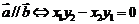 ;(2)
;(2)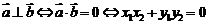 .
.
平面向量基本定理:如果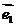 和
和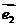 是同一平面内的两个不共线的向量,那么对该平面内的任一向量
是同一平面内的两个不共线的向量,那么对该平面内的任一向量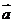 ,有且只有一对实数
,有且只有一对实数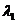 、
、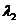 ,使
,使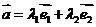 .
.
1.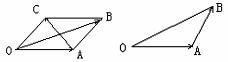 向量的运算
向量的运算
(1)向量加法设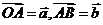 ,则
,则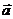 +
+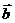 =
=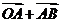 =
=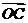 。
。
向量加法的“三角形法则”与“平行四边形法则”
(1)用平行四边形法则时,两个已知向量是要共始点的,和向量是始点与已知向量的始点重合的那条对角线,而差向量是另一条对角线,方向是从减向量指向被减向量。
(2) 三角形法则的特点是“首尾相接”,由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和;差向量是从减向量的终点指向被减向量的终点。
当两个向量的起点公共时,用平行四边形法则;当两向量是首尾连接时,用三角形法则。
向量加法的三角形法则可推广至多个向量相加:
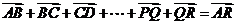 ,但这时必须“首尾相连”。
,但这时必须“首尾相连”。
(2)向量的减法
作图法: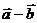 可以表示为从
可以表示为从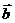 的终点指向
的终点指向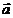 的终点的向量(
的终点的向量(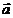 、
、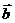 有共同起点)。
有共同起点)。
10.函数的特殊性质:(1)已知向量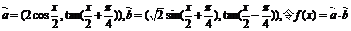 .求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调减区间为
.求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调减区间为
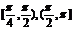 。(2)函数的值域可修补:如果
。(2)函数的值域可修补:如果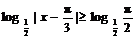 ,那
,那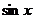 值域
值域 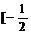 ,
,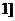 ;已知函数
;已知函数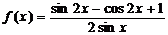 值域是
值域是 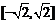 。
。
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
9.运用整体思想研究对称问题
研究三角复合函数的对称性的通法,一般是将其化归成研究基本三角函数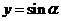 、
、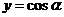 、
、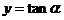 的对称性,
的对称性,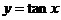 图像无对称轴,对称中心是
图像无对称轴,对称中心是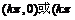
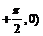 注意正切函数对称中心有两个。
注意正切函数对称中心有两个。
求三角函数的单调区间问题的通法是,直接观察基本三角函数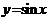 、
、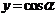 、
、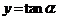 的单调区间,从而得到三角复合函数的单调区间。本题中函数的单调区间是是在特定的区间内的,一般是先求出所有的单调区间,然后在看哪些区间落在规定区域内。
的单调区间,从而得到三角复合函数的单调区间。本题中函数的单调区间是是在特定的区间内的,一般是先求出所有的单调区间,然后在看哪些区间落在规定区域内。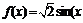
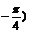 ,令
,令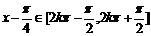
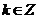 ) 则
) 则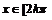
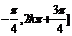 ,由于
,由于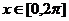 ,则
,则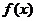 在
在 内单调递增区间为
内单调递增区间为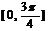 和
和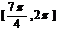 ;
;
求函数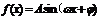 在某个给定的区域内的最值问题通用的方法是:根据自变量限定的区域,求出
在某个给定的区域内的最值问题通用的方法是:根据自变量限定的区域,求出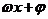 的整体的取值范围,从而把问题转化成求
的整体的取值范围,从而把问题转化成求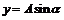 的值域问题。
的值域问题。
解复合的三角函数方程,一般是直接解相应的简单的三角函数,根据它们的解,利用整体思想,获得原方程的解。三角方程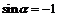 的解是
的解是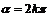
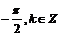 ,即
,即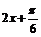 =
=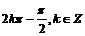 。{x|
。{x|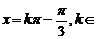 Z}.
Z}.
8. 函数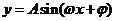 图象的画法:
图象的画法:
①“五点法”――设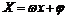 ,令
,令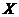 =0,
=0,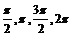 求出相应的
求出相应的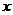 值,计算得出五点的坐标,描点后得出图象;
值,计算得出五点的坐标,描点后得出图象;
②图象变换法:将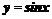 图象上的点沿
图象上的点沿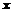 轴向
轴向 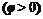 或向
或向 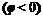 平移 个单位,得到函数
的图象,再将横坐标伸长(或缩短)到原来的 倍,到函数
的图象,最后将纵坐标伸长(或缩短)到原来的 倍,得到
平移 个单位,得到函数
的图象,再将横坐标伸长(或缩短)到原来的 倍,到函数
的图象,最后将纵坐标伸长(或缩短)到原来的 倍,得到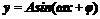 简图.
简图.
7.重要结论: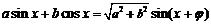 其中
其中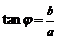 );重要公式
);重要公式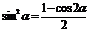 ;
;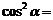
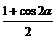 ;
;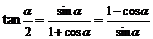 ;
;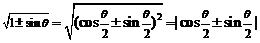 .
.
万能公式: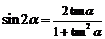 ;
;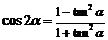 ;
;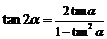 .
.
正弦型曲线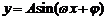 的对称轴
的对称轴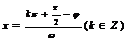 ;对称中心
;对称中心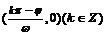 ;
;
余弦型曲线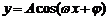 的对称轴
的对称轴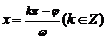 ;对称中心
;对称中心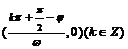 ;
;
6. 三角函数的化简、计算、证明的恒等变形的基本思路是:
①.三角函数恒等变形的基本策略。(1)常值代换:特别是用“1”的代换
(2)项的分拆与角的配凑。分拆项:sin2x+2cos2x= =1+cos2x;
配凑角:α=(α+β)-β,β=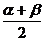 -
-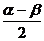 等。
等。
(3)降次与升次。即倍角公式降次与半角公式升次。
(4)化弦(切)法。(5)引入辅助角。asinθ+bcosθ=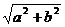 sin(θ+
sin(θ+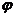 ),
),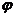 角的值由
确定。
角的值由
确定。
②证明三角等式的思路和方法。
(1)思路:利用三角公式进行化名,化角,改变运算结构,使等式两边化为同一形式。
(2)证明方法:综合法、分析法、比较法、代换法、相消法、数学归纳法。
③证明三角不等式的方法:比较法、配方法、反证法、分析法,利用函数的单调性,利用正、余弦函数的有界性,利用单位圆三角函数线及判别法等。
④解答三角高考题的策略:(1)发现差异:观察角、函数运算间的差异,即进行“差异分析”。
(2)寻找联系:运用相关公式,找出差异之间的内在联系。
(3)合理转化:选择恰当的公式,促使差异的转化。“一角二名三结构”。即首先观察角与角之间的关系;第二看函数名称之间关系,通常“切化弦”;第三观察代数式结构特点。角的变换:已知角与特殊角、已知角与目标角、已知角与其倍角或半角、两角与其和差角等变换.如: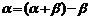 ;
;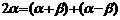 ;
;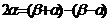
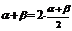 ;
;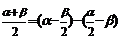 等;“
等;“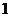 ”的变换:
”的变换: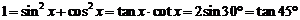 ;
; 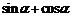
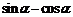 、
、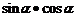 三者中任何一个,都可以视为一个整体,通过换元、平方等手段,互相转化。
三者中任何一个,都可以视为一个整体,通过换元、平方等手段,互相转化。
5.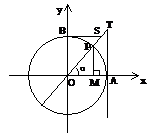 对于诱导公式,可用“奇变偶不变,符号看象限”概括;(注意:公式中始终视a为锐角)诱导公式(
对于诱导公式,可用“奇变偶不变,符号看象限”概括;(注意:公式中始终视a为锐角)诱导公式(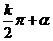 )可简记为:奇变偶不变,符号看象限. 其中奇是指
.偶是指 . 变是指
.看符号时要将
)可简记为:奇变偶不变,符号看象限. 其中奇是指
.偶是指 . 变是指
.看符号时要将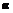 (不论具体是多少度)一律视为锐角.
(不论具体是多少度)一律视为锐角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com