
2.掌握球的概念和性质,能计算球的表面积、体积和球面距离;
1. 高考立体几何解答题多以棱柱、棱锥的形式出题,要掌握棱柱、直棱柱、正棱柱、平行六面体、长方体、正方体、正棱锥的性质,并能用于解题;
高考立体几何解答题多以棱柱、棱锥的形式出题,要掌握棱柱、直棱柱、正棱柱、平行六面体、长方体、正方体、正棱锥的性质,并能用于解题;
7.四面体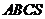 中,
中,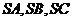 两两垂直,
两两垂直,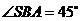 ,
,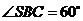 ,
,
 求:(1)
求:(1)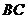 与面
与面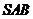 所成的角;(2)
所成的角;(2)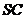 与面
与面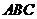 所成角的正弦值。
所成角的正弦值。
6. 正方体
正方体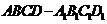 中,
中,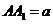 ,
,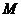 为
为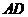 中点,
中点,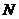 为
为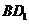 上一点,
上一点,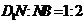 ,
,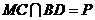 ,
,
(1)求证: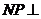 平面
平面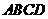 ;
;
(2)求平面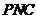 与平面
与平面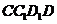 所成的角;
所成的角;
(3)求点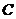 到平面
到平面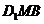 的距离。
的距离。
5.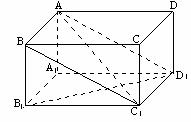 如图,在长方体
如图,在长方体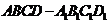 中,棱长
中,棱长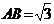 ,
,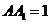 ,
,
截面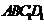 为正方形,
为正方形,
(Ⅰ)求直线 与平面
与平面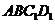 所成的角;
所成的角;
(Ⅱ)求二面角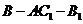 的正弦值。
的正弦值。
4.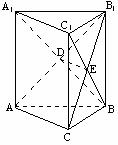 如图,直三棱柱
如图,直三棱柱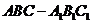 的侧棱和底面边长都是
的侧棱和底面边长都是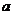 ,截面
,截面
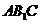 与截面
与截面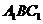 相交于
相交于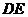 ,四面体
,四面体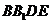 的体积为
的体积为
_________.
3.设平面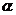 过
过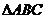 的重心,且
的重心,且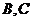 两点在
两点在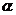 的同侧,
的同侧,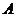 点在
点在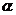 的另一侧,记
的另一侧,记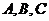 三
三
点到平面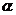 的距离分别为
的距离分别为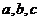 ,对任意满足上述条件的平面
,对任意满足上述条件的平面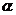 ,写出
,写出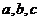 之间的关系
之间的关系
的一个等式 .
2.棱长为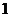 的正四面体在一平面
的正四面体在一平面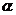 上的投影为
上的投影为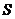 ,则
,则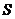 的最大值是 ( )
的最大值是 ( )
A.1 B.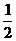 C.
C.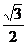 D.
D.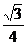
1.按照斜二测画,可能改变的是 ( )
A.两线段的平行性 B.平行于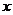 轴、
轴、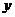 轴的线段的长度
轴的线段的长度
C.同方向上两线段的比 D.角的大小
例1.如图,直角梯形 中,
中,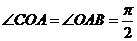 ,
,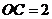 ,
,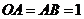 ,
,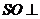 平面
平面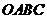 ,
,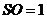 ,以
,以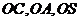 分别为
分别为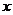 轴、
轴、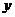 轴、
轴、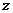 轴建立直角坐标系
轴建立直角坐标系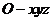 ,
,
(Ⅰ)求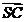 与
与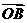 的夹角
的夹角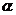 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(Ⅱ)设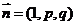 ,满足
,满足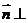 平面
平面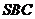 ,
,
求:①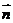 的坐标;②
的坐标;②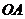 与平面
与平面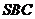 的夹角
的夹角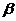 ;③
;③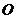 到平面
到平面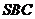 的距离;
的距离;
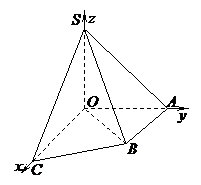 (Ⅲ)设
(Ⅲ)设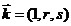 满足
满足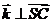 ,且
,且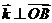 ,填写:①
,填写:①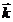 的坐标为 ;②异面直线
的坐标为 ;②异面直线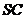 、
、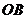 的距离为 .
的距离为 .
 例2.已知斜三棱柱
例2.已知斜三棱柱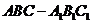 的侧面
的侧面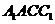 与底面
与底面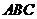 垂直,
垂直,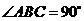 ,
,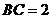 ,
,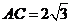 ,且
,且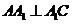 ,
,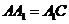 ,
,
(1)求侧棱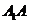 与底面
与底面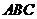 所成角的大小;
所成角的大小;
(2)求侧面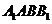 与底面
与底面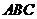 所成二面角的大小;
所成二面角的大小;
(3)求顶点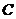 到侧面
到侧面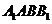 的距离.
的距离.
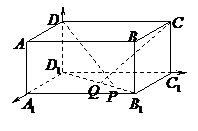
例3.在长方体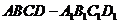 中,
中,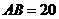 ,
,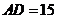 ,
,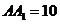 ,两动点
,两动点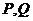 在线
在线
段 上,点
上,点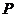 在
在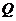 、
、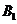 之间,异面直线
之间,异面直线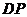 和
和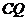 恰好互相垂直,如图所示,建立
恰好互相垂直,如图所示,建立
空间直角坐标系,(1)若测得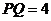 ,求点
,求点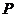 的坐标;(2)求
的坐标;(2)求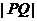 的最小值.
的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com