
3.直线到与它平行平面的距离、两个平行平面的距离,转化为点到平面的距离.
2.求点到平面的距离的方法有:(1)求点到平面的垂线段的长;(2)利用三棱锥的体积;利用平面的法向量:若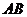 是平面
是平面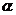 的斜线段(
的斜线段(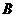 为斜足),
为斜足),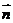 是平面
是平面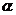 的任意一个法向量,则点
的任意一个法向量,则点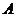 到平面
到平面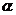 的距离
的距离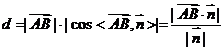 .
.
1.两条异面直线的距离是指两条异面直线的公垂线段的长度,求两条异面直线的距离的基本方法是找出或作出两条异面直线的公垂线段并计算其长度。两条异面直线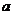 、
、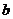 的距离也等于
的距离也等于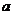 到过
到过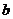 且平行
且平行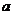 的平面的距离.
的平面的距离.
8.在四面体ABCD中,DA⊥面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.
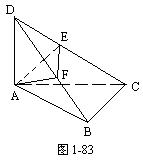
求证:(1)EF⊥DC;(2)平面DBC⊥平面AEF.

证明 如图1-83.(1)∵AD⊥面ABC.∴AD⊥BC.又∵∠ABC=90°.∴BC⊥AB.
∴BC⊥面DAB.∴DB是DC在面ABD内的射影.∵AF⊥DB.∴AF⊥CD(三垂线定理).
∵AE⊥CD.∴CD⊥平面AEF.∴CD⊥EF.
(2)∵CD⊥AE,CD⊥EF.∴CD⊥面AEF.∵CD 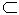 面BCD.∴面AEF⊥面BCD.
面BCD.∴面AEF⊥面BCD.
(3)由EF⊥CD,AE⊥CD ∴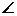 AEF为二面角B-DC-A的平面
AEF为二面角B-DC-A的平面
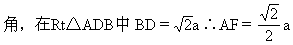
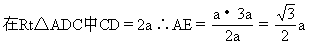
又∵AF⊥DB,AF⊥CD,BD∩CD=D ∴AF⊥平面DBC,
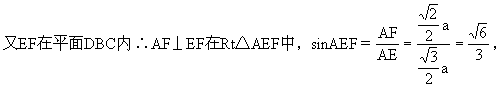
7.正四面体ABCD中,E是AD边的中点,求:CE与底面BCD所成角的正弦值.
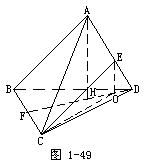 解 过A,E分别作AH⊥面BCD,EO⊥面BCD,H,O为垂足,
解 过A,E分别作AH⊥面BCD,EO⊥面BCD,H,O为垂足,
∴AH 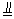 2OE,AH,OE确定平面AHD,连结OC,
2OE,AH,OE确定平面AHD,连结OC,
∠ECO即为所求.∵AB=AC=AD,∴HB=HC=HD
∵△BCD是正三角形,∴H是△BCD的中心,
连结DH并延长交BC于F,F为BC的中点,
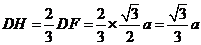 ,在Rt△ADH中,
,在Rt△ADH中,
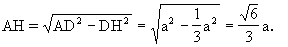
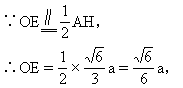
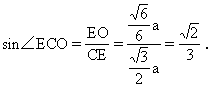
6.A是△BCD所在平面外的点,∠BAC=∠CAB=∠DAB=60°,AB=3,AC=AD=2.
(Ⅰ)求证:AB⊥CD; (Ⅱ)求AB与平面BCD所成角的余弦值.
5.正三棱锥的侧面与底面所成的二面角为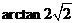 ,则它的侧棱与底面所成的角为
,则它的侧棱与底面所成的角为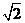
4.设正四棱锥S-ABCD的侧棱长为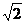 ,底面边长为
,底面边长为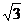 ,E是SA的中点,则异面直线BE与SC所成的角是 (C)
,E是SA的中点,则异面直线BE与SC所成的角是 (C)
A.30° B.45° C.60° D.90°
3.一条长为60的线段夹在互相垂直的两个平面之间,它和这两个平面所成的角分别为
45°和30°,这条线段的两个端点向平面的交线引垂线,则垂足间的距离是 (A)
A.30 B.20 C.15 D.12
2.下列命题中正确的是 (D)
A.过平面外一点作该平面的垂面有且只有一个
B.过直线外一点作该直线的平行平面有且只有一个
C.过直线外一点作该直线的垂线有且只有一条
D.过平面外的一条斜线作该平面的垂面有且只有一个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com