
4. 两角和与差的正弦、余弦、正切公式:①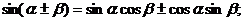
②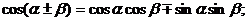 ③
③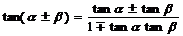 。④
。④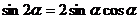 ;⑤
;⑤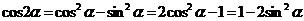 ;⑥
;⑥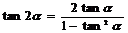 。
。
3. 角函数定义:角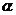 中边上任意一点
中边上任意一点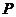 为
为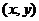 ,设
,设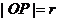 则:
则: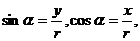
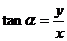
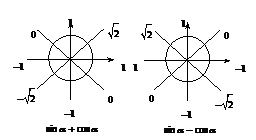 三角函数符号(“正号”)规律记忆口诀:“一全二正弦,三切四余弦”.
三角函数符号(“正号”)规律记忆口诀:“一全二正弦,三切四余弦”.
注意: 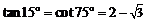 ;
;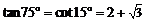 ;
;
三角函数线的特征是:
正弦线
“站在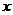 轴上(起点在
轴上(起点在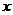 轴上)”、
轴上)”、
余弦线
“躺在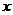 轴上(起点是原点)”、
轴上(起点是原点)”、
正切线
“站在点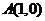 处(起点是
处(起点是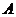 )”.
)”.
2.弧长公式: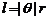 ;扇形面积公式:
;扇形面积公式: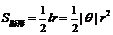 ;
;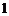 弧度(
弧度(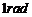 )≈
)≈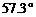 .
.
1.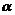 终边与
终边与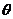 终边相同
终边相同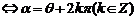 ;
;
10.数学归纳法公理:
如果(1)当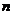 取第一个值
取第一个值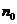 (例如
(例如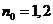 等)时结论正确;
等)时结论正确;
(2)假设当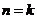 (
(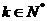 ,且
,且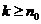 )时结论正确,证明当
)时结论正确,证明当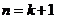 时结论也正确.
时结论也正确.
那么,命题对于从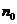 开始的所有正整数
开始的所有正整数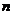 都成立.
都成立.
注意:(1)这两个步骤是缺一不可的.数学归纳法的步骤(1)是命题论证的基础,步骤(2)是判断命题的正确性能否递推下去的保证;
(2)在数学归纳法证明有关问题的关键,在第二步,即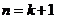 时为什么成立?
时为什么成立?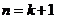 时成立是利用假设
时成立是利用假设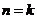 时成立,根据有关的定理、定义、公式、性质等数学结论推证
时成立,根据有关的定理、定义、公式、性质等数学结论推证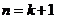 出时成立,而不是直接代入,否则
出时成立,而不是直接代入,否则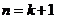 时也成假设了,命题并没有得到证明;
时也成假设了,命题并没有得到证明;
(3)用数学归纳法可证明有关的正整数问题,但并不是所有的正整数问题都是用数学归纳法证明,学习时要具体问题具体分析.
(4) 游戏:在一个平面上摆一排砖(每块砖都竖起),假定这排砖有无数块,我们要使所有的砖都倒下,只要做两件事就行了.第一,使第一块砖倒下;第二,保证前一块砖倒下后一定能击倒下一块砖.
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
9.利率问题:①单利问题:如零存整取储蓄(单利)本利和计算模型:若每期存入本金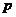 元,每期利率为
元,每期利率为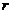 ,则
,则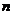 期后本利和为:
期后本利和为: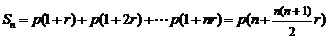 (等差数列问题);②复利问题:按揭贷款的分期等额还款(复利)模型:若贷款(向银行借款)
(等差数列问题);②复利问题:按揭贷款的分期等额还款(复利)模型:若贷款(向银行借款)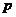 元,采用分期等额还款方式,从借款日算起,一期(如一年)后为第一次还款日,如此下去,分
元,采用分期等额还款方式,从借款日算起,一期(如一年)后为第一次还款日,如此下去,分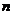 期还清.每期利率为
期还清.每期利率为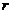 (按复利),那么每期等额还款
(按复利),那么每期等额还款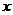 元应满足:
元应满足: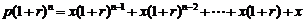 (等比数列问题).
(等比数列问题).
8. 求一般数列中的最大或最小项
“首正”的递减等差数列中,前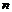 项和的最大值是所有非负项之和;“首负”的递增等差数列中,前
项和的最大值是所有非负项之和;“首负”的递增等差数列中,前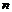 项和的最小值是所有非正项之和。法一:由不等式组
项和的最小值是所有非正项之和。法一:由不等式组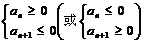 确定出前多少项为非负(或非正);法二:因等差数列前
确定出前多少项为非负(或非正);法二:因等差数列前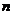 项是关于
项是关于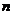 的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性
的二次函数,故可转化为求二次函数的最值,但要注意数列的特殊性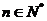
7.数列求和的方法:①公式法:等差数列,等比数列求和公式;②分组求和法;③倒序相加;④错位相减;⑤分裂通项法. 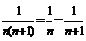 ;
;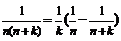 ;
;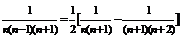 ;
;
 常见放缩公式:
常见放缩公式: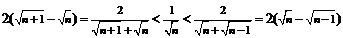 .
.
6.数列的通项的求法:⑴公式法:①等差数列通项公式;②等比数列通项公式.
⑵已知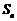 (即
(即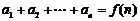 )求
)求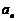 用作差法:
用作差法: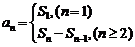 .
.
⑶已知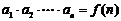 求
求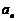 用作商法:
用作商法: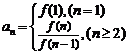 .
.
⑷若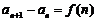 求
求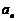 用迭加法. ⑸已知
用迭加法. ⑸已知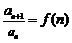 ,求
,求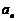 用迭乘法.
用迭乘法.
⑹已知数列递推式求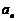 ,用构造法(构造等差、等比数列):①形如
,用构造法(构造等差、等比数列):①形如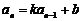 ,
,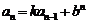 ,
,
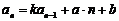 (
(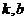 为常数)的递推数列都可以用待定系数法转化为公比为
为常数)的递推数列都可以用待定系数法转化为公比为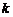 的等比数列后,再求
的等比数列后,再求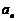 .②形如
.②形如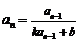 的递推数列都可以用 “取倒数法”求通项.
的递推数列都可以用 “取倒数法”求通项.
提醒:(1)求等比数列前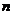 项和时,首先要判断公比
项和时,首先要判断公比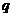 是否为1,再由
是否为1,再由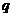 的情况选择求和公式的形式,当不能判断公比
的情况选择求和公式的形式,当不能判断公比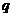 是否为1时,要对
是否为1时,要对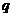 分
分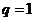 和
和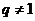 两种情形讨论求解。但是用整体思想可以不免讨论:
两种情形讨论求解。但是用整体思想可以不免讨论:
如:设等比数列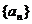 的公比为
的公比为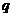 ,前
,前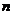 项和为
项和为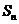 ,若
,若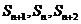 成等差数列,则
成等差数列,则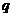 的值为
;
的值为
;
(2) 不要忽视对于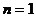 的验证:
的验证:
已知数列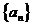 的前
的前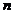 项和
项和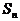 满足
满足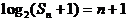 ,求数列
,求数列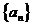 的通项公式。
的通项公式。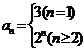
已知数列{an},满足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),则{an} n≥2的.通项 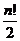
(3) 用构造法新构造出来的数列的首项容易搞错
已知数列{an}满足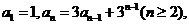 求an
。
求an
。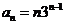
(4) 待定系数法求通项注意设元技巧
设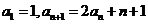 。求
。求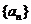 的通项公式;
的通项公式;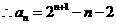
已知数列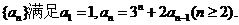 求an。
求an。
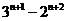
5.等比数列的性质
①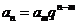 ,
,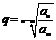 ;②若
;②若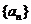 、
、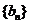 是等比数列,则
是等比数列,则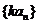 、
、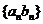 等也是等比数列;
等也是等比数列;
③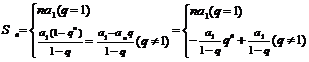 ;④
;④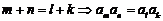 (反之不一定成立);
(反之不一定成立);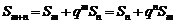 . ⑤等比数列中
. ⑤等比数列中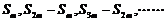 (注:各项均不为0)仍是等比数列. ⑥等比数列
(注:各项均不为0)仍是等比数列. ⑥等比数列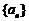 当项数为
当项数为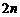 时,
时,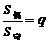 ;项数为
;项数为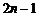 时,
时,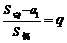 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com