
1.已知平面a的一条斜线a与平面a成q角,直线bÌa,且a,b异面,则a与b所成的角为
(A)
A.有最小值q,有最大值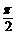 B.无最小值,有最大值
B.无最小值,有最大值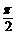 。
。
C.有最小值q,无最大值 D.有最小值q,有最大值p-q。
例1.正方体ABCD-A1B1C1D1中,M为C1D1中点.
(1)求证:AC1⊥平面A1BD.
(2)求BM与平面A1BD成的角的正切值.
解: (1)连AC,
∵C1C⊥平面ABCD, ∴C1C⊥BD.
又AC⊥BD, ∴AC1⊥BD.
同理AC1⊥A1B
∵A1B∩BD=B.∴AC1⊥平面A1BD.
(2)设正方体的棱长为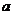 ,连AD1,AD1交A1D于E,连结ME,在△D1AC1中,ME∥AC1,
,连AD1,AD1交A1D于E,连结ME,在△D1AC1中,ME∥AC1,
∵AC1⊥平面A1BD.∴ME⊥平面A1BD.
 连结BE,则∠MBE为BM与平面A1BD成的角.在
连结BE,则∠MBE为BM与平面A1BD成的角.在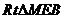 中,
中,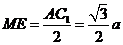 ,
,
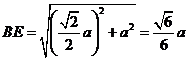 ,∴
,∴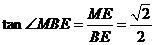 .
.
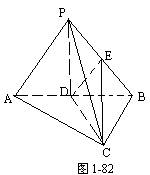
例2.如图,把等腰直角三角形ABC以斜边AB为轴旋转,
使C点移动的距离等于AC时停止,并记为点P.
(1)求证:面ABP⊥面ABC;
(2)求二面角C-BP-A的余弦值.
证明(1) 由题设知AP=CP=BP.
∴点P在面ABC的射影D应是△ABC的外心,
即D∈AB.∵PD⊥AB,PD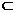 面ABP,
面ABP,
由面面垂直的判定定理知,面ABP⊥面ABC.
(2)解法1 取PB中点E,连结CE、DE、CD.
∵△BCP为正三角形,∴CE⊥BD.
△BOD为等腰直角三角形,∴DE⊥PB.∴∠CED为二面角C-BP-A的平面角.
又由(1)知,面ABP⊥面ABC,DC⊥AB,AB=面ABP∩面ABC,
由面面垂直性质定理,得DC⊥面ABP.∴DC⊥DE.因此△CDE为直角三角形.
设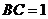 ,则
,则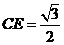 ,
,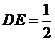 ,
,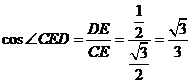 .
.
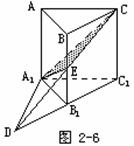
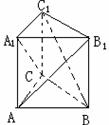
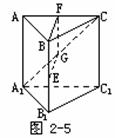 例3.如图所示,在正三棱柱
例3.如图所示,在正三棱柱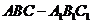 中,
中,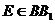 ,截面
,截面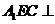 侧面
侧面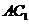 .
.
(1)求证: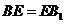 ;
;
(2)若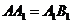 ,求平面
,求平面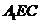 与平面
与平面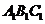
所成二面角(锐角)的度数.
证明:在截面A1EC内,过E作EG⊥A C,G是垂足,如图,
C,G是垂足,如图,
∵面A EC⊥面AC
EC⊥面AC ,∴EG⊥侧面AC
,∴EG⊥侧面AC .
.
取AC的中点F,分别连结BF和FC,由AB=BC得BF⊥AC.
∵面ABC⊥侧面AC ,∴BF⊥侧面AC
,∴BF⊥侧面AC ,
,
得BF∥EG.BF和EG确定一个平面,交侧面AC 于FG.
于FG.
∵BE∥侧面AC ,∴BE∥FG,四边形BEGF是
,∴BE∥FG,四边形BEGF是 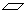 ,BE=FG.
,BE=FG.
 ∴BE∥AA
∴BE∥AA ,∴FG∥AA
,∴FG∥AA ,△AA
,△AA C∽△FGC.
C∽△FGC.
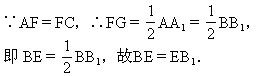
解:(2)分别延长CE和C1B1交于点D,连结A D.
D.
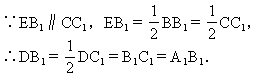
∵∠B A
A C
C =∠B
=∠B C
C A
A =60°,
=60°,
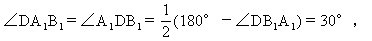
∴∠DA C
C =∠DA
=∠DA B
B +∠B
+∠B A
A C
C =90°,即 DA
=90°,即 DA ⊥A
⊥A C
C .
.
∵CC ⊥面A
⊥面A C
C B
B ,
,
由三垂线定理得DA ⊥A
⊥A C,所以∠CA
C,所以∠CA C
C 是所求二面角的平面角.且∠A
是所求二面角的平面角.且∠A C
C C=90°.
C=90°.
∵CC =AA
=AA =A
=A B
B =A
=A C
C ,∴∠CA
,∴∠CA C
C =45°,即所求二面角为45°.
=45°,即所求二面角为45°.
说明:如果改用面积射影定理,则还有另外的解法.
3.判定两个平面垂直,关键是在一个平面内找到一条垂直于另一个平面的直线。
两个平面垂直的性质定理是:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
2.二面角的大小用它的平面角来度量,求二面角大小的关键是找到或作出它的平面角(要证明)。作二面角的平面角经常要用三垂线定理,关键是过二面角的一个面内的一点向另一个面作垂线,并确定垂足的位置。若二面角的平面角难以作出,可考虑用射影面积公式求二面角的大小。
1.斜线与平面所成的角就是斜线与它在平面内的射影的夹角。求斜线与平面所成的角关键是找到斜线在平面内的射影,即确定过斜线上一点向平面所作垂线的垂足,这时经常要用面面垂直来确定垂足的位置。若垂足的位置难以确定,可考虑用其它方法求出斜线上一点到平面的距离。
9. 已知
已知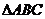 ,将
,将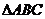 沿着平面
沿着平面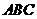 的法向量
的法向量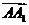 平移到
平移到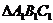 的位置,
的位置,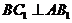 ,
,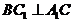 ,求证:
,求证: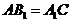 .
.
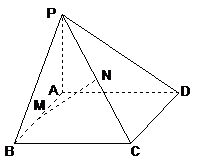
8.如图,点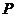 是矩形
是矩形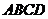 外一点,
外一点,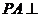 平面
平面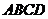 ,
,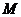 、
、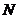 分别是
分别是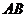 、
、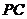 的中点,
的中点,
⑴求证: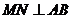 ;
;
 ⑵若
⑵若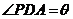 ,能否确定
,能否确定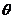 使得
使得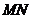 是异面直线
是异面直线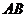 与
与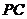 的公垂线?若可以确定
的公垂线?若可以确定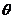 ,试求
,试求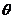 的值?若不能,说明理由.
的值?若不能,说明理由.
答案:⑵
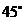 .
.

7.已知空间三个点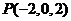 ,
,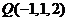 和
和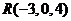 ,设
,设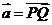 ,
,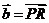 ,
,
⑴求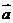 与
与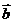 的夹角
的夹角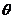 (用反三角函数表示);
(用反三角函数表示);
⑵试确定实数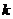 ,使
,使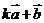 与
与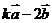 互相垂直;
互相垂直;
⑶试确定实数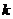 ,使
,使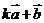 与
与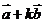 互相平行.
互相平行.
答案:⑴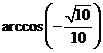 ;⑵
;⑵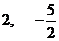 ;⑶
;⑶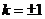 .
.
6.如图,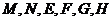 分别是四面体ABCD中各棱的中点,
分别是四面体ABCD中各棱的中点,
若此四面体的对棱相等,
则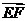 与
与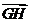 所成的角等于
所成的角等于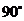 ;
;
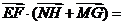 _0.
_0.
5.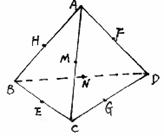 已知平面
已知平面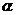 内的
内的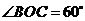 ,
,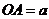 ,
,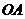 是平面
是平面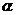 的斜线段,且
的斜线段,且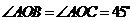 ,则点
,则点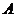 到平面
到平面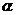 的距离为
的距离为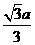 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com