
4. (理科)二项式定理:
⑴掌握二项展开式的通项: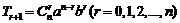 ;
;
⑵注意第r+1项二项式系数与第r+1项系数的区别.
3.(理科)排列数公式: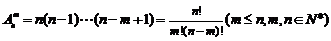 ,
, 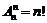 .
.
组合数公式: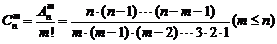 ,
,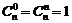 .
.
组合数性质: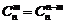 ;
;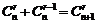 .
.
2. 总体特征数的估计:⑴样本平均数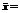 ;⑵方差
;⑵方差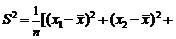
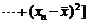 去估计总体方差。⑶样本标准差
去估计总体方差。⑶样本标准差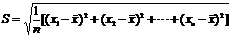 =
=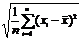
1.抽样方法;
⑴简单随机抽样:一般地,设一个总体的个数为N,通过逐个不放回的方法从中抽取一个容量为n的样本,且每个个体被抽到的机会 ,就称这种抽样为简单随机抽样。
注:①每个个体被抽到的概率为
;②常用的简单随机抽样方法有:抽签法;随机数法。③从含有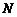 个个体的总体中,抽取
个个体的总体中,抽取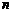 个体,则每个体第一次被抽到概率
个体,则每个体第一次被抽到概率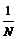 ,第二次被抽到概率
,第二次被抽到概率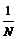 ,…,故每个个体被抽到的概率为
,…,故每个个体被抽到的概率为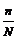 ,即每个个体入样的概率为
,即每个个体入样的概率为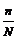 .
.
⑵系统抽样:步骤:①编号;②分段;③在第一段采用简单随机抽样方法确定其时个体编号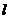 ;④按预先制定规则抽取样本。
;④按预先制定规则抽取样本。
⑶分层抽样:当总体差异比较明显,将总体分成几部分,然后按照各部分
进行抽样,这种抽样叫分层抽样。每个部分所抽取的样本个体数=该部分个体数
 ;
;
8.各类证明的依据:①线面平行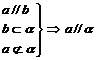 ;
;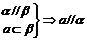 ;
;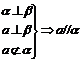 ;
;
②线线平行: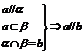 ;
;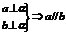 ;
;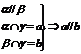 ;
;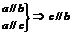
③面面平行: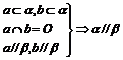 ;
;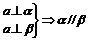 ;
;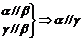
④线线垂直: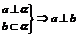 ;所成角900;
;所成角900;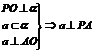 (三垂线);逆定理?
(三垂线);逆定理?
⑤线面垂直: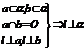 ;
;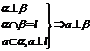 ;
;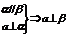 ;
;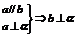
⑥面面垂直:二面角900; 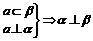 ;
;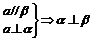
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
7.垂直
(1)直线和平面垂直
判定定理: 如果一条直线和一个平面内的两条 直线都垂直, 那么这条直线和这个平面垂直.
性质定理: 垂直于同一平面的 平行,垂直于同一条直线的 平行.
(2)平面和平面垂直
两个平面垂直的判定定理:如果一个平面经过另一个平面的 ,那么两个平面互相垂直.
两个平面垂直的性质定理:如果两个平面互相垂直, 那么在一个平面内 的直线垂直于另一个平面.
6. 平行
(1)直线和平面平行
判定定理:如果 一条直线和 一条直线平行,那么这条直线和这个平面平行.
性质定理: 如果一直线和一个平面平行,经过这直线平面和这个平面相交, 那么这条直线和 平行.
(2)平面和平面平行
判定定理: 如果一个平面内的两条 直线平行于另一平面,那么这两个平面平行.
推论: 如果一个平面内有两条 直线平行于另一平面内的两条直线, 那么这两个平面平行.
性质定理: 如果两个平行平面同时和第三个平面相交,那么它们的交线 .
5. 坐标系的建立:作空间直角坐标系O-xyz时,使∠xOy=135°(或45°),∠yOz=90°。
(1)让右手拇指指向x轴正方向,食指指向y轴正方向,中指能指向z轴的正方向,则称为右手直角坐标系;
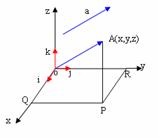 (2) OQ=x、OR=y、PA=z分别叫做点A的横坐标、纵坐标和竖坐标,记作A(x,y,z);
(2) OQ=x、OR=y、PA=z分别叫做点A的横坐标、纵坐标和竖坐标,记作A(x,y,z);
(3) 平面法向量:由直线与平面垂直的判断定理可知,不共线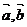 ,
,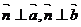 则
则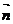 为平面
为平面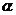 的法向量。
的法向量。
4.(理科)用向量方法求空间角和距离
⑴求异面直线所成的角:设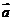 、
、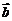 分别为异面直线
分别为异面直线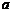 、
、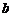 的方向向量,
的方向向量,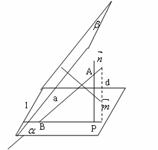 则两异面直线所成的角
则两异面直线所成的角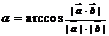 ;
;
⑵求线面角:设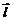 是斜线
是斜线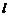 方向向量,
方向向量,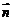 是平面
是平面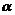 法向量, 与直线
法向量, 与直线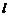 则斜线
则斜线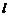 的锐夹角为
的锐夹角为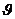 ,
,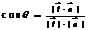 ,则斜线
,则斜线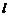 与平面
与平面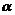 成角为
成角为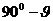 ,或
,或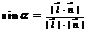 ;
;
注意: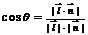 得到的角
得到的角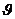 是法向量与直线的夹角,并不是直线和平面成的角;
是法向量与直线的夹角,并不是直线和平面成的角;
⑶求二面角(法一)在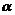 内
内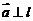 ,在
,在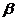 内
内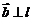 ,其方向如图(略),则
,其方向如图(略),则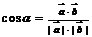 ;
;
(法二)设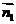 ,
,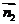 是两个半平面的法向量,其方向一个指向内侧,另一个指向外侧,则二面角
是两个半平面的法向量,其方向一个指向内侧,另一个指向外侧,则二面角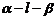 的平面角
的平面角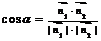 ;注:
;注: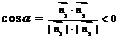 不能判断二面角是钝角,还要根据图形辨别;
不能判断二面角是钝角,还要根据图形辨别;
(4)求点面距离:设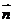 是
是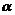 法向量,在
法向量,在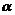 内取一点
内取一点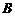 ,则
,则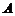 到
到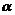 距离
距离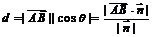 (即
(即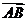 在
在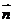 方向上投影的绝对值)
方向上投影的绝对值)
3.正四面体(设棱长为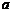 )的性质:
)的性质:
①全面积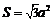 ;②体积
;②体积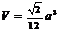 ;③对棱间的距离
;③对棱间的距离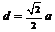 ;④相邻面所成二面角
;④相邻面所成二面角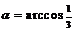 ;
;
⑤外接球半径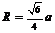 ;⑥内切球半径
;⑥内切球半径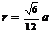 ;⑦正四面体内任一点到各面距离之和为定值
;⑦正四面体内任一点到各面距离之和为定值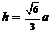 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com