
6、直线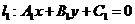 与直线
与直线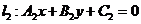 的位置关系:
的位置关系:
(1)平行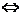
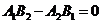 (斜率)且
(斜率)且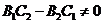 (在
(在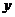 轴上截距);
轴上截距);
(2)相交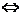
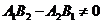 ;
;
(3)重合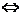
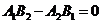 且
且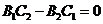 。
。
提醒:(1) 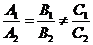 、
、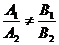 、
、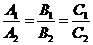 仅是两直线平行、相交、重合的充分不必要条件!为什么?(2)在解析几何中,研究两条直线的位置关系时,有可能这两条直线重合,而在立体几何中提到的两条直线都是指不重合的两条直线;(3)直线
仅是两直线平行、相交、重合的充分不必要条件!为什么?(2)在解析几何中,研究两条直线的位置关系时,有可能这两条直线重合,而在立体几何中提到的两条直线都是指不重合的两条直线;(3)直线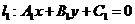 与直线
与直线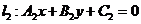 垂直
垂直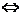
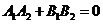 。如(1)设直线
。如(1)设直线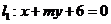 和
和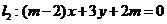 ,当
,当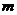 =_______时
=_______时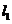 ∥
∥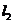 ;当
;当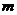 =________时
=________时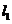
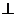
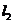 ;当
;当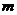 _________时
_________时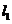 与
与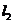 相交;当
相交;当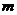 =_________时
=_________时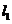 与
与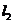 重合(答:-1;
重合(答:-1;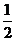 ;
;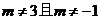 ;3);(2)已知直线
;3);(2)已知直线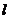 的方程为
的方程为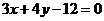 ,则与
,则与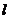 平行,且过点(-1,3)的直线方程是______(答:
平行,且过点(-1,3)的直线方程是______(答: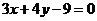 );(3)两条直线
);(3)两条直线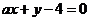 与
与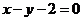 相交于第一象限,则实数
相交于第一象限,则实数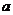 的取值范围是____(答:
的取值范围是____(答: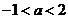 );(4)设
);(4)设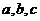 分别是△ABC中∠A、∠B、∠C所对边的边长,则直线
分别是△ABC中∠A、∠B、∠C所对边的边长,则直线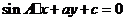 与
与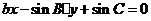 的位置关系是____(答:垂直);(5)已知点
的位置关系是____(答:垂直);(5)已知点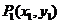 是直线
是直线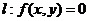 上一点,
上一点,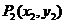 是直线
是直线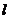 外一点,则方程
外一点,则方程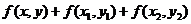 =0所表示的直线与
=0所表示的直线与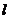 的关系是____(答:平行);(6)直线
的关系是____(答:平行);(6)直线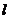 过点(1,0),且被两平行直线
过点(1,0),且被两平行直线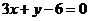 和
和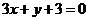 所截得的线段长为9,则直线
所截得的线段长为9,则直线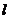 的方程是________(答:
的方程是________(答: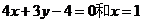 )
)
5、点到直线的距离及两平行直线间的距离:
(1)点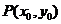 到直线
到直线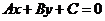 的距离
的距离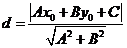 ;
;
(2)两平行线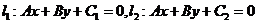 间的距离为
间的距离为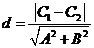 。
。
4.设直线方程的一些常用技巧:(1)知直线纵截距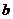 ,常设其方程为
,常设其方程为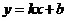 ;(2)知直线横截距
;(2)知直线横截距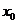 ,常设其方程为
,常设其方程为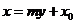 (它不适用于斜率为0的直线);(3)知直线过点
(它不适用于斜率为0的直线);(3)知直线过点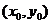 ,当斜率
,当斜率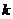 存在时,常设其方程为
存在时,常设其方程为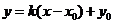 ,当斜率
,当斜率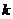 不存在时,则其方程为
不存在时,则其方程为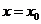 ;(4)与直线
;(4)与直线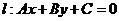 平行的直线可表示为
平行的直线可表示为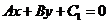 ;(5)与直线
;(5)与直线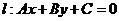 垂直的直线可表示为
垂直的直线可表示为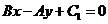 .
.
提醒:求直线方程的基本思想和方法是恰当选择方程的形式,利用待定系数法求解。
3、直线的方程:(1)点斜式:已知直线过点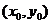 斜率为
斜率为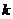 ,则直线方程为
,则直线方程为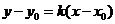 ,它不包括垂直于
,它不包括垂直于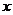 轴的直线。(2)斜截式:已知直线在
轴的直线。(2)斜截式:已知直线在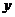 轴上的截距为
轴上的截距为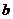 和斜率
和斜率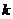 ,则直线方程为
,则直线方程为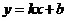 ,它不包括垂直于
,它不包括垂直于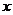 轴的直线。(3)两点式:已知直线经过
轴的直线。(3)两点式:已知直线经过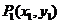 、
、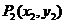 两点,则直线方程为
两点,则直线方程为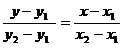 ,它不包括垂直于坐标轴的直线。(4)截距式:已知直线在
,它不包括垂直于坐标轴的直线。(4)截距式:已知直线在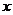 轴和
轴和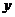 轴上的截距为
轴上的截距为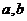 ,则直线方程为
,则直线方程为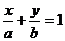 ,它不包括垂直于坐标轴的直线和过原点的直线。(5)一般式:任何直线均可写成
,它不包括垂直于坐标轴的直线和过原点的直线。(5)一般式:任何直线均可写成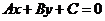 (A,B不同时为0)的形式。如(1)经过点(2,1)且方向向量为
(A,B不同时为0)的形式。如(1)经过点(2,1)且方向向量为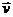 =(-1,
=(-1,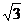 )的直线的点斜式方程是___________(答:
)的直线的点斜式方程是___________(答: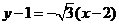 );(2)直线
);(2)直线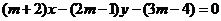 ,不管
,不管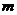 怎样变化恒过点______(答:
怎样变化恒过点______(答: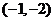 );(3)若曲线
);(3)若曲线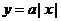 与
与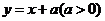 有两个公共点,则
有两个公共点,则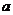 的取值范围是_______(答:
的取值范围是_______(答: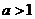 )
)
提醒:(1)直线方程的各种形式都有局限性.(如点斜式不适用于斜率不存在的直线,还有截距式呢?);(2)直线在坐标轴上的截距可正、可负、也可为0.直线两截距相等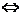 直线的斜率为-1或直线过原点;直线两截距互为相反数
直线的斜率为-1或直线过原点;直线两截距互为相反数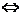 直线的斜率为1或直线过原点;直线两截距绝对值相等
直线的斜率为1或直线过原点;直线两截距绝对值相等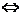 直线的斜率为
直线的斜率为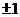 或直线过原点。如过点
或直线过原点。如过点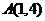 ,且纵横截距的绝对值相等的直线共有___条(答:3)
,且纵横截距的绝对值相等的直线共有___条(答:3)
2、直线的斜率:(1)定义:倾斜角不是90°的直线,它的倾斜角的正切值叫这条直线的斜率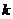 ,即
,即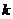 =tan
=tan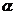 (
(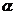 ≠90°);倾斜角为90°的直线没有斜率;(2)斜率公式:经过两点
≠90°);倾斜角为90°的直线没有斜率;(2)斜率公式:经过两点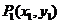 、
、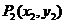 的直线的斜率为
的直线的斜率为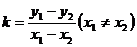 ;(3)直线的方向向量
;(3)直线的方向向量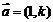 ,直线的方向向量与直线的斜率有何关系?(4)应用:证明三点共线:
,直线的方向向量与直线的斜率有何关系?(4)应用:证明三点共线: 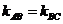 。如(1) 两条直线钭率相等是这两条直线平行的____________条件(答:既不充分也不必要);(2)实数
。如(1) 两条直线钭率相等是这两条直线平行的____________条件(答:既不充分也不必要);(2)实数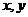 满足
满足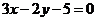 (
(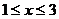 ),则
),则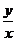 的最大值、最小值分别为______(答:
的最大值、最小值分别为______(答: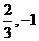 )
)
1、直线的倾斜角:(1)定义:在平面直角坐标系中,对于一条与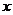 轴相交的直线
轴相交的直线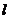 ,如果把
,如果把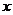 轴绕着交点按逆时针方向转到和直线
轴绕着交点按逆时针方向转到和直线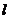 重合时所转的最小正角记为
重合时所转的最小正角记为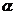 ,那么
,那么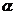 就叫做直线的倾斜角。当直线
就叫做直线的倾斜角。当直线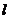 与
与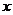 轴重合或平行时,规定倾斜角为0;(2)倾斜角的范围
轴重合或平行时,规定倾斜角为0;(2)倾斜角的范围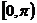 。如(1)直线
。如(1)直线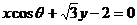 的倾斜角的范围是____(答:
的倾斜角的范围是____(答: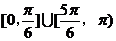 );(2)过点
);(2)过点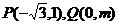 的直线的倾斜角的范围
的直线的倾斜角的范围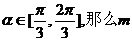 值的范围是______(答:
值的范围是______(答: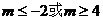 )
)
14.二次方程、二次不等式、二次函数间的联系你了解了吗?二次方程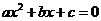 的两个根即为二次不等式
的两个根即为二次不等式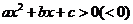 的解集的端点值,也是二次函数
的解集的端点值,也是二次函数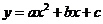 的图象与
的图象与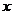 轴的交点的横坐标。如(1)不等式
轴的交点的横坐标。如(1)不等式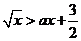 的解集是
的解集是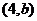 ,则
,则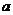 =__________(答:
=__________(答: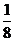 );(2)若关于
);(2)若关于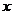 的不等式
的不等式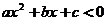 的解集为
的解集为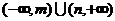 ,其中
,其中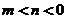 ,则关于
,则关于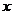 的不等式
的不等式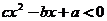 的解集为________(答:
的解集为________(答: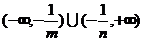 );(3)不等式
);(3)不等式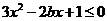 对
对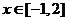 恒成立,则实数
恒成立,则实数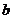 的取值范围是_______(答:
的取值范围是_______(答: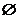 )。
)。
13.一元二次方程根的分布理论。方程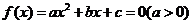 在
在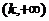 上有两根、在
上有两根、在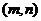 上有两根、在
上有两根、在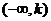 和
和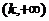 上各有一根的充要条件分别是什么?
上各有一根的充要条件分别是什么?
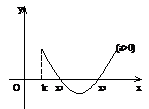 (
(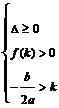 、
、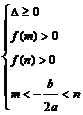 、
、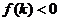 )。根的分布理论成立的前提是开区间,若在闭区间
)。根的分布理论成立的前提是开区间,若在闭区间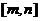 讨论方程
讨论方程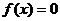 有实数解的情况,可先利用在开区间
有实数解的情况,可先利用在开区间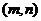 上实根分布的情况,得出结果,再令
上实根分布的情况,得出结果,再令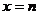 和
和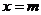 检查端点的情况.如实系数方程
检查端点的情况.如实系数方程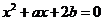 的一根大于0且小于1,另一根大于1且小于2,则
的一根大于0且小于1,另一根大于1且小于2,则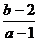 的取值范围是_________(答:(
的取值范围是_________(答:(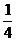 ,1))
,1))
12. 对于方程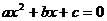 有实数解的问题。首先要讨论最高次项系数
有实数解的问题。首先要讨论最高次项系数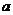 是否为0,其次若
是否为0,其次若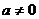 ,则一定有
,则一定有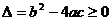 。对于多项式方程、不等式、函数的最高次项中含有参数时,你是否注意到同样的情形?如:(1)
。对于多项式方程、不等式、函数的最高次项中含有参数时,你是否注意到同样的情形?如:(1)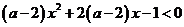 对一切
对一切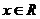 恒成立,则
恒成立,则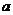 的取值范围是_______(答:
的取值范围是_______(答: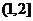 );(2)关于
);(2)关于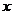 的方程
的方程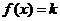 有解的条件是什么?(答:
有解的条件是什么?(答: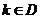 ,其中
,其中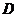 为
为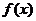 的值域),特别地,若在
的值域),特别地,若在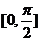 内有两个不等的实根满足等式
内有两个不等的实根满足等式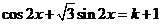 ,则实数
,则实数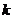 的范围是_______.(答:
的范围是_______.(答: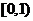 )
)
11. 一元二次不等式的解集(联系图象)。尤其当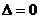 和
和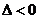 时的解集你会正确表示吗?设
时的解集你会正确表示吗?设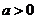 ,
,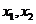 是方程
是方程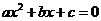 的两实根,且
的两实根,且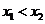 ,则其解集如下表:
,则其解集如下表:
|
|
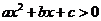 |
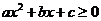 |
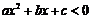 |
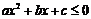 |
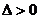 |
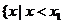 或 或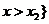 |
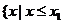 或 或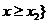 |
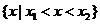 |
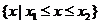 |
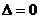 |
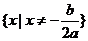 |
R |
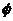 |
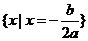 |
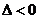 |
R |
R |
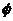 |
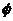 |
如解关于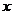 的不等式:
的不等式: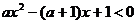 。(答:当
。(答:当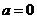 时,
时,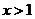 ;当
;当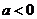 时,
时,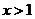 或
或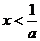 ;当
;当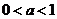 时,
时,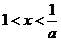 ;当
;当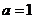 时,
时,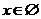 ;当
;当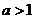 时,
时,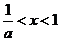 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com