
山西省太原五中2009年四月高三月考 数 学(理)
一.选择题(本题共12小题,每小题5分,共60分;在每小题给出的四个选项中,
1.设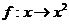 是集合A到集合B的映射,若
是集合A到集合B的映射,若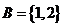 则
则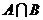 等于( )
等于( )
A.  B.
B.
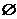 C.
C.
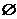 或
或 D.
D. 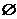 或
或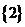
2.与复数 的积为1的复数的虚部为
( )
的积为1的复数的虚部为
( )
A. 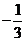 B.
B.
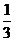 C.
C.
 D.1
D.1
3.直线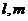 与平面
与平面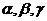 满足
满足 ,
, ,那么必有 (
)
,那么必有 (
)
A. 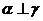 且
且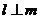 B.
B. 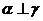 且
且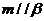
C. 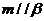 且
且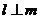 D.
D. 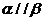 且
且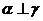
4.甲、乙、丙、丁、戊5人站成一排,要求甲乙均不与丙相邻,不同排法种数有 ( )
A. 72
B
5.若直线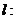 mx+ny=4和圆O:
mx+ny=4和圆O: 没有交点,则过点(m,n)的直线与椭圆
没有交点,则过点(m,n)的直线与椭圆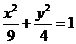 的交点个数为(
)
的交点个数为(
)
A.至多一个 B.2个 C.1个 D.0个
6.若函数 的导数是
的导数是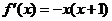 则函数
则函数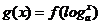 (0<a<1)的单调递减区间是(
)
(0<a<1)的单调递减区间是(
)
A. 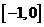 B.
B.  ,
, 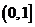 C.
C. 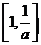 D.
D. 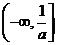 ,
,
 7. 点
7. 点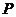 从点
从点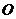 出发,按逆时针方向沿周长为
出发,按逆时针方向沿周长为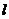 的图形运动一周,
的图形运动一周,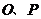 两点连线的距离
两点连线的距离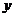 与点
与点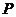 走过的路程
走过的路程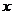 的函数关系如图,那么点
的函数关系如图,那么点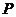 所走的图形是( )
所走的图形是( )
 |
8.四面体A-BCD的四个顶点都在半径为2的球上.且AB,AC,AD两两垂直,则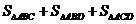 的最大值为 ( )
的最大值为 ( )
A. 8
B. 
9. 函数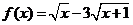 的最大值为
的最大值为 ( )
( )
A.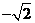 B.
B. 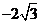 C.
C. 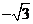 D .
D . 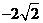
10.已知点P是椭圆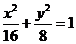
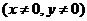 上的动点,
上的动点, 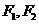 为椭圆的两个焦点,O是坐标原点,若M是
为椭圆的两个焦点,O是坐标原点,若M是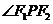 的角平分线上一点且
的角平分线上一点且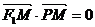 ,则
,则
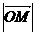 的取值范围为( )
的取值范围为( )
A. 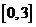 B.
B.
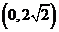 C
C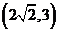 D.
D. 
11.双曲线 的左、右焦点分别为
的左、右焦点分别为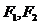 ,点
,点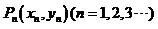 在其右支上,且满足
在其右支上,且满足 ,
,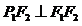 ,则
,则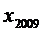 的值是 ( )
的值是 ( )
A.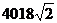 B.
B.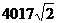 C.
C.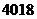 D.
D.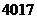
12.数列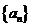 满足
满足
 且
且 …
…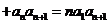 对任何的正整数成立,则
对任何的正整数成立,则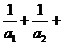 …
… 的值为 ( )
的值为 ( )
A. 5032 B.
二.填空题(本题共4小题,每题5分,共20分)
13.二项式 展开式中所有无理系数之和为
展开式中所有无理系数之和为
14.已知 ,
,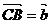 ,
, =2 当
=2 当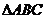 的面积最大时,
的面积最大时,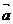 与
与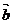 的夹角为
的夹角为
15.已知曲线C:  与函数
与函数 和
和 (a>0且
(a>0且 )的图象在第一象限的交点分别为
)的图象在第一象限的交点分别为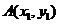 ,
, ,则
,则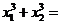
16.实系数一元二次方程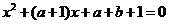 的两个实根为
的两个实根为 ,若0<
,若0<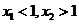 ,则
,则 的取值范围为
的取值范围为
三.解答题(本题共6小题,第17题10分,其余每题12分,共70分)
17.(本小题满分10分)
已知△ABC的面积S满足3≤S≤3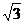 且
且 的夹角为
的夹角为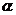 ,
,
(Ⅰ)求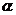 的取值范围;
的取值范围;
(Ⅱ)求 的最小值。
的最小值。
18.(本小题满分12分)在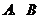 两只口袋中均有
两只口袋中均有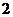 个红球和
个红球和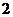 个白球,先从
个白球,先从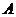 袋中任取
袋中任取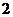 个球转放到
个球转放到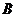 袋中,再从
袋中,再从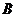 袋中任取一个球转放到
袋中任取一个球转放到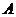 袋中,结果
袋中,结果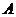 袋中恰有
袋中恰有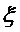 个红球.
个红球.
(1)求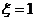 时的概率;(2)求随机变量
时的概率;(2)求随机变量 的分布列及期望.www.1010jiajiao.co
的分布列及期望.www.1010jiajiao.co
19.(本小题满分12分)
已知三棱锥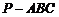 中,
中,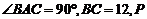 在底面
在底面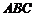 上的射影
上的射影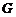 为
为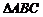 的重心,且
的重心,且 .
.
 (Ⅰ)求
(Ⅰ)求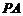 与底面
与底面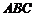 所成的角的大小;
所成的角的大小;
(Ⅱ)当二面角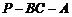 的大小最小时,
的大小最小时,
求三棱锥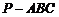 的体积.
的体积.
20.(本小题满分12分)
已知函数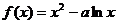 在(1,2
在(1,2 是增函数,
是增函数, 在(0,1)为减函数.
在(0,1)为减函数.
(1)求 、
、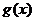 的表达式;
的表达式;
(2)求证:当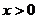 时,方程
时,方程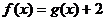 有唯一解;
有唯一解;
(3)当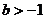 时,若
时,若 在
在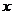 ∈(0,1
∈(0,1 内恒成立,求
内恒成立,求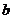 的取值范围.
的取值范围.
21.(本小题满分12分)
在直角坐标平面中,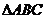 的两个顶点
的两个顶点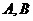 的坐标分别为
的坐标分别为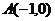 ,
, ,平面内两点
,平面内两点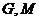 同时满足下列条件:
同时满足下列条件:
① ;②
;②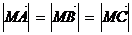 ;③
;③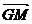 ∥
∥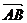 .
.
(1)求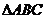 的顶点
的顶点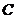 的轨迹方程;
的轨迹方程;
(2)过点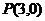 的直线
的直线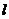 与(1)中轨迹交于不同的两点
与(1)中轨迹交于不同的两点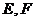 ,求
,求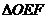 面积的最大值.
面积的最大值.
22.(本小题满分12分)
已知数列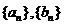 满足关系:
满足关系: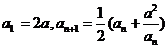 ,
,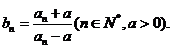
(1)求证:数列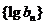 是等比数列;
是等比数列;
(2)证明: ;
;
(3)设 是数列
是数列 的前n项和,当
的前n项和,当 时,
时, 是否有确定的大小关系?若有,加以证明;若没有,请说明理由。
是否有确定的大小关系?若有,加以证明;若没有,请说明理由。
太 原 五 中
2008―2009学年度第二学期月考 (4月)
高三数学(理)答卷纸
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
13 ; 14 .;
二、填空题(每小题5分)
15. ; 16 。
三.解答题(本题共6小题,第17题10分,其余每题12分,共70分)
17.
18.
 19.
19.
20.
(21、22题请写在背面,请标清题号。)
高三数学(理)答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
A
C
B
C
C
A
D
B
C
B
二、填空题(每小题5分)
13. ; 14.
; 14.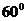 ; 15. 2
; 16.
; 15. 2
; 16. 。
。
三.解答题(本题共6小题,第17题10分,其余每题12分,共70分)
17.解 (Ⅰ)由题意知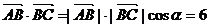
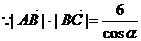
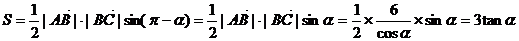 ……………………3分
……………………3分
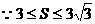
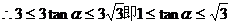 ……………………4分
……………………4分
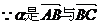 的夹角,
的夹角,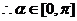
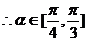 ……………………5分
……………………5分
(Ⅱ)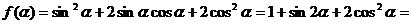
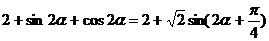 ……………………8分
……………………8分
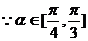
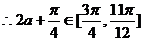
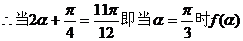 有最小值。
有最小值。
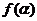 的最小值是
的最小值是 ……………………10分
……………………10分
18.解:(1)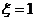 表示经过操作以后
表示经过操作以后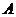 袋中只有一个红球,有两种情形出现
袋中只有一个红球,有两种情形出现
①先从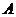 中取出
中取出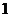 红和
红和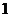 白,再从
白,再从 中取一白到
中取一白到 中
中
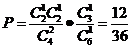
②先从 中取出
中取出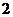 红球,再从
红球,再从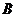 中取一红球到
中取一红球到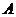 中
中
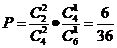
 …………………………………………6分
…………………………………………6分
(2)同(1)中计算方法可知:
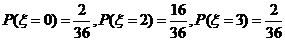
 |
 的概率分布列
的概率分布列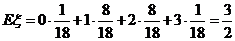 ……………………………12分
……………………………12分
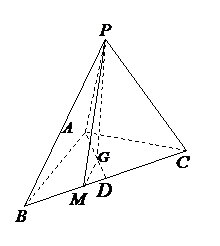 19.解:(Ⅰ)如图,连
19.解:(Ⅰ)如图,连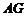 并延长交
并延长交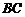 于点
于点 ,依题意知,
,依题意知,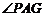 就是
就是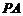 与底面
与底面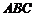 所成的角,且
所成的角,且 为
为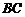 的中点.∴
的中点.∴ ,
,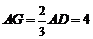 .
.
在 中,
中, ,∴
,∴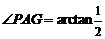 ,故
,故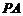 与底面
与底面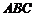 所成的角
所成的角 .…………………5分
.…………………5分
(Ⅱ)过点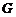 作
作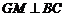 于
于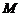 ,连
,连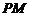 ,则
,则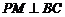 ,∴
,∴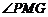 为二面角
为二面角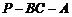 的平面角.
的平面角.
在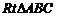 中,斜边
中,斜边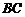 上的高为
上的高为 ,∴
,∴ .
.
在 中,
中,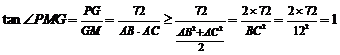 .∴二面角
.∴二面角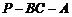 的最小值为
的最小值为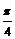 ,当且仅当
,当且仅当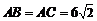 .∴
.∴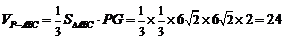 .…………12分
.…………12分
20.解(1)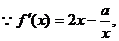 依题意
依题意
又∵ ,依题意
,依题意

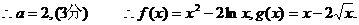 …………………4分
…………………4分
(2)由(1)可知,原方程为
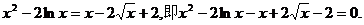
设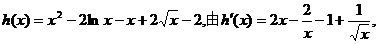
令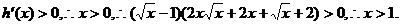
令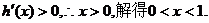
由
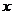
(0,1)
1
(1,+∞)
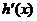
-
0
+
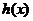
递减
0
递增
即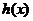 在
在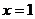 处有一个最小值0,即当
处有一个最小值0,即当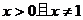 时,
时,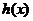 >0,
>0, 只有一个解.
只有一个解.
即当x>0时,方程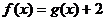 有唯一解.
…………………8分
有唯一解.
…………………8分
(3)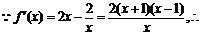 当
当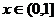 时
时 为减函数,其最小值为1.
为减函数,其最小值为1.
令 恒成立.
恒成立.
∴函数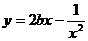 在
在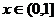 为增函数,其最大值为2b-1,
为增函数,其最大值为2b-1,
依题意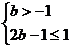 ,解得
,解得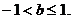 为所求范围. …………………12分
为所求范围. …………………12分
21.解:(1)设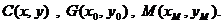
 ,
,
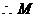 点在线段
点在线段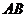 的中垂线上.由已知
的中垂线上.由已知 . …………1分
. …………1分
又 ∥
∥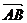 ,
,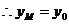 .又
.又 ,
,
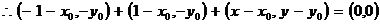 ,
,
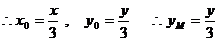 . ………………………………3分
. ………………………………3分
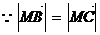 ,
,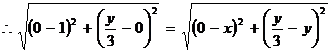 ,
,
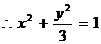
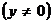 ,
,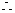 顶点
顶点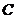 的轨迹方程为
的轨迹方程为
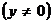 . ……………… …5分
. ……………… …5分
(2)设直线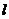 方程为:
方程为: ,
,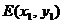 ,
,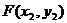 ,
,
由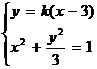 消去
消去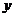 得:
得: ①
①
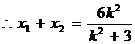 ,
,  .
.
由方程①知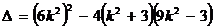 >
>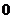 ,
,
 <
<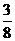 ,
, ,
, <
< <
<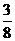 . …………………………………8分
. …………………………………8分
而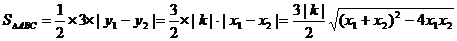
 .………………………10分
.………………………10分
令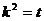 ,则
,则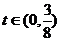 ,
,
 .记
.记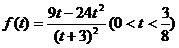 ,
,
求导易得当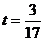 时有
时有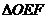 面积的最大值
面积的最大值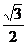 . ……………………12分
. ……………………12分
22.解:(1)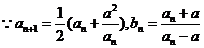
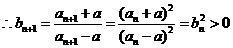
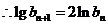
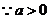
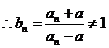
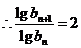 故
故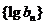 是等比数列。 ……………………4分
是等比数列。 ……………………4分
(2)
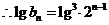
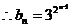
由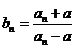 及:
及: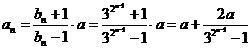
 ……………………8分
……………………8分
(3)当 时,
时,
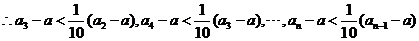
相加得: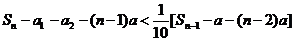
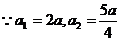
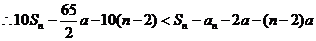
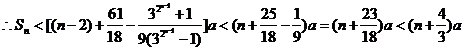
故 时,
时,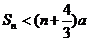 . ……………………12分
. ……………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com