
上海市2009年高考模拟试题汇编
圆锥曲线
一、填空题
1、(2009上海青浦区)已知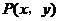 是椭圆
是椭圆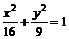 上的一个动点,则
上的一个动点,则
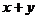 的最大值是 .
的最大值是 .
5
2、(2009闵行三中模拟)已知 为双曲线
为双曲线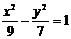 的右顶点,F是双曲线的右焦点,则|AF|=_______。
的右顶点,F是双曲线的右焦点,则|AF|=_______。
1
3、(2009冠龙高级中学3月月考)以椭圆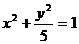 中心为顶点,右顶点为焦点的抛物线的标准方程为_____________。
中心为顶点,右顶点为焦点的抛物线的标准方程为_____________。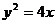
4、(2009上海普陀区)设联结双曲线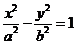 与
与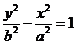 (
( ,
,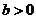 )的
)的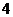 个顶点的四边形面积为
个顶点的四边形面积为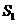 ,联结其
,联结其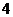 个焦点的四边形面积为
个焦点的四边形面积为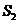 ,则
,则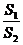 的最大值为
.
的最大值为
.
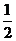
5、(2009上海十四校联考)以原点为顶点,x轴为对称轴且焦点在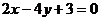 上的抛物线方程是
上的抛物线方程是
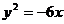 。
。
二、解答题
1、(2009上海十四校联考)我们知道,判断直线与圆的位置关系可以用圆心到直线的距离进行判别,那么直线与椭圆的位置关系有类似的判别方法吗?请同学们进行研究并完成下面问题
(1)设F1、F2是椭圆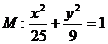 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线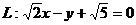 的距离分别为d1、d2,试求d1?d2的值,并判断直线L与椭圆M的位置关系
的距离分别为d1、d2,试求d1?d2的值,并判断直线L与椭圆M的位置关系
(2)设F1、F2是椭圆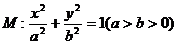 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线
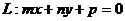 (m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1?d2的值
(m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1?d2的值
(3)试写出一个能判断直线与椭圆的位置关系的充要条件,并证明
(4)将(3)中得出的结论类比到其它曲线,请同学们给出自己研究的有关结论(不必证明)
解:(1)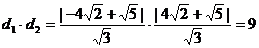 ; ………………2分
; ………………2分
联立方程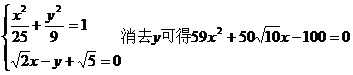 ; …………3分
; …………3分
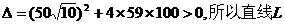 与椭圆M相交 …………4分
与椭圆M相交 …………4分
(2)联立方程组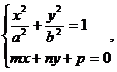
消去
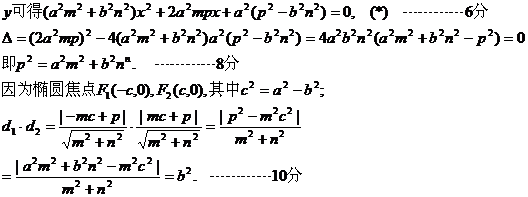
(3)设F1、F2是椭圆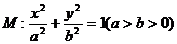 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线
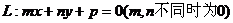 的距离分别为d1、d2,且F1、F2在直线L的同侧那么直线L与椭圆相交的充要条件为:
的距离分别为d1、d2,且F1、F2在直线L的同侧那么直线L与椭圆相交的充要条件为: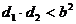 ;直线L与椭圆M相切的充要条件为:
;直线L与椭圆M相切的充要条件为: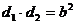 ;直线L与椭圆M相离的充要条件为:
;直线L与椭圆M相离的充要条件为: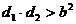 ……14分
……14分
证明:由(2)得,直线L与椭圆M相交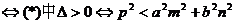
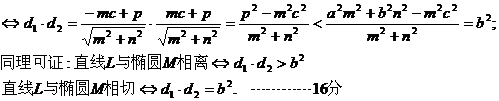
命题得证
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
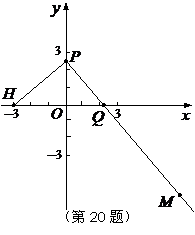 (4)可以类比到双曲线:设F1、F2是双曲线
(4)可以类比到双曲线:设F1、F2是双曲线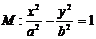 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线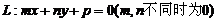 距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为:
距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为: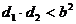 ;直线L与双曲线M相切的充要条件为:
;直线L与双曲线M相切的充要条件为: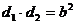 ;直线L与双曲线M相离的充要条件为:
;直线L与双曲线M相离的充要条件为: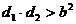
………………20分
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
2、(2009上海卢湾区4月模考)如图,已知点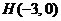 ,动点
,动点 在
在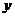 轴上,点
轴上,点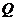
在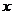 轴上,其横坐标不小于零,点
轴上,其横坐标不小于零,点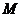 在直线
在直线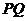 上,
上,
且满足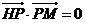 ,
, .
.
(1)当点 在
在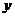 轴上移动时,求点
轴上移动时,求点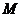 的轨迹
的轨迹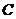 ;
;
(2)过定点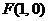 作互相垂直的直线
作互相垂直的直线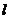 与
与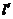 ,
,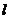 与
与
(1)中的轨迹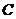 交于
交于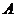 、
、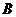 两点,
两点,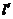 与(1)中的轨迹
与(1)中的轨迹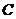 交于
交于 、
、 两点,求四边形
两点,求四边形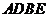 面积
面积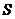 的最小值;
的最小值;
(3)(在下列两题中,任选一题,写出计算过程,并求出结果,若同时选做两题,
则只批阅第②小题,第①题的解答,不管正确与否,一律视为无效,不予批阅):
① (解答本题,最多得6分)将(1)中的曲线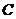 推广为椭圆:
推广为椭圆: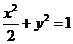 ,并
,并
将(2)中的定点取为焦点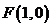 ,求与(2)相类似的问题的解;
,求与(2)相类似的问题的解;
② (解答本题,最多得9分)将(1)中的曲线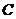 推广为椭圆:
推广为椭圆: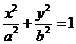 ,并
,并
将(2)中的定点取为原点,求与(2)相类似的问题的解.
解:(1)设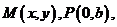
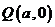
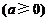 ,易知
,易知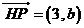 ,
,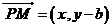 ,
, ,由题设
,由题设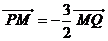 ,
,
得 其中
其中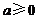 ,从而
,从而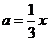 ,
,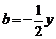 ,且
,且 ,
,
又由已知 ,得
,得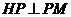 ,
,
当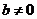 时,
时, ,此时
,此时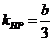 ,得
,得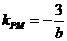 ,
,
又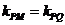 ,故
,故 ,
, ,即
,即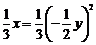 ,
,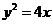
 ,
,
当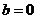 时,点
时,点 为原点,
为原点,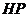 为
为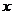 轴,
轴, 为
为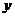 轴,点
轴,点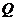 也为原点,从而点
也为原点,从而点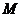 也为原点,因此点
也为原点,因此点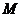 的轨迹
的轨迹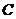 的方程为
的方程为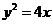 ,它表示以原点为顶点,以
,它表示以原点为顶点,以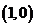 为焦点的抛物线;
(4分)
为焦点的抛物线;
(4分)
(2)由题设,可设直线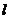 的方程为
的方程为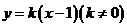 ,直线
,直线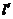 的方程为
的方程为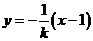 ,
,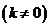 ,又设
,又设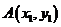 、
、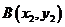 ,
,
则由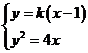 ,消去
,消去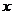 ,整理得
,整理得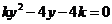 ,
,
故 ,同理
,同理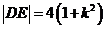 ,
(7分)
,
(7分)
则 ,当且仅当
,当且仅当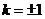 时等号成立,因此四边形
时等号成立,因此四边形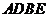 面积
面积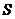 的最小值为
的最小值为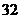 . (9分)
. (9分)
(3)① 当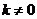 时可设直线
时可设直线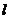 的方程为
的方程为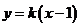 ,
,
由 ,得
,得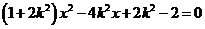 ,
,
故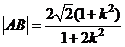 ,
,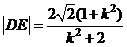 ,
(12分)
,
(12分)
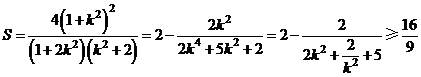 ,
,
当且仅当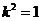 时等号成立. (14分)
时等号成立. (14分)
当 时,易知
时,易知 ,
,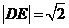 ,得
,得 ,故当且仅当
,故当且仅当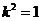 时四边形
时四边形 面积
面积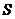 有最小值
有最小值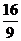 .
(15分)
.
(15分)
② 由题设,可设直线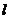 的方程为
的方程为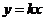 ,当
,当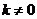 时,由
时,由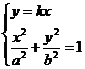 ,
,
消去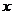 ,整理得
,整理得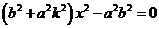 ,得
,得 ,
,
同理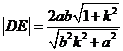 ,
(12分)
,
(12分)
则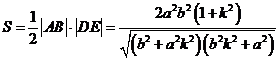 ,其中
,其中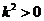 ,
,
若令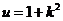 ,则由
,则由
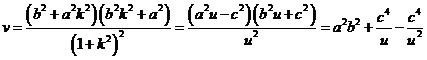
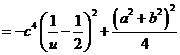 ,其中
,其中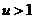 ,即
,即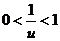 ,故当且仅当
,故当且仅当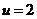 ,即
,即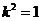 时,
时,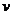 有最大值
有最大值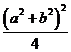 ,由
,由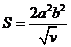 ,得
,得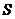 有最小值
有最小值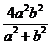 ,故当且仅当
,故当且仅当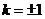 时,四边形
时,四边形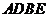 面积
面积 有最小值为
有最小值为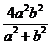 . (17分)
. (17分)
又当 时,
时,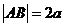 ,
,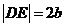 ,此时
,此时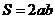 ,由
,由 ,得当且仅当
,得当且仅当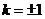 时,四边形
时,四边形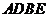 面积
面积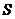 有最小值为
有最小值为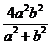 . (18分)
. (18分)
3、(2009上海八校联考)已知双曲线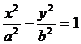 的渐近线方程为
的渐近线方程为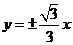 ,左焦点为F,过
,左焦点为F,过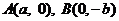 的直线为
的直线为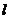 ,原点到直线
,原点到直线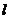 的距离是
的距离是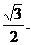
(1)求双曲线的方程;
(2)已知直线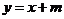 交双曲线于不同的两点C,D,问是否存在实数
交双曲线于不同的两点C,D,问是否存在实数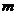 ,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由
,使得以CD为直径的圆经过双曲线的左焦点F。若存在,求出m的值;若不存在,请说明理由
解:(1)∵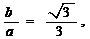
 2分
2分
原点到直线AB: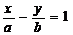 的距离,
的距离,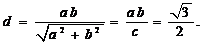
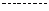 4分
4分
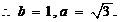 故所求双曲线方程为
故所求双曲线方程为 
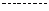 6分
6分
(2)把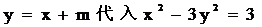 中消去y,整理得
中消去y,整理得 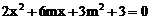 .
.  8分
8分
设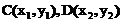 ,则
,则
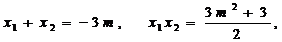
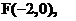
因为以CD为直径的圆经过双曲线的左焦点F,所以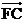
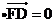 ,
, 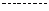 10分
10分
可得 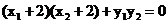 把
把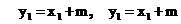 代入,
代入,
解得: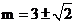
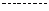 13分
13分
解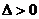 ,得
,得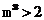 ,
,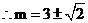 满足
满足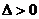 ,
,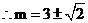
 14分
14分
4、(2009上海奉贤区模拟考)已知:点P与点F(2,0)的距离比它到直线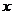 +4=0的距离小2,若记点P的轨迹为曲线C。
+4=0的距离小2,若记点P的轨迹为曲线C。
(1)求曲线C的方程。
(2)若直线L与曲线C相交于A、B两点,且OA⊥OB。求证:直线L过定点,并求出该定点的坐标。
(3)试利用所学圆锥曲线知识参照(2)设计一个与直线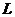 过定点有关的数学问题,并解答所提问题。
过定点有关的数学问题,并解答所提问题。
(1)解法(A):点P与点F(2,0)的距离比它到直线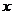 +4=0的距离小2,所以点P与点F(2,0)的距离与它到直线
+4=0的距离小2,所以点P与点F(2,0)的距离与它到直线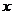 +2=0的距离相等。 ----(1分)
+2=0的距离相等。 ----(1分)
由抛物线定义得:点 在以
在以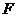 为焦点直线
为焦点直线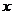 +2=0为准线的抛物线上, ----(1分)
+2=0为准线的抛物线上, ----(1分)
抛物线方程为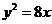 。 ----(2分)
。 ----(2分)
解法(B):设动点 ,则
,则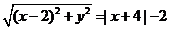 。当
。当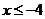 时,
时, ,化简得:
,化简得: ,显然
,显然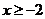 ,而
,而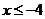 ,此时曲线不存在。当
,此时曲线不存在。当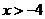 时,
时,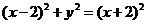 ,化简得:
,化简得: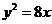 。
。
(2)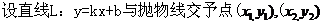 ,
,
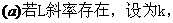 ,
,
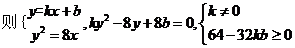 ,
----(1分)
,
----(1分)
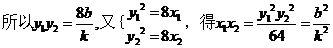 ,
,
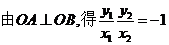 ,即
,即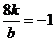 ,
, , ----(2分)
, ----(2分)
直线为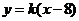 ,所以
,所以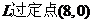 ----(1分)
----(1分)
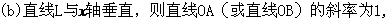
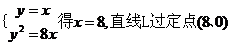 ----(1分)
----(1分)
由(a)(b)得:直线恒过定点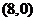 。
----(1分)
。
----(1分)
1、(逆命题)如果直线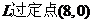 ,且与抛物线
,且与抛物线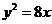 相交于A、B两点,O为坐标原点。求证:OA⊥OB (评分:提出问题得1分,解答正确得1分)
相交于A、B两点,O为坐标原点。求证:OA⊥OB (评分:提出问题得1分,解答正确得1分)
(若,求证: ?
? =0,得分相同)
=0,得分相同)
2、(简单推广命题)如果直线L与抛物线 =2px(p>0)相交于A、B两点,且OA⊥OB。求证:直线L过定点(2p,0)
=2px(p>0)相交于A、B两点,且OA⊥OB。求证:直线L过定点(2p,0)
或:它的逆命题(评分:提出问题得2分,解答正确得1分)
3、(类比)
3.1(1)如果直线L与椭圆 +
+ =1(a>b>0)相交于A、B两点,M是其右顶点,当MA⊥MB。求证:直线L过定点(
=1(a>b>0)相交于A、B两点,M是其右顶点,当MA⊥MB。求证:直线L过定点( ,0)
,0)
3.1(2)如果直线L与椭圆 +
+ =1(a>b>0)相交于A、B两点,M是其左顶点,当MA⊥MB。求证:直线L过定点(
=1(a>b>0)相交于A、B两点,M是其左顶点,当MA⊥MB。求证:直线L过定点( ,0)
,0)
3.1(3)或它的逆命题
3.2(1)如果直线L与双曲线 -
- =1(a>0,b>0)相交于A、B两点,M是其右顶点,当MA⊥MB。求证:直线L过定点(
=1(a>0,b>0)相交于A、B两点,M是其右顶点,当MA⊥MB。求证:直线L过定点( ,0)(a≠b)
,0)(a≠b)
3.2(2)如果直线L与双曲线 -
- =1(a>0,b>0)相交于A、B两点,M是其左顶点,当MA⊥MB。求证:直线L过定点(
=1(a>0,b>0)相交于A、B两点,M是其左顶点,当MA⊥MB。求证:直线L过定点( ,0)(a≠b)
,0)(a≠b)
3.2(3)或它的逆命题
(评分:提出问题得3分,解答正确得3分)
4、(再推广)
直角顶点在圆锥曲线上运动
如:如果直线L与抛物线 =2px(p>0)相交于A、B两点,P是抛物线上一定点(
=2px(p>0)相交于A、B两点,P是抛物线上一定点( ,
, ),且PA⊥PB。求证:直线L过定点(
),且PA⊥PB。求证:直线L过定点( +2p,-
+2p,- )
)
(评分:提出问题得4分,解答正确得3分)
5、(再推广)
如果直线L与抛物线 =2px(p>0)相交于A、B两点,P是抛物线上一定点(
=2px(p>0)相交于A、B两点,P是抛物线上一定点( ,
, ),PA与PB的斜率乘积是常数m。求证:直线L过定点(
),PA与PB的斜率乘积是常数m。求证:直线L过定点( -
-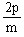 ,-
,- )
)
(评分:提出问题得5分,解答正确得4分)
或 ?
?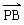 为常数
为常数
顶点在圆锥曲线上运动并把直角改为一般定角或OA与OB的斜率乘积是常数或 ?
? 为常数
为常数
5、(2009冠龙高级中学3月月考)双曲线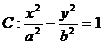 上一点
上一点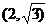 到左,右两焦点距离的差为2.
到左,右两焦点距离的差为2.
(1)求双曲线的方程;
(2)设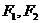 是双曲线的左右焦点,
是双曲线的左右焦点, 是双曲线上的点,若
是双曲线上的点,若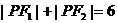 ,
,
求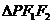 的面积;
的面积;
(3)过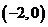 作直线
作直线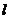 交双曲线
交双曲线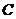 于
于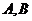 两点,若
两点,若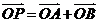 ,是否存在这样的直线
,是否存在这样的直线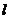 ,使
,使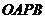 为矩形?若存在,求出
为矩形?若存在,求出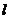 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
(1)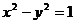
(2) 妨设 在第一象限,则
在第一象限,则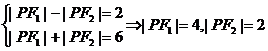
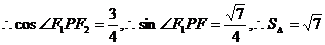
(3)若直线斜率存在,设为 ,代入
,代入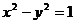
得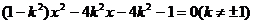
若平行四边形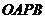 为矩形,则
为矩形,则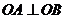

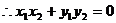
 无解
无解
若直线垂直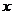 轴,则
轴,则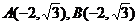 不满足.
不满足.
故不存在直线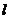 ,使
,使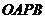 为矩形.
为矩形.
6、(2009上海青浦区)已知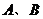 是抛物线
是抛物线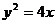 上的相异两点.
上的相异两点.
(1)设过点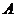 且斜率为-1的直线
且斜率为-1的直线 ,与过点
,与过点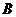 且斜率1的直线
且斜率1的直线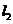 相交于点P(4,4),求直线AB的斜率;
相交于点P(4,4),求直线AB的斜率;
(2)问题(1)的条件中出现了这样的几个要素:已知圆锥曲线G,过该圆锥曲线上的
相异两点A、B所作的两条直线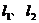 相交于圆锥曲线G上一点;结论是关于直线AB的斜率的值.请你对问题(1)作适当推广,并给予解答;
相交于圆锥曲线G上一点;结论是关于直线AB的斜率的值.请你对问题(1)作适当推广,并给予解答;
(3)线段AB(不平行于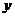 轴)的垂直平分线与
轴)的垂直平分线与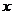 轴相交于点
轴相交于点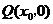 .若
.若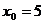 ,试用线段AB中点的纵坐标表示线段AB的长度,并求出中点的纵坐标的取值范围.
,试用线段AB中点的纵坐标表示线段AB的长度,并求出中点的纵坐标的取值范围.
(1)由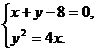 解得
解得 ;由
;由 解得
解得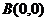 .
.
由点斜式写出两条直线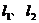 的方程,
的方程,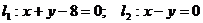 ,
,
所以直线AB的斜率为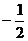 . ……4分
. ……4分
(2)推广的评分要求分三层
一层:点P到一般或斜率到一般,或抛物线到一般(3分,问题1分、解答2分)
例:1.已知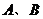 是抛物线
是抛物线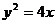 上的相异两点.设过点
上的相异两点.设过点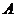 且斜率为-1的直线
且斜率为-1的直线 ,与过点
,与过点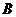 且斜率为1的直线
且斜率为1的直线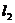 相交于抛物线
相交于抛物线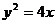 上的一定点P
上的一定点P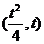 ,求直线AB的斜率;
,求直线AB的斜率;
2.已知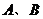 是抛物线
是抛物线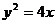 上的相异两点.设过点
上的相异两点.设过点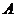 且斜率为-k 1的直线
且斜率为-k 1的直线 ,与过点
,与过点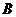 且斜率为k的直线
且斜率为k的直线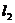 相交于抛物线
相交于抛物线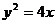 上的一点P(4,4),求直线AB的斜率;
上的一点P(4,4),求直线AB的斜率;
3.已知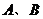 是抛物线
是抛物线 上的相异两点.设过点
上的相异两点.设过点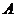 且斜率为-1的直线
且斜率为-1的直线 ,与过点
,与过点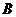 且斜率为1的直线
且斜率为1的直线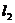 相交于抛物线
相交于抛物线 上的一定点P
上的一定点P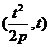 ,求直线AB的斜率; AB的斜率的值.
,求直线AB的斜率; AB的斜率的值.
二层:两个一般或推广到其它曲线(4分,问题与解答各占2分)
例:4.已知点R是抛物线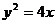 上的定点.过点P作斜率分别为
上的定点.过点P作斜率分别为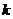 、
、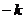 的两条直线
的两条直线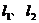 ,分别交抛物线于A、B两点,试计算直线AB的斜率.
,分别交抛物线于A、B两点,试计算直线AB的斜率.
三层:满分(对抛物线,椭圆,双曲线或对所有圆锥曲线成立的想法.)(7分,问题3分、解答4分)
例如:5.已知抛物线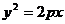 上有一定点P,过点P作斜率分别为
上有一定点P,过点P作斜率分别为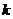 、
、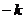 的两条直线
的两条直线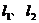 ,分别交抛物线于A、B两点,试计算直线AB的斜率.
,分别交抛物线于A、B两点,试计算直线AB的斜率.
过点P( ),斜率互为相反数的直线可设为
),斜率互为相反数的直线可设为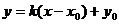 ,
,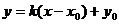 ,其中
,其中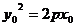 。
。
由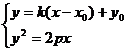 得
得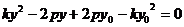 ,所以
,所以

同理,把上式中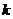 换成
换成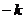 得
得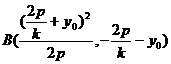 ,所以
,所以
当P为原点时直线AB的斜率不存在,当P不为原点时直线AB的斜率为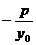 。
。
(3)(理)点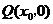 ,设
,设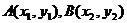 ,则
,则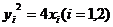 .
.
设线段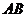 的中点是
的中点是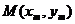 ,斜率为
,斜率为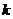 ,则
,则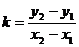 =
=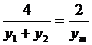 .12分
.12分
所以线段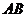 的垂直平分线
的垂直平分线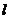 的方程为
的方程为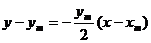 ,
,
又点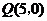 在直线
在直线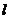 上,所以
上,所以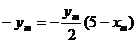 ,而
,而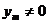 ,于是
,于是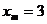 .
……13分
.
……13分
(斜率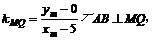
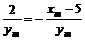 ,则
,则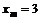 --------------------------------13分)
--------------------------------13分)
线段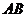 所在直线的方程为
所在直线的方程为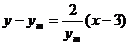 ,
……14分
,
……14分
代入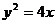 ,整理得
,整理得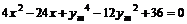 ……15分
……15分
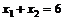 ,
,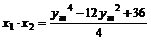 。设
。设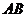 线段长为
线段长为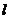 ,则
,则
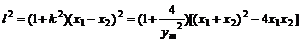 =
=
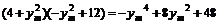 ……16分
……16分
因为 ,所以
,所以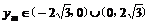 ……18分
……18分
即: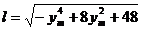 .(
.(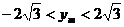 )
)
(文)设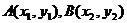 ,则
,则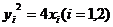 .
……13分
.
……13分
设线段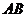 的中点是
的中点是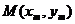 ,斜率为
,斜率为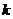 ,则
,则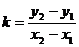 =
=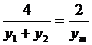 ,……15分
,……15分
线段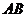 的垂直平分线
的垂直平分线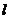 的方程为
的方程为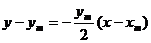 , ……17分
, ……17分
又点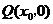 在直线
在直线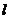 上,所以
上,所以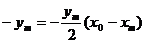 ,
,
而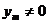 ,于是
,于是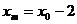 .故线段AB中点的横坐标为
.故线段AB中点的横坐标为 . ……18分
. ……18分
7、(2009上海十校联考)已知等轴双曲线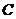 的两个焦点
的两个焦点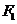 、
、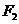 在直线
在直线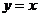 上,线段
上,线段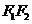 的中点是坐标原点,且双曲线经过点
的中点是坐标原点,且双曲线经过点 .
.
(1)
若已知下列所给的三个方程中有一个是等轴双曲线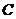 的方程:①
的方程:①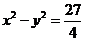 ;②
;②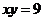 ;③
;③ .请确定哪个是等轴双曲线
.请确定哪个是等轴双曲线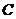 的方程,并求出此双曲线的实轴长;
的方程,并求出此双曲线的实轴长;
(2)
 现要在等轴双曲线
现要在等轴双曲线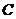 上选一处
上选一处 建一座码头,向
建一座码头,向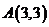 、
、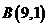 两地转运货物.经测算,从
两地转运货物.经测算,从 到
到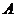 、从
、从 到
到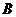 修建公路的费用都是每单位长度
修建公路的费用都是每单位长度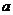 万元,则码头应建在何处,才能使修建两条公路的总费用最低?
万元,则码头应建在何处,才能使修建两条公路的总费用最低?
(3)
如图,函数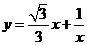 的图像也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
的图像也是双曲线,请尝试研究此双曲线的性质,你能得到哪些结论?(本小题将按所得到的双曲线性质的数量和质量酌情给分)
【解】(1)双曲线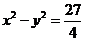 的焦点在
的焦点在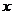 轴上,所以①不是双曲线
轴上,所以①不是双曲线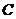 的方程……1分
的方程……1分
双曲线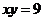 不经过点
不经过点 ,所以②不是双曲线
,所以②不是双曲线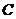 的方程
…… 2分
的方程
…… 2分
所以③ 是等轴双曲线
是等轴双曲线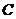 的方程
…… 3分
的方程
…… 3分
等轴双曲线 的焦点
的焦点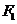 、
、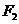 在直线
在直线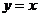 上,所以双曲线的顶点也在直线
上,所以双曲线的顶点也在直线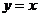 上,
…… 4分
上,
…… 4分
联立方程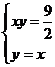 ,解得双曲线
,解得双曲线 的两顶点坐标为
的两顶点坐标为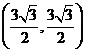 ,
,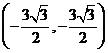 ,所以双曲线
,所以双曲线 的实轴长为
的实轴长为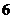 …… 5分
…… 5分
(2)
所求问题即为:在双曲线 求一点
求一点 ,使
,使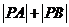 最小.
最小.
首先,点 应该选择在等轴双曲线的
应该选择在等轴双曲线的 中第一象限的那一支上 …… 6分
中第一象限的那一支上 …… 6分
等轴双曲线的 的长轴长为
的长轴长为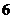 ,所以其焦距为
,所以其焦距为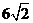
又因为双曲线的两个焦点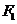 、
、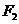 在直线
在直线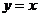 上,线段
上,线段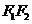 的中点是原点,所以
的中点是原点,所以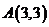 是
是 的一个焦点,
…… 7分
的一个焦点,
…… 7分
设双曲线的另一个焦点为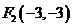 ,由双曲线的定义知:
,由双曲线的定义知: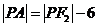
所以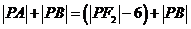 ,要求
,要求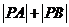 的最小值,只需求
的最小值,只需求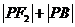 的最小值
…… 8分
的最小值
…… 8分
直线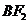 的方程为
的方程为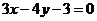 ,所以直线
,所以直线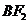 与双曲线
与双曲线 在第一象限的交点为
在第一象限的交点为 …… 9分
…… 9分
所以码头应在建点
 处,才能使修建两条公路的总费用最低 …… 10分
处,才能使修建两条公路的总费用最低 …… 10分
(3)① 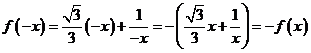 ,此双曲线是中心对称图形,对称中心是原点
,此双曲线是中心对称图形,对称中心是原点 ;
…… 1分
;
…… 1分
② 渐近线是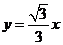 和
和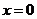 .当
.当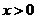 时,当
时,当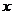 无限增大时,
无限增大时,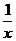 无限趋近于
无限趋近于 ,
,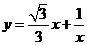 与
与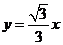 无限趋近;当
无限趋近;当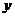 无限增大时,
无限增大时,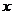 无限趋近于
无限趋近于 .
…… 2分
.
…… 2分
③ 双曲线的对称轴是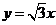 和
和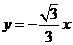 .
…… 3分
.
…… 3分
④ 双曲线的顶点为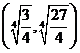 ,
,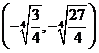 ,实轴在直线
,实轴在直线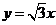 上,实轴长为
上,实轴长为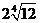 …… 4分
…… 4分
⑤虚轴在直线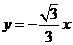 ,虚轴长为
,虚轴长为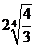 …… 5分
…… 5分
⑥焦点坐标为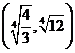 ,
,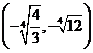 ,焦距
,焦距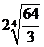 …… 6分
…… 6分
说明:(i)若考生能把上述六条双曲线的性质都写出,建议此小题给满分8分
(ii)若考生未能写全上述六条双曲线的性质,但是给出了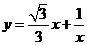 的一些函数性质(诸如单调性、最值),那么这些函数性质部分最多给1分
的一些函数性质(诸如单调性、最值),那么这些函数性质部分最多给1分
8、(2009上海九校联考) 如图,已知椭圆
如图,已知椭圆 的焦点和上顶点分别为
的焦点和上顶点分别为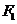 、
、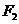 、
、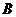 ,
,
我们称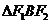 为椭圆
为椭圆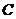 的特征三角形.如果两个椭圆的
特征三角形是相似的,
的特征三角形.如果两个椭圆的
特征三角形是相似的,
则称这两个椭圆是“相似椭圆”,且三角形的相似比即为 椭圆的相似比.
(1)已知椭圆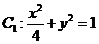 和
和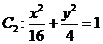 ,
,
判断 与
与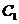 是否相似,
是否相似,
如果相似则求出 与
与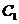 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)已知直线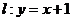 ,与椭圆
,与椭圆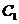 相似且半短轴长为
相似且半短轴长为 的椭圆
的椭圆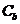 的方程,
的方程,
在椭圆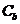 上是否存在两点
上是否存在两点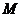 、
、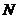 关于直线
关于直线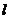 对称,
对称,
若存在,则求出函数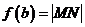 的解析式.
的解析式.
(3)根据与椭圆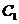 相似且半短轴长为
相似且半短轴长为 的椭圆
的椭圆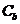 的方程,提出你认为有价值的
的方程,提出你认为有价值的
相似椭圆之间的三种性质(不需证明);
解:
解:(1)椭圆 与
与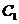 相似. ………2分
相似. ………2分
因为 的特征三角形是腰长为4,底边长为
的特征三角形是腰长为4,底边长为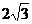 的等腰三角形,
的等腰三角形,
而椭圆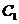 的特征三角形是腰长为2,底边长为
的特征三角形是腰长为2,底边长为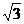 的等腰三角形,
的等腰三角形,
因此两个等腰三角形相似,且相似比为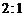 ……… 6分
……… 6分
(2)椭圆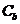 的方程为:
的方程为: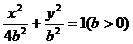 .
………8分
.
………8分
假定存在,则设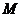 、
、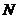 所在直线为
所在直线为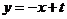 ,
,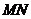 中点为
中点为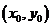 .
.
则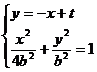
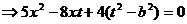 .
………10分
.
………10分
所以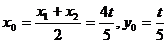 .
.
中点在直线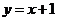 上,所以有
上,所以有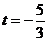 . ………12分
. ………12分
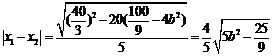 .
.
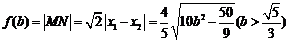 . ………14分
. ………14分
(3)椭圆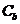 的方程为:
的方程为: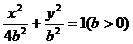 .
.
两个相似椭圆之间的性质有: 写出一个给2分
① 两个相似椭圆的面积之比为相似比的平方;
② 分别以两个相似椭圆的顶点为顶点的四边形也相似,相似比即为椭圆的相似比;
③ 两个相似椭圆被同一条直线所截得的线段中点重合;
过原点的直线截相似椭圆所得线段长度之比恰为椭圆的相似比. ………20分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com