
题目列表(包括答案和解析)
3.平衡条件的推论
⑴物体在多个共点力作用下处于平衡状态,则其中的一个力与余下的力的合力等大反向。
⑵几个力构成平衡力,其中任意几个力的合力和其余力的合力构成平衡力。
|

对于共点力作用下物体的平衡,不要认为只有静止才是平衡状态,匀速直线运动也是物体的平衡状态.因此,静止的物体一定平衡,但平衡的物体不一定静止.还需注意,不要把速度为零和静止状态相混淆,静止状态是物体在一段时间内保持速度为零不变,其加速度为零,而物体速度为零可能是物体静止,也可能是物体做变速运动中的一个状态,加速度不为零。由此可见,静止的物体速度一定为零,但速度为零的物体不一定静止.因此,静止的物体一定处于平衡状态,但速度为零的物体不一定处于静止状态。
总之,共点力作用下的物体只要物体的加速度为零,它一定处于平衡状态,只要物体的加速度不为零,
它一定处于非平衡状态
|

2.平衡条件:共点力作用下物体的平衡条件是所受合外力为零,即F合=0
把一个力分解成两个互相垂直的分力,这种分解方法称为正交分解法。
用正交分解法求合力的步骤:
①首先建立平面直角坐标系,并确定正方向
②把各个力向x轴、y轴上投影,但应注意的是:与确定的正方向相同的力为正,与确定的正方向相反的为负,这样,就用正、负号表示了被正交分解的力的分力的方向
③求在x轴上的各分力的代数和Fx合和在y轴上的各分力的代数和Fy合
④求合力的大小 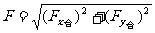
合力的方向:tanα=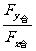 (α为合力F与x轴的夹角)
(α为合力F与x轴的夹角)
力的正交分解法是把作用在物体上的所有力分解到两个互相垂直的坐标轴上,分解最终往往是为了求合力(某一方向的合力或总的合力)。
|

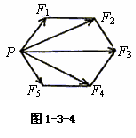
例1.如图1-3-4所示.有五个力作用于一点P,构成一个正六边形的两个邻边和三条对角线,设 F3=10N,则这五个力的合力大小为( )
 A.10(2+
A.10(2+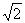 )N
)N
B. 20N
C.30N
D.0
解析:由平行四边形定则
 得选项C对
得选项C对
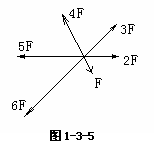
变式训练1:六个共点力的大小分别为F、2F、3F、4F、5F、6F,相邻两个力之间夹角均为60º,如图1-3-5所示,则它们的合力大小是____,方向____。
解析:6F 方向与原来5F方向相同
例2.如图1-4-6所示,小木块放在倾角为α的斜面上,受到一个水平力F(F≠0)的作用处于静止,如图1-4-7所示,则小木块受到斜面的支持力和摩擦力的合力的方向与竖直向上的方向的夹角β可能是( )
A. β=0
B. 合力的方向向右上方,β<α
C. 合力的方向向左上方,β<α
D. 合力的方向向左上方,β>α
|
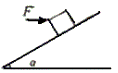
解析::物体受到重力g,支持力FN,外力F和静摩擦力Ff四个力的作用 ,由于小木块处在平衡状态,可知支持力力静摩擦和的合力方向一定与重力和推力的合力方向相反,由于F的大小未知,故其与G的合力方向可能落在斜面的垂线MN的左下方,(F较小对应图中F1)这时摩擦力和支持力的合力方向就落在MN与竖直线的夹角内,即β< ,故D正确;F与G的合力方向也可能落在斜面的垂线MN的右上方,(F较大对应图中的F2)这时摩擦力和支持力的合力方向就落在MN与竖直线的夹角外,即β>
,故D正确;F与G的合力方向也可能落在斜面的垂线MN的右上方,(F较大对应图中的F2)这时摩擦力和支持力的合力方向就落在MN与竖直线的夹角外,即β>
变式训练2:如图1-3-7所示:物体静止于光滑的水平面M上,力F作用于O点,现欲用F1和F2两个力共同作用于O点取代F的单独作用,F1方向如图虚线所示,则另一个力F2的大小最小为 。
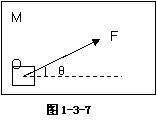
解析:另一个力F2的大小最小为Fsinθ
第4课时 共点力作用下物体的平衡(一)
|

物体的平衡
1.平衡状态:静止或匀速直线运动状态
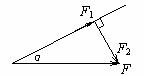
(1)当已知合力F的大小、方向及一个分力F1的方向时,另一个分力F2取最小值的条件是两分力垂直。如图1-3-2所示,F2的最小值为:F2min=F sinα
|
|
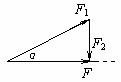 (2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2取最小值的条件是:所求分力F2与合力F垂直,如图1-3-3所示,F2的最小值为:F2min=F1sinα
(2)当已知合力F的方向及一个分力F1的大小、方向时,另一个分力F2取最小值的条件是:所求分力F2与合力F垂直,如图1-3-3所示,F2的最小值为:F2min=F1sinα
(3)当已知合力F的大小及一个分力F1的大小时,另一个分力F2取最小值的条件是:已知大小的分力F1与合力F同方向,F2的最小值为|F-F1
3.几种有条件的力的分解
(1)已知合力与两个分力的方向,求两个分力的大小时,有唯一解。
(2)已知合力与一个分力的大小和方向,求另一个分力的大小和方向时,有唯一解。
(3)已知合力与两个分力的大小,求两个分力的方向时,其分解不唯一。
(4)已知合力F与一个分力F2的大小和另一个分力F1的方向,求这个分力F2的方向和另一个分力F1的大小时,其分解方法可能唯一,也可能不唯一。这时则有如下的几种可能情况:
① 当F>F2>Fsinθ时,有两个解
② 当F2=Fsinθ时,有唯一解
③ 当F2<Fsinθ时,无解
④ 当F2>F时,有唯一解
|

2.分力和合力的关系
合力F可能比分力大,也可能比分力小,还可能等于某个分力的大小,或同时等于两个分力的大小。
3.同一直线上矢量的合成可转为代数法,即规定某一方向为正方向。与正方向相同的物理量用正号代入.相反的用负号代入,然后求代数和,最后结果的正、负体现了方向,但有些物理量虽也有正负之分,但不能认为是矢量,最后结果的正负也不表示方向如:功、重力势能、电势能、电势等。
2.矢量和标量的根本区别在于它们遵从不同的运算法则:标量用代数法;矢量用平行四边形定则或三角形定则。
矢量的合成与分解都遵从平行四边形定则(可简化成三角形定则)。平行四边形定则实质上是一种等效替换的方法。一个矢量(合矢量)的作用效果和另外几个矢量(分矢量)共同作用的效果相同,就可以用这一个矢量代替那几个矢量,也可以用那几个矢量代替这一个矢量,而不改变原来的作用效果。
1.将物理量区分为矢量和标量体现了用分类方法研究物理问题的思想。
3.在复习时我们应当特别明确一个问题, 力的合成和分解是由受力分析到建立力学方程的过程所采取的一种手段, 是处理复杂受力情况的一种方法。合成和分解不是机械的、死板的,在有明确的目的前提下要灵活运用。
合成与分解是为了研究问题的方便而引人的一种方法.用合力来代替几个力时必须把合力与各分力脱钩,即考虑合力则不能考虑分力,同理在力的分解时只考虑分力而不能同时考虑合力。
|

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com