
题目列表(包括答案和解析)
5.若x,y是正数,则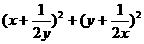 的最小值是 ( )
的最小值是 ( )
A.3 B.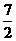 C.4 D.
C.4 D.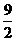
解: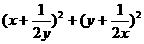 ≥2(x+
≥2(x+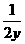 )(y+
)(y+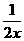 )≥8
)≥8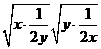 =4当且仅当
=4当且仅当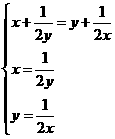 ,得x=y=
,得x=y=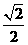 时等号成立,选(C)
时等号成立,选(C)
4.已知A(3,1),B(6,1),C(4,3),D为线段BC的中点,则向量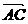 与
与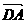 的夹角为 ( )
的夹角为 ( )
A.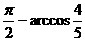 B.
B.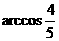 C.
C.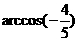 D.-
D.-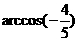
解:∵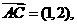 D(5,2),
D(5,2),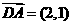 ,
,
∴cos(180°-∠DAC)=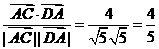 ,∴∴∠DAC=
,∴∴∠DAC=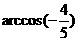 ,即向量
,即向量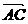 与
与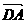 的夹角为
的夹角为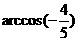 ,选(C)
,选(C)
3.若函数 是定义在R上的偶函数,在
是定义在R上的偶函数,在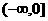 上是减函数,且
上是减函数,且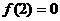 ,则使得
,则使得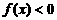 的x的取值范围是 ( )
的x的取值范围是 ( )
A.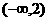 B.
B.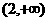 C.
C.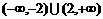 D.(-2,2)
D.(-2,2)
解:∵函数 是定义在R上的偶函数,在
是定义在R上的偶函数,在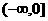 上是减函数,且
上是减函数,且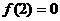 ,∴f(-2)=0, 在
,∴f(-2)=0, 在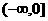 上
上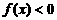 的x的取值范围是
的x的取值范围是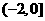 ,又由对称性
,又由对称性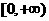 ,∴在R上fx)<0仰x的取值范围为(-2,2),选(D)
,∴在R上fx)<0仰x的取值范围为(-2,2),选(D)
2.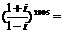 ( )
( )
A.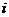 B.-
B.-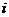 C.
C. D.-
D.-
解:∵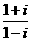 =-i,∴
=-i,∴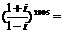 (-i)2005=
(-i)2005=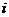 ,选(A)
,选(A)
1.圆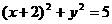 关于原点(0,0)对称的圆的方程为 ( )
关于原点(0,0)对称的圆的方程为 ( )
A.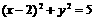 B.
B.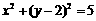
C.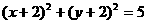 D.
D.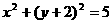
解:∵圆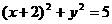 的圆心(-2,0)关于原点对称的点为(2,0),∴圆
的圆心(-2,0)关于原点对称的点为(2,0),∴圆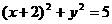 关于原点对称的圆为(x-2)2+y2=5,选(A).
关于原点对称的圆为(x-2)2+y2=5,选(A).
20.已知函数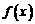 和
和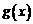 的图象关于原点对称,且
的图象关于原点对称,且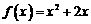 .
.
(Ⅰ)求函数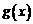 的解析式;
的解析式;
(Ⅱ)解不等式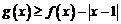 ;
;
(Ⅲ)若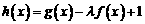 在
在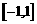 上是增函数,求实数
上是增函数,求实数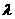 的取值范围.
的取值范围.
解:解:(Ⅰ)设函数y=f(x)的图象上任一点Q(xqλ,yq关于原点的对称点(x,y),
则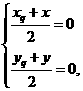 即
即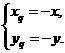 ∵点Qxq,yq)在函数f(x)的图象上,
∵点Qxq,yq)在函数f(x)的图象上,
∴-y=-x2+2x.,故g(x)=-x2+2x
(Ⅱ)由g(x)≥f(x)-|x-1|可得2x2-|x-1|≤0,当x≥1时,2x2-x+1≤0,此时不等式无解,
当x<1时,2x2+x-1≤0,∴-1≤x≤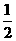 ,因此,原不等式的解集为[-1,
,因此,原不等式的解集为[-1,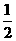 ]
]
(Ⅲ)h(x)=-(1+λ)x2+2(1-λ)x+1
① 当λ=-1时,h(x)=4x+1在[-1,1]上是增函数,∴λ=-1
② 当λ≠-1时,对称轴的方程为x=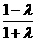 .
.
(i)
当λ<-1时, 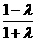 ≤-1,解得λ<-1.
≤-1,解得λ<-1.
(ii)
当λ>-1时, 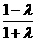 ≥-1,解得-1<λ≤0.
≥-1,解得-1<λ≤0.
综上,λ≤0
19.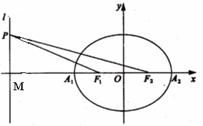 如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
(Ⅰ)求椭圆的方程;
(Ⅱ)若点P为l上的动点,求∠F1PF2最大值.
解:(Ⅰ)设椭圆的方程为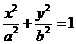 (a>0,b>0),半焦距为c,则|MA1|=
(a>0,b>0),半焦距为c,则|MA1|=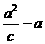 ,|A1F1|=a-c
由题意,得
,|A1F1|=a-c
由题意,得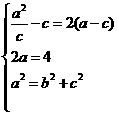 ∴a=2,b=
∴a=2,b=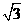 ,c=1.
,c=1.
故椭圆的方程为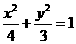
(Ⅱ)设P(-4,y0),y0≠0,
∴只需求tan∠F1PF2的最大值即可.
设直线PF1的斜率k1=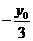 ,直线PF2的斜率k2=
,直线PF2的斜率k2=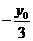 ,
,
∵0<∠F1PF2<∠PF1M<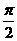 ,∴∠F1PF2为锐角.
,∴∠F1PF2为锐角.
∴tan∠F1PF2=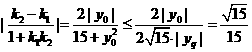
当且仅当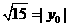 ,即|y0|=
,即|y0|=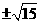 时,tan∠F1PF2取到最大值此时∠F1PF2最大,∴
时,tan∠F1PF2取到最大值此时∠F1PF2最大,∴
∠F1PF2的最大值为arctan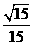 .
.
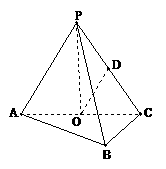
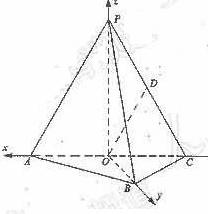
18.如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=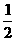 PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
PA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(Ⅰ)求证:OD∥平面PAB;
(Ⅱ) 求直线OD与平面PBC所成角的大小.
解:解法一
(Ⅰ)∵O、D分别为AC、PC的中点:∴OD∥PA,又AC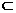 平面PAB,∴OD∥平面PAB.
平面PAB,∴OD∥平面PAB.
(Ⅱ)∵AB⊥BC,OA=OC,∴OA=OC=OB,又∵OP⊥平面ABC,∴PA=PB=PC.
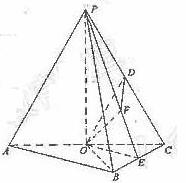
取BC中点E,连结PE,则BC⊥平面POE,作OF⊥PE于F,连结DF,则OF⊥平面PBC
∴∠ODF是OD与平面PBC所成的角.
又OD∥PA,∴PA与平面PBC所成角的大小等于∠ODF.
在Rt△ODF中,sin∠ODF=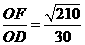 ,∴PA与平面PBC所成角为arcsin
,∴PA与平面PBC所成角为arcsin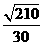
解法二:
∵OP⊥平面ABC,OA=OC,AB=BC,∴OA⊥OB,OA⊥OP,OB⊥OP.
以O为原点,射线OP为非负x轴,建立空间坐标系O-xyz如图),设AB=a,则A(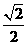 a,0,0).
a,0,0).
B(0, 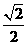 a,0),C(-
a,0),C(-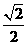 a,0,0).设OP=h,则P(0,0,h).
a,0,0).设OP=h,则P(0,0,h).
(Ⅰ)∵D为PC的中点,∴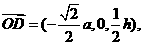 又
又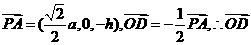 ∥
∥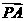 ,
,
∴OD∥平面PAB.
(Ⅱ)∵k=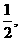 则PA=2a,∴h=
则PA=2a,∴h=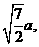 ∴
∴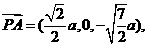 可求得平面PBC的法向量
可求得平面PBC的法向量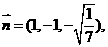
∴cos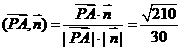 .
.
设PA与平面PBC所成角为θ,刚sinθ=|cos(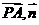 )|=
)|=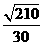 .
.
∴PA与平面PBC所成的角为arcsin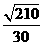 .
.
17.袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是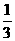 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,共摸5次.(i)恰好有3次摸到红球的概率;(ii)第一次、第三次、第五次摸到红球的概率.
(Ⅱ) 若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是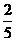 ,求p的值.
,求p的值.
解:(Ⅰ)(i)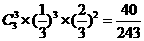
(ii)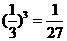
(iii)设袋子A中有m个球,则袋子B中有2m个球,
由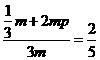 ,得p=
,得p=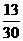 .
.
16.已知实数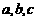 成等差数列,
成等差数列,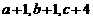 成等比数列,且
成等比数列,且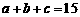 ,求
,求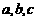 .
.
解: 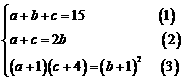
由(1)(2)两式,解得b=5,将c=10-a代入(3),整理得a2-13a+22=0,解得a=2或a=11.
故a=2,b=5,c=11或a=11,b=5,c=-1.经验算,上述两组数符合题意.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com