
题目列表(包括答案和解析)
2、 切线长定理包含两个结论,如图(1)所示,PA、PB切⊙O于点A、B,则有: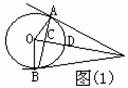
(1)“切线长相等”,即PA=PB。
(2)“圆心和这点的连线平分两切线的夹角”,即:PO平分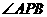 ;
;
根据PA=PB,PO平分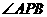 ,可得点A、B关于直线OP对称,从而有OP垂直平分AB、
,可得点A、B关于直线OP对称,从而有OP垂直平分AB、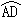 =
=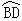 以及
以及 ∽
∽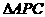 ∽
∽ 等结论,由此可得,切线长定理是证明线段相等、角相等、弧相等、线段成比例,垂直关系的重要依据。
等结论,由此可得,切线长定理是证明线段相等、角相等、弧相等、线段成比例,垂直关系的重要依据。
1、 “切线长”是切线上一条线段的长度,具有数量的特征;而“切线”是一条直线,它是向两方无限延展的,不可以度量长度。
3、 能结合具体图形,准确地表述相交弦定理、切割线定理及其推论的题设和结论,并能应用它们解有关的计算和证明题,会作两条线段的比例中项。
2、 理解弦切角的概念,掌握弦切角定理及其推论,并会运用它们解决有关问题,通过弦切角定理的证明,进一步了解分情况证明数学命题的思想和方法。
1、 理解切线长的概念,掌握切线长定理并会运用它解决有关问题。
2.(1)A; (2)D (3)D (4)D (5)B
1.
(1)相离,相切; (2)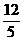 ,大于
,大于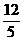 ;
;
(3)
相切或相交; (4) ,90,相切;
,90,相切;
(5)30,120,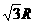 ; (6)
; (6)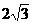 ; (7)115
; (7)115
(8)
1:2; (9)15,60,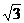 ,1,
,1, 。
。
2. 选择题
(1) 设⊙O半径为 ,点O到直线I的距离为
,点O到直线I的距离为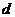 ,若⊙O与
,若⊙O与 至多只有一个公共点,则
至多只有一个公共点,则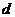 与
与 的关系为( )
的关系为( )
(A) 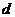 ≥
≥ (B)
(B)
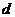 <
< (C)
(C)
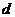 ≤
≤ (D)
(D)
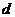 =
=
(2) 等腰△ABC的腰AB=AC=4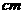 ,若以A为圆心,2
,若以A为圆心,2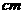 为半径的圆与BC相切,则∠BAC的度数为( )
为半径的圆与BC相切,则∠BAC的度数为( )
(A) 30O (B) 60O (C) 90O (D) 120O
(3) 下列直线中能判定为圆的切线的是( )
(A) 与圆有公共点的直线。
(B) 垂直于圆的半径的直线。
(C) 过圆的半径的外端的直线。
(D) 到圆心的距离等于该圆的半径的直线。
(4) AB是⊙O的切线,在下列给出的条件中,能判定AB⊥CD的是( )
(A) AB与⊙O相切于直线CD上的点C。
(B) CD经过圆心O。 (C) CD是直线。
(D) AB与⊙O相切于C,过圆心O。
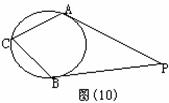
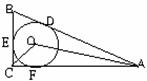
(5) 如图(10),PA、PB分别切⊙O于A、B,∠P=70O,则∠C( )
(A) 70O (B)55O (C)110O (D)140O
1. 填空题:
(1)
已知圆的直径为13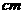 ,直线与圆心的距离为
,直线与圆心的距离为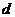 ,当
,当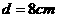 时,直线与圆
;当
时,直线与圆
;当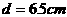 时,直线与圆 。
时,直线与圆 。
(2)
R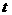 △ABC中,∠C=90O,AC=3
△ABC中,∠C=90O,AC=3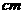 ,BC=4
,BC=4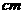 ,则以C为圆心,
,则以C为圆心,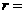
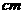 为半径的圆与AB相切;以C为圆心,
为半径的圆与AB相切;以C为圆心,
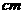 为半径的圆与AB相交。
为半径的圆与AB相交。
(3) 若直线与圆的公共点个数不小于1,则直线与圆的位置关系是 。
(4) 如图(7),A为⊙O的半径OC的延长线上一点,且CA=OC,弦BC=OC,则BC= OA,∠OBA= O ,BA与⊙O的位置关系是 。
图(7)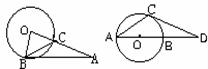 图(8)
图(8)
(5) 如图(8),已知AB是⊙O的直径,延长AB到D,使BD=OB,DC切⊙O于C,则∠D= O,∠C= O。若⊙O的半径为R,则AC= 。
(6)
两个同心圆的半径分别为1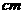 和2
和2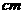 ,大圆的弦AB与小圆相切,则AB= 。
,大圆的弦AB与小圆相切,则AB= 。
(7) 已知I为△ABC的内心,∠B=50O,则∠AIC= 。
(8) 等边三角形内切圆半径与外切圆半径之比是 。
(9)
如图(9),⊙O内切于R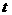 △ABC,∠C=90O,D、E、F为切点,若∠AOC=120O,则∠OAC= O,∠B= O,若AB=2
△ABC,∠C=90O,D、E、F为切点,若∠AOC=120O,则∠OAC= O,∠B= O,若AB=2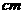 ,△ABC的外接圆半径=
,△ABC的外接圆半径= 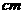 ,内切圆半径=
,内切圆半径=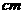 。
。
例1.
已知:如图(1)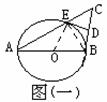 AB是⊙O的直径,CB⊥AB,AC交⊙O于E,D是的BC的中点,
AB是⊙O的直径,CB⊥AB,AC交⊙O于E,D是的BC的中点,
求证:直线DE是⊙O的切线。
证明:连结OE、BE,
∵AB是⊙O的直径,∴∠AEB=90O,
∴BE⊥AC,则∠BEC=90O,
又∵D是BC的中点,
∴DE=BD= BC,∴∠DBE=∠DEB
BC,∴∠DBE=∠DEB
∵OE=OB ∴∠OBE=∠OEB
因此:∠DBE+∠OBE=∠DEB+∠OEB
即:∠OED=∠OBD
∵BC⊥AB 即:∠OBD=90O
∴∠OED=90O
则DE是⊙O的切线。
评析:(1) 此例是由直径、圆周角、直角三角形斜边上的中线、切线的判定等知识构成的命题。(2) 证一条直线是圆的切线,常用的两个判定方法是:直线过圆上一已知点时,作过这点的半径转证直线垂直于这条半径;直线和圆的公共点的位置未知时,过圆心作到直线的距离,转证此距离等于圆的半径。此例显然用的是第一种方法。(3)此题的分析思路:要证DE是圆的切线,而E在圆上,据圆的切线的定义则E是切点,所以应连结OE,转证DE⊥OE。
例2. 已知:如图(2)所示,在直角梯形ABCD中,AD⊥CD于D,BC⊥CD于D,且AD+CB=AB,以斜腰AB为直径作⊙O,
求证:CD是⊙O的切线。
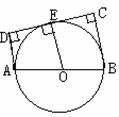 图(2)
图(2)
分析:要证CD是⊙O的切线,切点在什么位置呢?无法判定,因此应该用证明切线的第二种方法,作圆心到直线的距离OE,转而证OE等于圆的半径。
证明:过O作OE⊥CD于E,
∵AD⊥CD,BC⊥CD
∴AD||OE||BC
∵O是AB中点,则E是CD中点。
∴OE是梯形ABCD的中位线,
∴OE= (AD+BC)
(AD+BC)
又∵AD+BC=AB
∴OE= AB。
AB。
则DC是⊙O的切线。
例3. 如图(3)所示,在直角梯形ABCD中,∠A=∠B=90O,E为AB上的一点,ED平分∠ADC,EC平分∠BCD。
求证:以AB为直径的圆与DC相切。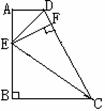 图(3)
图(3)
分析:要证以AB为直径的圆与DC相切,只需证AB的中点到DC的距离等于 AB。
AB。
证明:过点E作EF⊥CD于F。
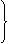 ED平分∠ADC
ED平分∠ADC
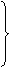
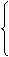
 DA⊥EA于A ÞEA=EF E为AB中点
DA⊥EA于A ÞEA=EF E为AB中点
EF⊥DF于F Þ
同理可证:EF=EB
EF= AB
AB
Þ以AB为直径的圆与CD相切。
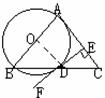
例4. 如图(3)所示,已知△ABC中,以AB为直径作⊙O交BC于D,过D作⊙O的切线FE,交AC于E,且AE⊥DE。
求证:AB=AC
 图(4)
图(4)
证明:连结OD
∵DE切⊙O于D,则OD⊥DE
∵AE⊥DE, ∴OD∥AC 则∠C=∠ODB
∵OB=OD ∴∠B=∠ODC
∴∠B=∠C 则AB=AC
例5.
已知:如图(5)所示,△ABC是⊙O的内接三角形,∠BAC的平分线交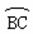 于D,过D的切线分别交AB、AC的延长线于E、F,
于D,过D的切线分别交AB、AC的延长线于E、F,
求证:BC||EF
证明:连结OD
∵EF切⊙O于D, ∴EF⊥OD
∵AD平分∠BAC ∴∠BAD=∠CAD
则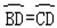
由垂径定理,知:OD⊥BC
∴BC∥EF
注:此证法运用切线的性质比较灵活巧妙,只要在已知切线时用垂直方法的意识强,则不难想到。
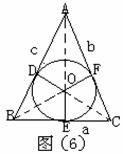
例6.
如图(6)所示,△ABC三边长为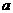 ,
,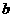 ,
,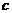 ,面积为S,内切圆⊙O的半径为
,面积为S,内切圆⊙O的半径为 ,⊙O与△ABC的三边相切于D、E、F。
,⊙O与△ABC的三边相切于D、E、F。
求证: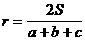
分析:要证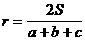 ,只需证:
,只需证: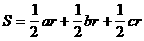 。
。
证明:连结OA、OB、OC
∵⊙O切△ABC的三边于D、E、F
∴OD⊥AB,OE⊥BC,OF⊥AC
∴S△AOB= OD·AB=
OD·AB=

同理可得:S△BOC=
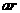 S△AOC=
S△AOC=

∴S=S△AOB+S△BOC+S△AOC=
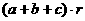
∴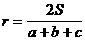
注:若∠C=90O,则有: 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com