
题目列表(包括答案和解析)
20、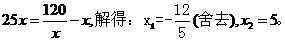
新房均价为2千元,年新房销售总额为10亿元。
19、1)
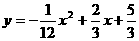

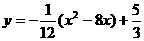

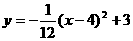
(2) 抛物线的顶点坐标为
抛物线的顶点坐标为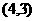
 铅球在运行过程中到达最高点时离地面的距离为3米
铅球在运行过程中到达最高点时离地面的距离为3米
当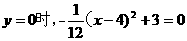 解得:
解得: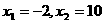

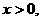
 取
取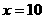
 这个学生投铅球的成绩是10米
这个学生投铅球的成绩是10米
18、⑴ 依题意,可建立的函数关系式为:
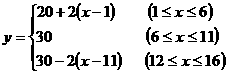 ;即
;即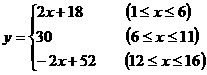
⑵ 设销售利润为W,则W=售价-进价
故W=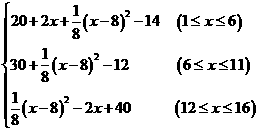
化简得W=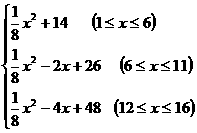
① 当W=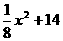 时,∵
时,∵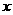 ≥0,函数
≥0,函数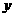 随着
随着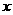 增大而增大,∵1≤
增大而增大,∵1≤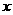 ≤6
≤6
∴当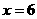 时,W有最大值,最大值=18.5
时,W有最大值,最大值=18.5
② 当W=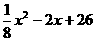 时,∵W=
时,∵W=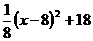 ,当
,当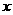 ≥8时,函数
≥8时,函数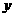 随
随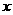
增大而增大
∴在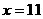 时,函数有最大值为
时,函数有最大值为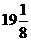
③当W=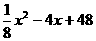 时,∵W=
时,∵W=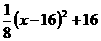 ,∵12≤
,∵12≤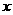 ≤16,当
≤16,当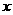 ≤16时,函数
≤16时,函数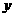 随
随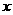 增大而减小,
增大而减小,
∴在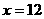 时,函数有最大值为18
时,函数有最大值为18
综上所述,当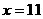 时,函数有最大值为18
时,函数有最大值为18
17、(1)延长MP交AF于点H,则△BHP为
等腰直角三角形.BH=PH=130-x
DM=HF=10-BH=10-(130-x)=x-120
则 y=PM·EM=x·[100-(x-120)]=-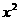 +220x
+220x
由 0≤PH≤10
得 120≤x≤130 因为抛物线y=-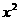 +220x的对称轴为x=110,开口向下.
+220x的对称轴为x=110,开口向下.
所以,在120≤x≤130内,当x=120时,y=-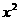 +220x取得最大值.
+220x取得最大值.
其最大值为 y=12000 (㎡)
(2)设有a户非安置户到安置区内建房,政府才能将30户移民农户全部安置.
由题意,得
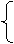 30×100+120a≤12000×50%
30×100+120a≤12000×50%
30×4+(12000-30×100-120a)×0.01+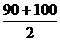 ×10×0.02≤150+3a
×10×0.02≤150+3a
解得 18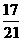 ≤a≤25
≤a≤25
因为a为整数.
所以,到安置区建房的非安置户至少有19户且最多有25户时,政府才能将30户移民农户全部安置;否则,政府就不能将30户移民农户全部安置.
15、把x=1,y=m,代入y=6/x,得m=6.
令x=O,得y=c,所以点C的坐标是(0,c).
又OA=OC,所以点A的坐标为(-c,O).
所以(-c)2+b(-c)+c=O,又c>0,得c-b=-1.②
解①、②所组成的方程组,得b=3c=2
所以y=x2+3x+2.
16\1)略。
(2)∵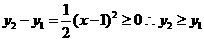
(3)联立方程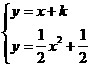 解得
解得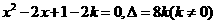
① k<0 时(2)中结论仍然成立。
② 当>0时,方程有两根: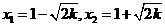 。此时抛物线上有一部分点在直线的下方,所以(2)中的结论对任意的x成立。
。此时抛物线上有一部分点在直线的下方,所以(2)中的结论对任意的x成立。
当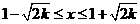 时,(2)中结论不成立。
时,(2)中结论不成立。
14、(1)设直线OM的函数关系式为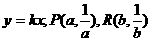 .
.
则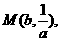 ∴
∴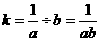 .
.
∴直线OM的函数关系式为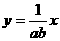 .
.
(2)∵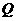 的坐标
的坐标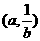 满足
满足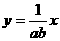 ,∴点
,∴点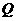 在直线OM上.
在直线OM上.
(或用几何证法,见《九年级上册》教师用书191页)
∵四边形PQRM是矩形,∴SP=SQ=SR=SM=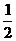 PR.
PR.
∴∠SQR=∠SRQ.
∵PR=2OP,∴PS=OP=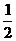 PR.∴∠POS=∠PSO. ∵∠PSQ是△SQR的一个外角,
PR.∴∠POS=∠PSO. ∵∠PSQ是△SQR的一个外角,
∴∠PSQ=2∠SQR.∴∠POS=2∠SQR.
∵QR∥OB,∴∠SOB=∠SQR. ∴∠POS=2∠SOB.
∴∠SOB=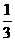 ∠AOB.
∠AOB.
(3)以下方法只要回答一种即可.
方法一:利用钝角的一半是锐角,然后利用上述结论把锐角三等分的方法即可.
13、1)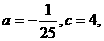 EF=10米.
EF=10米.
(3)误差估计如下:
解法一:∵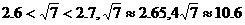 ,
,
∴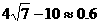 .
.
∴差的近似值约为0.6米.
解法二:∵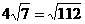 在10到11之间,可得
在10到11之间,可得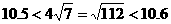 ,
,
∴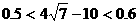 ,
,
∴差的近似值约为0.5或0.6米.
12、(1)由抛物线的顶点是M(1,4),设解析式为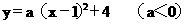
又抛物线经过点N(2,3),所以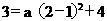 解得a=-1
解得a=-1
所以所求抛物线的解析式为y=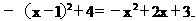
令y=0,得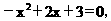 解得:
解得: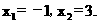
得A(-1,0) B(3,0) ;
令x=0,得y=3,所以 C(0,3).
(2)直线y=kx+t经过C、M两点,所以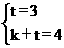 即k=1,t=3
即k=1,t=3
直线解析式为y=x+3.
令y=0,得x=-3,故D(-3,0) CD=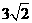
连接AN,过N做x轴的垂线,垂足为F.
设过A、N两点的直线的解析式为y=mx+n,
则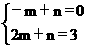 解得m=1,n=1
解得m=1,n=1
所以过A、N两点的直线的解析式为y=x+1
所以DC∥AN.
在Rt△ANF中,AN=3,NF=3,所以AN=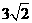
所以DC=AN。
因此四边形CDAN是平行四边形.
(3)假设在x轴上方存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,设P(1,u) 其中u>0,则PA是圆的半径且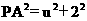
过P做直线CD的垂线,垂足为Q,则PQ=PA时以P为圆心的圆与直线CD相切。
由第(2)小题易得:△MDE为等腰直角三角形,故△PQM也是等腰直角三角形,
由P(1,u)得PE=u, PM=|4-u|, PQ=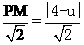
由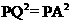 得方程:
得方程: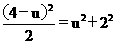 ,解得
,解得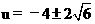 ,
,
舍去负值u=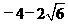 ,符合题意的u=
,符合题意的u=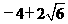 ,
,
所以,满足题意的点P存在,其坐标为(1,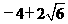 ).
).
11、⑴ ∵当Q在AB上时,显然PQ不垂直于AC。
当,由题意得:BP=x,CQ=2x,PC=4-x,
∴AB=BC=CA=4,∠C=600,
若PQ⊥AC,则有∠QPC=300,∴PC=2CQ
∴4-x=2×2x,∴x=,
∴当x=(Q在AC上)时,PQ⊥AC;
⑵ 当0<x<2时,P在BD上,Q在AC上,过点Q作QH⊥BC于H,
∵∠C=600,QC=2x,∴QH=QC×sin600=x
∵AB=AC,AD⊥BC,∴BD=CD=BC=2
∴DP=2-x,∴y=PD·QH=(2-x)·x=-
⑶ 当0<x<2时,在Rt△QHC中,QC=2x,∠C=600,
∴HC=x,∴BP=HC
∵BD=CD,∴DP=DH,
∵AD⊥BC,QH⊥BC,∴AD∥QH, ∴OP=OQ ∴S△PDO=S△DQO,
∴AD平分△PQD的面积;
⑷ 显然,不存在x的值,使得以PQ为直径的圆与AC相离
当x=或时,以PQ为直径的圆与AC相切。
当0≤x<或<x<或<x≤4时,以PQ为直径的圆与AC相交。
10、1)常数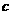 的值为
的值为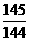 (2)正方形MNPQ的边长为
(2)正方形MNPQ的边长为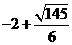
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com