17.A　　 18.B 　　19.B　　 20.C

9.B　　 10.B　　 11.B　　 12.C　　 13.B　　 14.C　　 15. D 　16.B

1.B　　 2.C　　 3.B　　 4.B　　 5.B　　 6.B　　 7.C　　 8.D

19.如图，一个中学生推铅球，铅球在点A处出手，在点B处落地，它

的运行路线是一条抛物线，在平面直角坐标系中，这条抛物线的解析式为：y=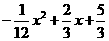

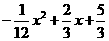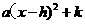(1)请用配方法把y=化成y=的形式。

(2)求出铅球在运行过程中到达最高点时离地面的距离和这个学生推铅球的成绩。(单

位：米)

20某市城建部门经过长期市场调查发现，该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P=25x；年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为Q=―10；

(1)如果年新建商品房的面积与年新房销售面积相等，求市场新房均价和年新房销售总额；

(2)在(1)的基础上，如果市场新房均价上涨1千元，那么该市年新房销售总额是增加还是减少?变化了多少?结合年新房销售总额和积压面积的变化情况，请你提出一条合理化的建议。(字数不超过50)

选择题、填空题答案

18.在黄州服装批发市场，某种品牌的时装当季节将来临时，价格呈上升趋势，设这种时装开始时定价为20元，并且每周(7天)涨价2元，从第6周开始保持30元的价格平稳销售；从第12周开始，当季节即将过去时，平均每周减价2元，直到第16周周末，该服装不再销售。

⑴ 试建立销售价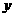与周次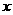之间的函数关系式；

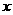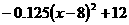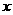⑵ 若这种时装每件进价Z与周次次之间的关系为Z＝。1≤≤16，且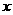为整数，试问该服装第几周出售时，每件销售利润最大？最大利润为多少？

17、.如图,五边形ABCDE为一块土地的示意图．四边形AFDE为矩

形,AE=130米，ED=100米，BC截∠F交AF、FD分别于点B、C，且BF=FC=10米．

(1)现要在此土地上划出一块矩形土地NPME作为安置区，若设PM的长为x米，矩形

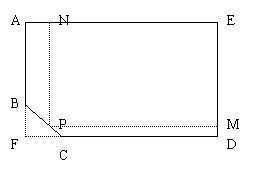NPME的面积为y平方米，求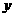与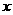的函数关系式，并求当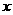为何值时，安置区的面积y最大，最大面积为多少？

(2)因三峡库区移民的需要，现要在此最大面积的安置区内安置30户移民农户，每户建

房占地100平方米，政府给予每户4万元补助，安置区内除建房外的其余部分每平方米政

府投入100元作为基础建设费，在五边形ABCDE这块土地上，除安置区外的部分每平方

米政府投入200元作为设施施工费．为减轻政府的财政压力，决定鼓励一批非安置户到此

安置区内建房，每户建房占地120平方米，但每户非安置户应向政府交纳土地使用费3万

元．为保护环境，建房总面积不得超过安置区面积的50%．若除非安置户交纳的土地使用

费外，政府另外投入资金150万元，请问能否将这30户移民农户全部安置？并说明理由．

16.已知一次函数y₁=x，二次函数y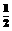₂=x²+。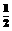

　 (1)根据表中给出的x的值，填写表中空白处的值；

x	―3	―2	―1	0	1	2	3
y1=x	―3	―2	―1	0	1	2	3
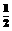y2=x2+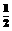			1		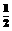1

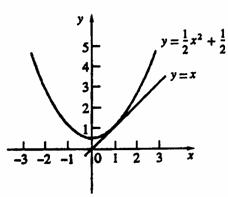　 (2)观察上述表格中的数据，对于x的同一个值，

判断y_l和y₂的大小关系。并证明：在实数范围内，对

于x的同一个值，这两个函数所对应的函数值y₁和

y₂的大小关系仍然成立；

　 (3)若把y₁=x换成与它平行的直线y=x+k(k为

任意非零实数)，请进一步探究：当k满足什么条件时，

(2)中的结论仍然成立；当k满足什么条件时，(3)

中的结论不能对任意的实数x都成立，

并确定使(2)中的结论不成立的x的范围。

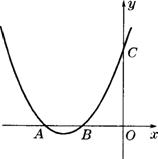
15.　 如图，抛物线y=x²+bx+c与x轴的负半轴相交于A、B两点，与y轴的正半轴相交于C点，与双曲线y=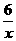的一个交点是(1，m)，且OA=OC.求抛物线的解析式．

14. “三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图)：将给定的锐角∠AOB置于直角坐标系中，边OB在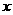轴上、边OA与函数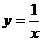的图象交于点P，以P为圆心、以2OP为半径作弧交图象于点R．分别过点P和R作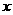轴和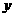轴的平行线，两直线相交于点M ，连接OM得到∠MOB，则∠MOB=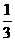∠AOB．要明白帕普斯的方法，请研究以下问题：

(1)设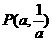、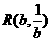，求直线OM对应的函数表达式(用含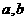的代数式表示)．

(2)分别过点P和R作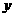轴和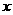轴的平行线，两直线相交于点Q．请说明Q点在直线OM上，并据此证明∠M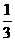OB=∠AOB．

(3)应用上述方法得到的结论，你如何三等分一个钝角(用文字简要说明)．

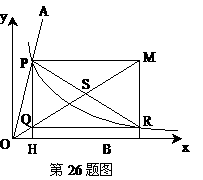
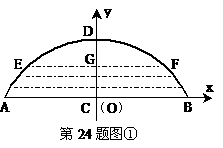
13.一座拱型桥，桥下水面宽度AB是20米，拱高CD是4米．若水面上升3米至EF，则水面宽度EF是多少？

(1)若把它看作是抛物线的一部分，在坐标系中(如图①)可设抛物线的表达式为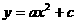．请你填空：

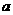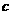=　　　　　　 ，=　　　　　　 ，EF =　　　　　　 米．

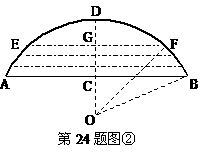
(2)若把它看作是圆的一部分，则可构造图形(如图②)计算如下：

设圆的半径是米，在Rt△OCB中，易知

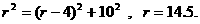
同理，当水面上升3米至EF，在Rt△OGF中可计算出GF=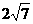，即水面宽度EF=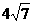米．

(3)请估计(2)中EF与(1)中你计算出的EF的差的近似值(误差小于0.1米)．