5.若ΔABC中,锐角A满足­丨sinA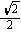－­­丨+cos²C=0.则ΔABC是(　 )。

­A．等腰直角三角形　　　　　　 　B．等腰三角形

C．直角三角形　　　　　　　　　 D．锐角三角形

4.在RtΔABC中,∠C=90⁰,则下列等式中不正确的是(　 )。

A．a=csinA　　 B．­a=bcotB　　　 C．­b=csinB　　 D．c=­­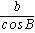

3.若sin²40⁰+sin²α=1,且α为锐角,则α等于(　 )。

A．30⁰ B．40⁰ C．­50⁰ D．­60⁰

2.若A为锐角,且sinA=­­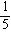,则角A满足(　 )。

A．0⁰<A<30⁰ B．­30⁰<A<45⁰ C．­45⁰<A<60⁰ D．­60⁰<A<90⁰

1.当锐角A<60⁰时,下列结论不正确的是(　 )。

A．sinA<­­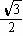 　B．cosA<­­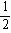　　 ­C．tanA<­­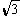　　 ­D．cotA>­­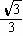

7．已知抛物线y=ax²(a>0)上有两点A、B，其横坐标分别为－1，2，请探求关于a的取值情况，△ABO可能是直角三角形吗？不能，说明理由；能是直角三角形，写出探求过程。

6.如图，直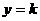线和双曲线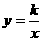相交于点P，过P点作PA₀垂直x轴，垂足A₀，x轴上的点A₀、A₁、A₂、……、A_n的横坐标是连续整数。过点A₁、A₂、……、A_n分别作x轴的垂线，与双曲线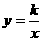(x > 0)及直线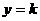分别交于点B₁、B₂、……、B_n、C₁、C₂、……、C_n.

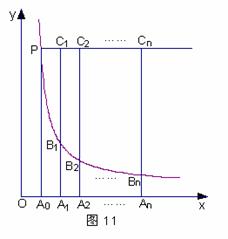⑴求A₀点坐标；

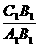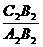⑵求及的值；

⑶试猜想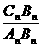的值(直接写答案)

5.施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM

为12米.现以O点为原点，OM所在直线为X轴建立直角坐标系(如图所

示)。

(1)直接写出点M及抛物线顶点P的坐标；

(2)求出这条抛物线的函数解析式；

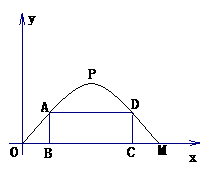(3)施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下.

4.如图，二次函数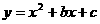的图象经过点M(1，-2)、N(-1，6)。

(1)求二次函数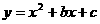的关系式。(3分)

(2)把Rt△ABC放在坐标系内，其中∠CAB = 90°，点A、B的坐标分别为(1，0)、(4，0)，BC = 5。将△ABC沿x轴向右平移，当点C落在抛物线上时，求△ABC平移的距离。(4分)

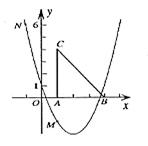
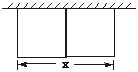
3.如图，要建一个长方形养鸡场，鸡场的一边靠墙，如果用50 m长的篱笆围成中间有一道篱笆隔墙的养鸡场，设它的长度为x m.

(1)要使鸡场面积最大，鸡场的长度应为多少m？

(2)如果中间有n(n是大于1的整数)道篱笆隔墙，要使鸡场面积最大，

鸡场的长应为多少m？比较(1)(2)的结果，你能得到什么结论？