
题目列表(包括答案和解析)
9、∵函数y=x2+b++c图象过点(0,-3)得c=-3
∴函数解析式为y=x2+bx-3
又∵该二次函数图象与x轴相交于A(x1,0),B(x2,0)两点,所以方程y=x2+bx-3
两个根分别为x1,x2
则有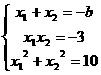 解得b=
解得b=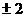
∴二次函数为y=x2+2x-3或y=x2-2x-3'
8、⑴ C(1,1),D(2,4)
OC: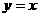 ,M(2,2)
,M(2,2)
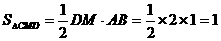
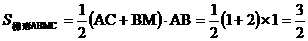
∴
又CD: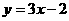 ,H(0,
,H(0,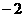 )
)
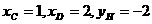 ∴
∴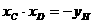
⑵ 结论①仍成立
∵A(t,0),B(2t,0),C(t,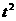 ),D
),D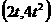 OC:
OC: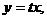 M
M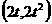
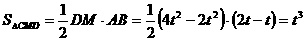
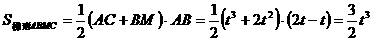
∴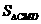 :
: =2 :3
=2 :3
⑶ C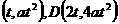 CD:
CD: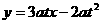 H
H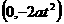
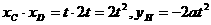
∴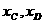 和
和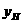 的数值关系为:
的数值关系为: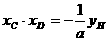
7、1)菱形:AHBG,EBFC,AFDE
等腰梯形:HGEF,BCMH,AHMD
梯形:DMHC,MHAB
平行四边形:EGFM,AHMC,MHBD,AGDM
(2)在四边形EBFC中,
∵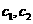 关于y轴对称 ∴OC=OB
关于y轴对称 ∴OC=OB
∵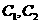 关于x轴对称 ∴OE=OF 又EF⊥OB
关于x轴对称 ∴OE=OF 又EF⊥OB
∴EBFC为菱形
(3)菱形的性质有:①四条边相等 ②对角线互相垂直平分 ③每一条对角线平分一组对角 ④对角相等
6、(1)40-25=15故矩形的宽为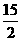 ∴
∴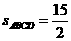 ×25=187.5
×25=187.5
(2)设利用 的墙作为矩形羊圈的长,则宽为
的墙作为矩形羊圈的长,则宽为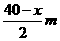 ,设矩形的面积为
,设矩形的面积为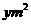 ,
,
则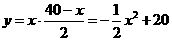
∵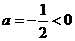 ,故当
,故当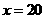 时,
时,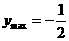
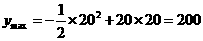
∵200>187.5故张大伯设计不合理,应设计为长20m,宽10m利用20m墙的矩形羊圈
4、(1) 由已知:OC=0.6,AC=0.6, 得点A的坐标为(0.6,0.6),
代入y=ax2,得a=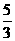 , ∴抛物线的解析式为y=
, ∴抛物线的解析式为y=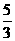 x2.
x2.
(2)点D1,D2的横坐标分别为0.2,0.4,
代入y=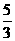 x2,得点D1,D2的纵坐标分别为:y1=
x2,得点D1,D2的纵坐标分别为:y1=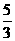 ×0.22≈0.07,y2=
×0.22≈0.07,y2=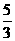 ×0.42≈0.27,
×0.42≈0.27,
∴立柱C1D1=0.6-0.07=0.53,C2D2=0.6-0.27=0.33,
由于抛物线关于y轴对称,栅栏所需立柱的总长度为:
2(C1D1+ C2D2)+OC=2(0.53+0.33)+0.6≈2.3米.
5\(1)
由已知,矩形的另一边长为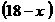

则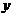 =
= 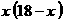 =
=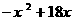
自变量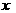 的取值范围是0<
的取值范围是0<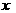 <18.
<18.
(2)∵ 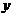 =
=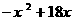 =
=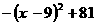
∴ 当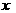 =9时(0<9<18),苗圃的面积最大
=9时(0<9<18),苗圃的面积最大
最大面积是81 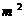
又解: ∵  =-1<0,
=-1<0,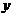 有最大值,
有最大值,
∴
当 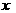 =
=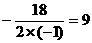 时(0<9<18),
时(0<9<18),
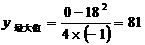 (
(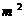 )
)
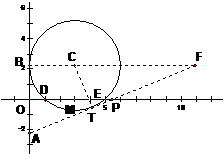
3、解:(1)连BC,则BC⊥y轴。
取DE中点M,连CM,则CM⊥x轴。
∵OD=1,OE=5,∴OM=3。
∵OB2=OD·OE=5,∴OB=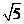 。
。
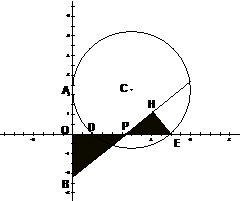 ∴圆心C
∴圆心C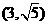 ,半径R=3。
,半径R=3。
(2)∵△POA≌△PHE,∴PA=PE。
∵OA=OB=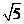 ,OE=5,OP=a,∴
,OE=5,OP=a,∴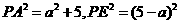 ,
,
∴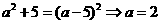
(3)解法一:
过点A作⊙C的切线AT(T为切点)交x正半轴于Q,设Q(m,0),则QE=m-5,QD=m-1,
QT=QA-AT=QA-AB=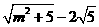
由OT2=OE·OD,得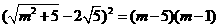
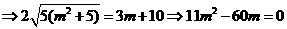
 ∵
∵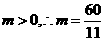 ∵a=6,点P(6,0)在点Q
∵a=6,点P(6,0)在点Q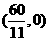 的右侧,
的右侧,
∴直线AP与⊙C相离。
解法二:
设射线AP、BC交于点F,作CT⊥AF于T,则
∵△AOP∽△CTF,∴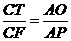
而AO=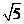 ,AP=
,AP=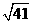 ,CF=BF-BC=12-3=9,
,CF=BF-BC=12-3=9,
∴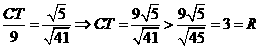 ,
,
∴直线AP与⊙C相离
2、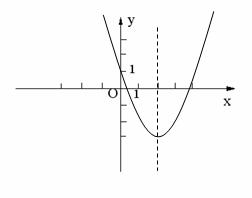 (1)∵
(1)∵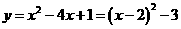 ,
,
∴当x=2时,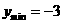 .
.
(2)如图,图象是一条开口向上的抛物线。
对称轴为x=2,顶点为(2,-3)。
(3)由题意,x1,x2,是方程x2-4x+1=0的两根,
∴x1+x2=4,x1x2=1.
∴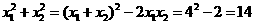
1、(1) 在Rt△OAB中,∵∠AOB=30°,∴ OB=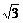 . 过点B作BD垂直于x轴,垂足为D,则 OD=
. 过点B作BD垂直于x轴,垂足为D,则 OD=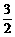 ,BD=
,BD=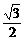 ,∴ 点B的坐标为(
,∴ 点B的坐标为(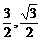 ) .
) .
(2) 将A(2,0)、B(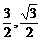 )、O(0,0)三点的坐标代入y=ax2+bx+c,得
)、O(0,0)三点的坐标代入y=ax2+bx+c,得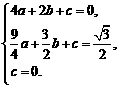
解方程组,有 a=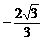 ,b=
,b=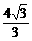 ,c=0.
,c=0.
∴ 所求二次函数解析式是 y=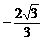 x2+
x2+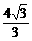 x.
x.
(3) 设存在点C(x , 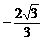 x2+
x2+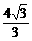 x) (其中0<x<
x) (其中0<x<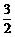 ),使四边形ABCO面积最大.
),使四边形ABCO面积最大.
∵△OAB面积为定值,
∴只要△OBC面积最大,四边形ABCO面积就最大.
过点C作x轴的垂线CE,垂足为E,交OB于点F,则
S△OBC= S△OCF +S△BCF=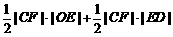 =
=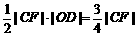 ,
,
而 |CF|=yC-yF=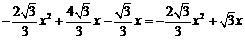 ,
,
∴ S△OBC=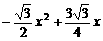 .
.
∴ 当x=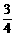 时,△OBC面积最大,最大面积为
时,△OBC面积最大,最大面积为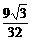 .
.
此时,点C坐标为(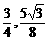 ),四边形ABCO的面积为
),四边形ABCO的面积为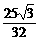 .
.
4. 略
5.x<2
x>2
x=2 6. 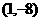 7.1,3=
7.1,3=
1.略(答案不惟一) y=(x-2)2+3等 2.
(1,-8)
3.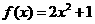
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com