
题目列表(包括答案和解析)
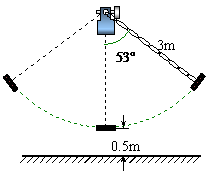
5.如图所示,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为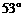 ,则秋千踏板与地面的最大距离约为多少?(参考数据:
,则秋千踏板与地面的最大距离约为多少?(参考数据: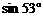 ≈0.8,
≈0.8,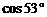 ≈0.6)
≈0.6)
4.大楼AD的高为10米,远处有一塔BC,某人在楼底A处测得踏顶B处的仰角为60º,爬到楼顶D点测得塔顶B点的仰角为30º,求塔BC的高度。
3.如图5,某校自行车棚的人字架棚顶为等腰三角形,
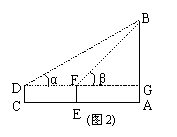
 D是AB的中点,中柱CD=1米,∠A=27°,
D是AB的中点,中柱CD=1米,∠A=27°,
求跨度AB的长(精确到0.01米)。

2.(A类)如图1,在与旗杆AB相距20米的C处,用高1.20米的测角仪测得旗杆顶端B的仰角α=30°.求旗杆AB的高(精确到0.1米).
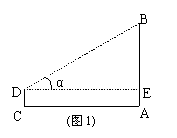 (B类)如图9,在C处用高1.20米的测角仪测得塔AB顶端B的仰角α=30º,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).
(B类)如图9,在C处用高1.20米的测角仪测得塔AB顶端B的仰角α=30º,向塔的方向前进20米到E处,又测得塔顶端B的仰角β=45°.求塔AB的高(精确到0.1米).
我选做______________类题,解答如下:
1.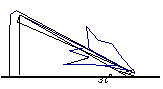 如图,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30º夹角,这棵大树在折断前的高度为
如图,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30º夹角,这棵大树在折断前的高度为
A.10米 B.15米
C.25米 D.30米
3.我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分。(如下图1)
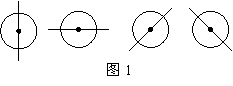
探索下列问题:
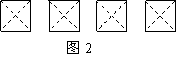
(1)在图2给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线),将每个正方形都分割成面积相等的两部分;
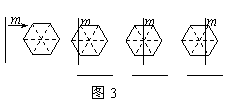
(2)一条竖直方向的直线m以及任意的直线n,在由左向右平移的过程中,将正六边形分成左右两部分,其面积分别记为S1和S2.
①请你在图3中相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接);
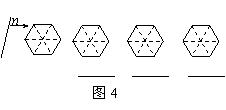 ②请你在图4中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接).
②请你在图4中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接).
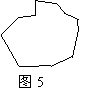
(3)是否存在一条直线,将一个任意的平面图 形(如图5)分割成面积相等的两部分,请简略说出理由.
4右图为人民公园中的荷花池,现要测量此荷花池两旁A、B两棵树间的距离(我们不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案.
要求:(1)画出你设计的测量平面图;
(2)简述测量方法,并写出测量的数据(长度用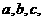 …表示;角度用
…表示;角度用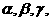 …表示);
…表示);
(3)根据你测量的数据,计算A、B两棵树间的距离.
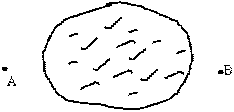
①.一位园艺设计师计划在一块形状为直角三角形 且有一个内角为60o的绿化带上种植四种不同的花卉,要求种植的四种花卉分别组成面积相等,形状完全相同的几何图形图案.某同学为此提供了如图所示的五种设计方案.其中可以满足园艺设计师要求的有( )
(A) 2种 (B) 3种 (C) 4种 (D) 5种
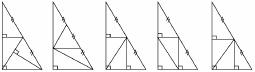
②.如图1,A、B两点被池塘隔开,为测量AB两点的距离,在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN=20m,那么AB=2×20m=40m。
(1)测AB距离也可由图2所示用三角形相似知识来解决,请根据题意填空:延长AC到D,使CD=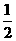 AC,延长BC到E,使CE=________,则由相似三角形得,AB=_______.
AC,延长BC到E,使CE=________,则由相似三角形得,AB=_______.
(2)测AB距离还可由三角形全等的知识来设计测量方案,求出AB的长,请用上面类似的方法,在图3中画出图形,并叙述你的测量方案。

 ③.李大爷有一个边长为a的正方形鱼塘,如图,鱼塘四个角的顶点A、B、C、D上各有一棵大树。现在李大爷想把原来的鱼塘扩建成一个圆形或正方形鱼塘(原鱼塘周围的面积足够大),又不想把树挖掉(即四棵大树要在新建鱼塘的边沿上)。
③.李大爷有一个边长为a的正方形鱼塘,如图,鱼塘四个角的顶点A、B、C、D上各有一棵大树。现在李大爷想把原来的鱼塘扩建成一个圆形或正方形鱼塘(原鱼塘周围的面积足够大),又不想把树挖掉(即四棵大树要在新建鱼塘的边沿上)。
(1)若按圆形设计,画出你所设计的圆形鱼塘示意图,并求出圆形鱼塘的面积;
(2)若按正方形设计,画出你所设计的正方形鱼塘示意图;
(3)你在(2)所设计的正方形鱼塘中,有无最大面积?为什么?
(4)李大爷想使新建鱼塘面积最大,你认为新建鱼塘的最大面积是多少?
2.在湖的两岸A、B间建一座观赏桥,由于条件限制,无法直接度量A、B两点间的距离。请你用学过的数学知识按以下要求设计一测量方案。
(1)画出测量图案;
(2)写出测量步骤(测量数据用字母表示);
(3)计算AB的距离(写出求解或推理过程,结果用字母表示)。

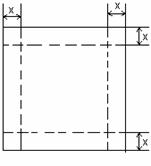
1.如图,一张边长为16㎝的正方形硬纸板,把它的四个角都剪去一个边长为x㎝的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为V㎝3,
请回答下列问题:
(1)若用含有X的代数式表示V,则V=
(2)完成下表:
|
x(㎝) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
V(㎝3) |
196 |
288 |
|
|
180 |
96 |
28 |
(3) 观察上表,容积V的值是否随x值得增大而增大?当x取什么值时,容积V的值最大?
解:
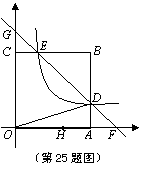
25. 如图,边长为a的正方形OABC与双曲线在第一象限的图象交于D、E两点,S△OAD=;过D、E两点的直线分别交坐标轴于点F、G,过F、G两点的抛物线y=x2+mx+n与x轴相交于另一点H.
⑴求双曲线的解析式;
⑵是否存在这样的a值,使直线AB为抛物线y=x2+mx+n的对称轴?若存在,求出a的
值;若不存在,说明理由;
⑶若OH:HF=2:3,求抛物线y=x2+mx+n的顶点坐标.
24.BS超市常年为HY厂代销J型家用微波炉,其销售方式是直接从HY厂按出厂价进货,然后适当加价销售.超市以每台700元的价格销售J型微波炉,可获得40%的利润.2007年元旦来临,厂家和超市为扩大销量、增加利润,决定在元旦假期联合进行降价、让利促销活动.超市对过去J型微波炉的市场销售情况进行了调查:若按原价销售,平均每天可销售10台;若每台降价20元,平均每天可多销4台.厂家对超市承诺:在元旦促销期间销售的J型微波炉的批发价每台优惠20元;对多销的部分,厂家每台再让利50元.
(1)2007年元旦前,BS超市销售一台J型微波炉可获利多少元?
(2)经统计,仅元旦假期三天中,通过降价销售及厂家让利,BS超市销售J型微波炉共获得利润13800元,HY厂也从中获得了丰厚的利润,平均每天的销售收入比BS超市获得的总利润还要多.请你计算元旦期间SB超市确定的J型微波炉的销售单价.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com