
题目列表(包括答案和解析)
22.解:(1) 四边形
四边形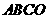 是正方形,∴BC=OA=OC=4,
是正方形,∴BC=OA=OC=4, 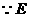 为
为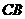 中点,
中点,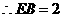
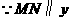 轴,
轴,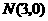 ,
,
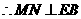 且
且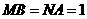
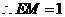 …………………(1分)而
…………………(1分)而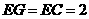 ,
,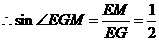
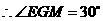 ………………………………………(2分)
………………………………………(2分)
 (2)
(2)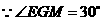
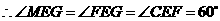

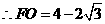
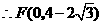 ,
,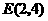
设直线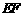 的解析式为
的解析式为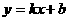 ,则
,则
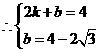
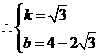
 折痕
折痕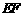 所在直线解析式为
所在直线解析式为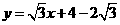 ·········································································· (5分)
·········································································· (5分)
(3)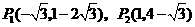 ,
,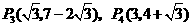 .。。。。。。。。(9分)
.。。。。。。。。(9分)
本资料由《七彩教育网》 提供!
21. (1)解:CD与AC互相垂直。 …………(1分)
证明:连结OD,∵OB=OD,∴∠ODB=∠B,
 ∵AC=BC,∴∠A=∠B,∴∠A=∠ODB,
∵AC=BC,∴∠A=∠B,∴∠A=∠ODB,
∴OD∥AC,∵⊙O与直线CD相切,∴CD⊥OD,
∴CD⊥AC……………………………(4分)
(2)解:∵ ΔACB∽ΔCDB且AC=BC,
∴CD=DB ,∴∠A=∠B=∠DCB,
又∵∠A+∠B+∠DCB+∠ACD=180°,∠ACD=90°,
∴∠A=∠B=∠DCB=30°,…………………………(6分)
在RtΔACD和RtΔCDO中,OD=CD·tan∠DCB, CD=AC·tan∠A,∴OB=OD=
AC·tan∠A·tan∠DCB=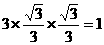 …………………(8分)过点O作OE⊥AB于E,则OE=
…………………(8分)过点O作OE⊥AB于E,则OE=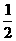 OB=
OB=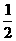 ,即圆心O到直线AB的距离为
,即圆心O到直线AB的距离为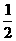 。(9分)
。(9分)
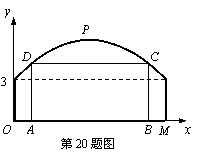
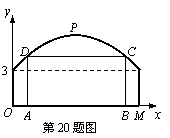
20.(1) M(12,0),P(6,6). ………………………………………………………………………………………2分
 (2) 设此函数关系式为:
(2) 设此函数关系式为: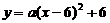 . ………………………………………………………3分
. ………………………………………………………3分
∵函数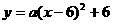 经过点(0,3),
经过点(0,3),
∴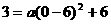 ,即
,即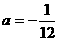 . ………………4分
. ………………4分
∴此函数解析式为:
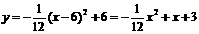 .………5分
.………5分
(3) 设A(m,0),则
B(12-m,0),C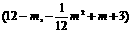 ,D
,D 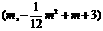 . …………7分
. …………7分
∴“支撑架”总长AD+DC+CB = 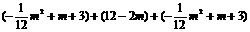 =
=
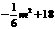 . ∵ 此二次函数的图象开口向下.∴ 当m = 0时,AD+DC+CB有最大值为18. …………………………………………………9分
. ∵ 此二次函数的图象开口向下.∴ 当m = 0时,AD+DC+CB有最大值为18. …………………………………………………9分
19.解:(1)设打包成件的帐篷有x件,则 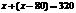 (或
(或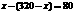 )
…………2分
)
…………2分
解得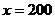 ,
,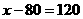 …………………………3分答:打包成件的帐篷和食品分别为200件和120件. …………………………3分方法二:设打包成件的帐篷有x件,食品有y件,则
…………………………3分答:打包成件的帐篷和食品分别为200件和120件. …………………………3分方法二:设打包成件的帐篷有x件,食品有y件,则
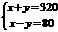 ……………2分解得
……………2分解得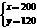 ……………3分
……………3分
答:打包成件的帐篷和食品分别为200件和120件. ……………3分(注:用算术方法做也给满分.)
(2)设租用甲种货车x辆,则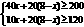 …5分解得
…5分解得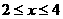 ……6分∴x=2或3或4,民政局安排甲、乙两种货车时有3种方案.设计方案分别为:①甲车2辆,乙车6辆;②甲车3辆,乙车5辆;③甲车4辆,乙车4辆.
……………………7分
……6分∴x=2或3或4,民政局安排甲、乙两种货车时有3种方案.设计方案分别为:①甲车2辆,乙车6辆;②甲车3辆,乙车5辆;③甲车4辆,乙车4辆.
……………………7分
13 证三角形全等即可14、(1)不合格 (2)80名 (3)合理,理由,利用样本的优秀人数来诂计总体的优秀人数。
15.解:(1)把A(-2,1)代入y=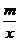 ,得m=-2,即反比例函数为y=-
,得m=-2,即反比例函数为y=-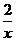 ,则n=
,则n=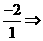 n=-2. 即B(1,-2),把A(-2,1),B(1,-2)代入y=kx+b, 求得k=-1,b=-1,所以y=-x-1. (2)x<-2或0<x<1.16.解:在
n=-2. 即B(1,-2),把A(-2,1),B(1,-2)代入y=kx+b, 求得k=-1,b=-1,所以y=-x-1. (2)x<-2或0<x<1.16.解:在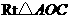 中,
中,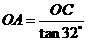 1分在
1分在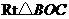 中,
中,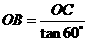 .2分
.2分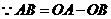 ,
,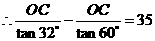 ,3分
,3分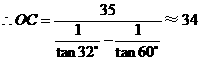 (米) 5分答:三元塔的高度约是34米. 7分17(1)
(米) 5分答:三元塔的高度约是34米. 7分17(1)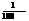 ,
,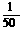 ,
,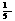 (2)解:依题意得:
(2)解:依题意得: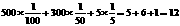 (元)
(元) 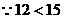 ∴应选择第二种18. 解:⑴设所围矩形ABCD的长AB为x米,则宽AD为
∴应选择第二种18. 解:⑴设所围矩形ABCD的长AB为x米,则宽AD为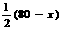 米. 依题意,得
米. 依题意,得 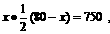
即,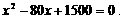 解此方程,得
解此方程,得 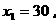
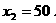 ∵墙的长度不超过45m,∴
∵墙的长度不超过45m,∴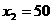 不合题意,应舍去. 当
不合题意,应舍去. 当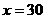 时,
时,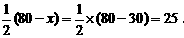 所以,当所围矩形的长为30m、宽为25m时,能使矩形的面积为750m2.
所以,当所围矩形的长为30m、宽为25m时,能使矩形的面积为750m2.
⑵不能.因为由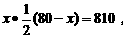 得
得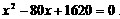 又∵
又∵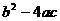 =(-80)2-4×1×1620=-80<0,
=(-80)2-4×1×1620=-80<0,
∴上述方程没有实数根.因此,不能使所围矩形场地的面积为810m2
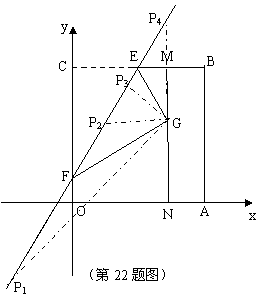
22.如图,四边形 是一张放在平面直角坐标系中的正方形纸片.点
是一张放在平面直角坐标系中的正方形纸片.点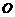 与坐标原点重合,点
与坐标原点重合,点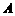 在
在 轴上,点
轴上,点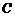 在
在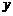 轴上,
轴上,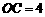 ,点
,点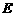 为
为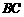 的中点,点
的中点,点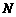 的坐标为
的坐标为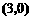 ,过点
,过点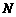 且平行于
且平行于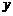 轴的直线
轴的直线 与
与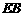 交于点
交于点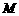 .现将纸片折叠,使顶点
.现将纸片折叠,使顶点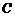 落在
落在 上,并与
上,并与 上的点
上的点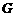 重合,折痕为
重合,折痕为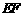 ,点
,点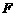 为折痕与
为折痕与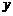 轴的交点.
轴的交点.
(1)求∠EGM的度数;
(2)求折痕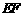 所在直线的解析式;
所在直线的解析式;
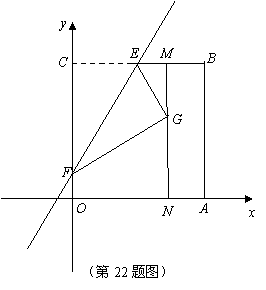 (3)设点
(3)设点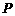 为直线
为直线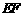 上的点,是否存在这样的点
上的点,是否存在这样的点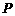 ,使得以
,使得以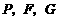 为顶点的三角形为等腰三角形,若存在,请直接写出点
为顶点的三角形为等腰三角形,若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
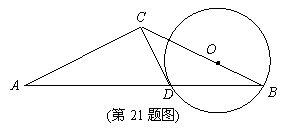
21.如图,ΔABC中,AC=BC,以BC上一点O为圆心、OB为半径作⊙O交AB于点D。已知经过点D的⊙O切线恰好经过点C。
(1)试判断CD与AC的位置关系,并证明。
(2)若ΔACB∽ΔCDB,且AC=3,求圆心O到直线AB的距离。
20. 如图,某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.(1) 直接写出点M及抛物线顶点P的坐标;(2) 求出这条抛物线的函数解析式;(3) 若要搭建一个矩形“支撑架”AD+DC+CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
19、“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.(1)求打包成件的帐篷和食品各多少件?(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
18、如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
⑴怎样围才能使矩形场地的面积为750m2?
⑵能否使所围矩形场地的面积为810m2,为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com