
题目列表(包括答案和解析)
4.不等式组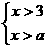 的解集是x>
的解集是x>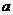 ,则
,则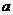 的取值范围是( )。
的取值范围是( )。
A.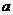 ≥3 B.
≥3 B.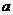 =3
C.
=3
C.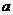 >3
D.
>3
D.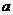 <3
<3
3. 已知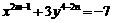 是关于x、y的二元一次方程,则m、n的解是( )。
是关于x、y的二元一次方程,则m、n的解是( )。
A.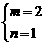 B.
B. 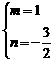 C.
C.
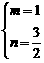 D.
D.
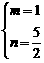
2.点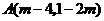 在第三象限,那么
在第三象限,那么 值是( )。
值是( )。
A.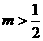 B.
B.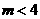 C.
C.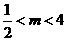 D.
D.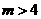
1.方程 2 x2 + x = 0 的解为( )。
A.x1 = 0 x 2= B. x1 = 0 x 2=-2
C. x = - D. x1 = 0 x 2 =-
7.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克.针对这种水产品的销售情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式(不必写出x的取值范围);
(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
6.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间满足函数关系:y=-0.1x2+2.6x+43(0<x<30)。y值越大,表示接受能力越强。
(1)x在什么范围内,学生的接受能力逐步增强?x在什么范围内,学生的接受能力逐步降低?
(2)第10分时,学生的接受能力是什么?
(3)第几分时,学生的接受能力最强?
(4)结合本题针对自己的学习情况有何感受?
5.已知二次函数y=(m2-2)x2-4mx+n的图象的对称轴是x=2,且最高点在直线y=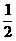 x+1上,求这个二次函数的表达式.
x+1上,求这个二次函数的表达式.
4.如图,抛物线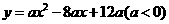 与
与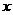 轴交于
轴交于 、
、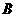 两点(点
两点(点 在点
在点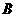 的左侧),抛物线上另有一点
的左侧),抛物线上另有一点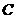 在第一象限,满足∠
在第一象限,满足∠ 为直角,且恰使△
为直角,且恰使△ ∽△
∽△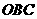 。
。
(1)求线段 的长。
的长。
(2)求该抛物线的函数关系式。
 (3)在
(3)在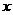 轴上是否存在点
轴上是否存在点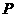 ,使△
,使△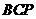 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的 点的坐标;若不存在,请说明理由。
点的坐标;若不存在,请说明理由。
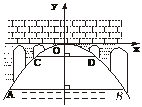
3.有一座抛物线形拱桥,桥下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米;
(1)在如图的坐标系中,求抛物线的表达式。
(2)若洪水到来时,再持续多少小时才能到拱桥顶?(水位以每小时0.2米的速度上升)
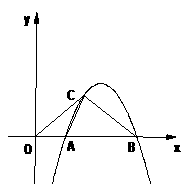
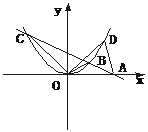
2.如图,直线AB过x轴上的点A(2,0),且与抛物线y=ax2相交于B、C两
点,B点坐标为(1,1)。
(1)求直线和抛物线所表示的函数表达式;
(2)在抛物线上是否存在一点D,使得S△OAD=S△OBC,若不存在,说明理由;若存在,请求出点D的坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com