
题目列表(包括答案和解析)
1.计算-1-1的结果是( )
A.0 B.1 C.2 D.-2
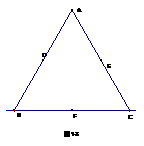
25. 已知等边三角形ABC中,点D、E、F分别为AB、AC、BC边的中点,M为直线BC上一动点,
已知等边三角形ABC中,点D、E、F分别为AB、AC、BC边的中点,M为直线BC上一动点, 为等边三角形(点M的位置改变时,
为等边三角形(点M的位置改变时, 也随之整体移动).
也随之整体移动).
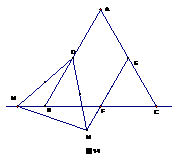
(1) 如图1-1,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?请直接写出结论,
不必证明或说明理由;
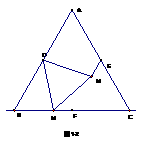
(2) 如图1-2,当点M在BC边上,其它条件不变时,(1)的结论中EN与MF的数量关系是否依然
成立?若成立,请利用图1-2证明;若不成立,请说明理由;
(3) 若点M在点C右侧时,请你在图1-3中作出相应的图形(不写作法),(1)结论中EN与MF的数
量关系是否仍然成立?请直接写出结论,不必证明或说明理由.
24.已知抛物线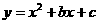 经过点A(0,5)和B(3,2)点.
经过点A(0,5)和B(3,2)点.
(1)求抛物线的解析式;
(2)现有一半径为1,圆心P在抛物线上运动的动圆,问当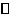 P在运动过程中,是否存在
P在运动过程中,是否存在 P与坐标轴相切的情况?若存在,请求出圆心P的坐标;若不存在,请说明理由;
P与坐标轴相切的情况?若存在,请求出圆心P的坐标;若不存在,请说明理由;
(3)若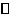 Q的半径为r,点Q在抛物线上,当
Q的半径为r,点Q在抛物线上,当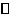 Q与两坐标轴都相切时,求半径r的值.
Q与两坐标轴都相切时,求半径r的值.
.
23. 关于x的方程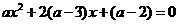 至少有一个整数解,且a是整数,求a的值.
至少有一个整数解,且a是整数,求a的值.
22. (本小题满分5分)
(本小题满分5分)
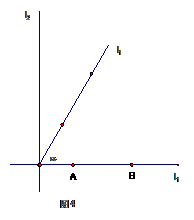
如图4所示,直线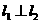 ,垂足为点
,垂足为点 ,A、B是直线
,A、B是直线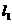
上的两点,且OB=2,AB=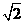 ,直线
,直线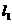 绕点O按逆时针
绕点O按逆时针
方向旋转,旋转角度为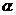
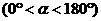 。
。
(1)
当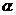 =60
=60 时,在直线
时,在直线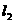 上找点P,使得
上找点P,使得 BPA是以
BPA是以
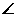 B为顶角的等腰三角形,此时OP= ;
B为顶角的等腰三角形,此时OP= ;
(2)
当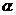 在什么范围内变化时,直线
在什么范围内变化时,直线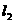 上存在点P,使得
上存在点P,使得
|
 BPA是以
BPA是以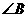 为顶角的等腰三角形,请用不等式表
为顶角的等腰三角形,请用不等式表
示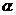 的取值范围:
.
的取值范围:
.
21.(本小题满分5分)
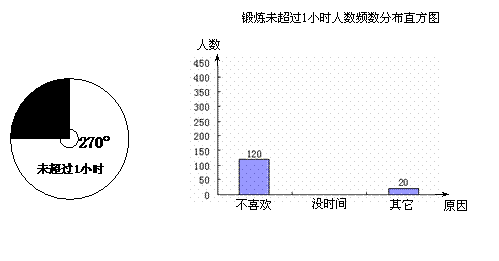
国家教委规定“中小学生每天在校体育活动时间不低于1小时”.为此,某地区今年初中毕业生学业考试体育学科分值提高到40分,成绩记入考试总分.某中学为了了解学生体育活动情况,随机调查了720名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,所得的数据制成了的扇形统计图和频数分布直方图.
根据图示,解答下列问题:
(1)若在被调查的学生中随机选出一名学生测试其体育成绩,选出的恰好是“每天锻炼 超过1小时”的学生的概率是多少?
(2)“没时间”的人数是多少?并补全频数分布直方图;
(3)2008年这个地区初中毕业生约为4.3万人,按此调查,可以估计2008年这个地区初中毕业生中每天锻炼未超过1小时的学生约有多少万人?
 (4)请根据以上结论谈谈你的看法.
(4)请根据以上结论谈谈你的看法.
解:
20.(本小题满分5分)
北京市在城市建设中,要折除旧烟囱 (如图所示),在烟囱正西方向的楼
(如图所示),在烟囱正西方向的楼 的顶端
的顶端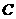 ,测得烟囱的顶端
,测得烟囱的顶端 的仰角为
的仰角为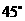 ,底端
,底端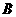 的俯角为
的俯角为 ,已量得
,已量得
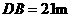 . 拆除时若让烟囱向正东倒下,试问:距离烟囱东方
. 拆除时若让烟囱向正东倒下,试问:距离烟囱东方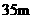 远的一棵大树是否被歪倒的烟囱砸着?请说明理由.(
远的一棵大树是否被歪倒的烟囱砸着?请说明理由.(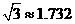 )
)
 解:
解:
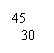

19. (本小题满分5分)
(本小题满分5分)
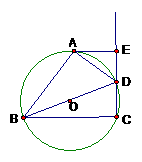 如图,四边形ABCD内接于
如图,四边形ABCD内接于 ,BD是
,BD是 的直径,
的直径,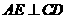 于E,
于E,
DA平分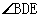 .
.
(1)求证:AE是 的切线;
的切线;
(2)若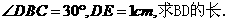
(1) 证明:

(2) 解:
18.(本小题满分5分)
在平面直角坐标xoy系中,直线y= -x关于y轴的对称直线l与反比例函数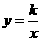 的图象的一个交点为A(a,3),试确定反比例函数的解析式.
的图象的一个交点为A(a,3),试确定反比例函数的解析式.
解:
17. (本小题满分5分)
(本小题满分5分)
某服装厂准备加工300套演出服.在加工60套后,采用了新技术,使每天的工作
效率是原来的2倍,结果共用9天完成任务.求该厂原来每天加工多少套演出服.
解:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com