
题目列表(包括答案和解析)
27.(本小题满分12分)
定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
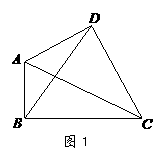
⑴如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段 .
⑵在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由. 友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.(改编)
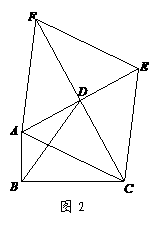
⑶如图2,,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由. 若此时AB=3,BD=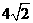 ,求BC的长. (自编)
,求BC的长. (自编)
26.(本小题满分10分)
已知抛物线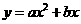 (a≠0)的顶点在直线
(a≠0)的顶点在直线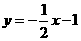 上,且过点A(4,0).
上,且过点A(4,0).
⑴求这个抛物线的解析式;
⑵设抛物线的顶点为P,是否在抛物线上存在一点B,使四边形OPAB为梯形?若存在,求出点B的坐标;若不存在,请说明理由.
⑶设点C(1,-3),请在抛物线的对称轴确定一点D,使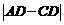 的值最大,请直接写出点D的坐标. (自编)
的值最大,请直接写出点D的坐标. (自编)
25. (本小题满分10分)
如图①,一条笔直的公路上有A、B、C 三地,B、C 两地相距 150 千米,甲、乙两辆汽车分别从B、C 两地同时出发,沿公路匀速相向而行,分别驶往C、B 两地.甲、乙两车到A 地的距离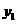 、
、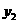 (千米)与行驶时间 x(时)的关系如图②所示.
(千米)与行驶时间 x(时)的关系如图②所示.
根据图象进行以下探究:
⑴请在图①中标出 A地的位置,并作简要的文字说明;
⑵求图②中M点的坐标,并解释该点的实际意义.
⑶在图②中补全甲车的函数图象,求甲车到 A地的距离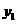 与行驶时间x的函数关系式.
与行驶时间x的函数关系式.
⑷A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.(根据南京2008中考题改编)
23.(本小题满分10分)
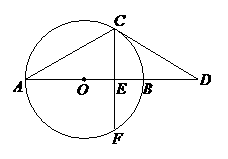
如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
⑴求∠A的度数;
⑵若点F在⊙O上,CF⊥AB,垂足为E,CF=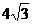 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
(自编)
22.(本小题满分8分)
为切实减轻中小学生课业负担、全面实施素质教育,某中学对本校学生课业负担情况进行调查. 在本校随机抽取若干名学生进行问卷调查,发现被抽查的学生中,每天完成课外作业时间,最长不足120分钟,没有低于40分钟的,且完成课外作业时间低于60分钟的学生数占被调查人数的10%.现将抽查结果绘制成了一个不完整的频数分布直方图,如图所示.
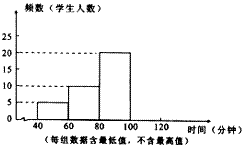 ⑴这次被抽查的学生有 人;
⑴这次被抽查的学生有 人;
⑵请补全频数分布直方图;
⑶被调查这些学生每天完成课外作业时间的中位数在 组(填时间范围);
⑷若该校共有3600名学生,请估计该校大约有多少名学生每天完成课外作业时间在80分钟以上(包括80分钟).
(改编)
21.(本小题满分8分)
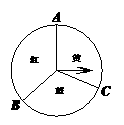
如图,将一个转盘3等份,并在每一份内注上“红、蓝、黄”标记. 小明和小亮用这个转盘进行“配紫色”游戏. 游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明赢,否则小亮赢.
⑴若仅转动转盘两次,两次转出的颜色恰好配成紫色,则该事件属于 事件;(填“必然”或“随机”)
⑵你认为谁获胜的概率大?请通过“画树状图”或“列表”的方法加以分析说明.
20.(本小题满分8分)
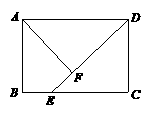
如图,矩形ABCD中,点E是BC上一点,AD=DE,AF⊥DE,垂足为F.
求证:AF=AB.
19.解答下列各题(本题有2小题,第(1),(2)小题每题4分,共8分.)
⑴计算:(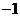 )2009-(
)2009-(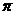 -
-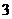 )0+
)0+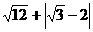 .
.
⑵先化简,再求值: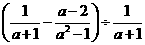 ,其中
,其中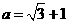 .
.
18.如图,矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的周长为 _.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com