
题目列表(包括答案和解析)
14.雪岩在八年级下学期的数学成绩如下表所示
|
测
试类别 |
平 时 |
期 中考 试 |
期 末 考 试 |
|||
|
测验1 |
测验2 |
测验3 |
课 题学 习 |
|||
|
成绩 |
88 |
70 |
98 |
86 |
90 |
87 |

(1) 计算该学期的平时平均成绩.
(2) 如果学期的总评成绩是根据扇形统计图所示的权重计算,请计算出雪岩在 该学期的总评成绩.
[试题来源]改编自2008年中考题.
[命题意图]①考察学生算术平均数与加权平均数的应用能力.
②以扇形统计图形式展示权重,既考核了平均数知识又体现识别统计图能力.
③解决有关统计图的问题关键在于“读图”,理解图象中所蕴含的信息.
[参考答案](1)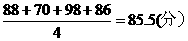
(2)85.5×10%+90×30%+87×60%=87.75(分)
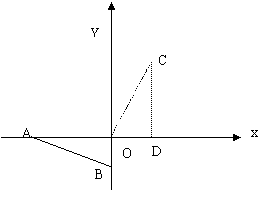
12.如图,在直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴负 半轴、y轴的负半轴上,且OA=2,OB=1,将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移一个单位,得△CDO。
(1)在坐标系中画出△CDO,并写出点A、C的坐标;
(2)若一个二次函数的图像经过(1)中的A、B、D三点,
求出此二次函数的关系式。
[试题来源]原创
[命题意图]①考察学生的平移、旋转等简单图形变换的能力和运用待定系数法确定二次 函数关系式的能力。
②本题特点:对于所求的二次函数关系式,既可以设两点式,也可以设一般式。
③讲评时给学生总结求二次函数关系式一般常识:已知与X轴两交点坐标则设两点式;否则设一般式.
[参考答案](1)作图如图所示。A(-2,0),C(1,2)
(2)由已知得:点B坐标为(0,-1),点D坐标为(1,0)
①设二次函数关系式为y=ax2+bx+c ,由题意得:
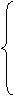 4a-2b+c=0
解得a=
4a-2b+c=0
解得a=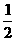 ,b=
,b=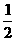 ,
,
a+b+c=0
所以y=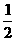 x2+
x2+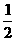 x-1
x-1
c=-1,
②设二次函数关系式为y=a(x-x1)(x-x2),即y=a(x+2)(x-1)
将点B(0,-1)代入y=a(x+2)(x-1)得a=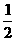 ,
,
所以y=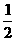 (x+2)(x-1),即y=
(x+2)(x-1),即y=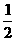 x2+
x2+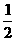 x-1
x-1
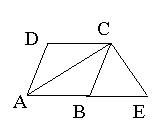 13.如图,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC且与AB的延长线交与点E.求证:四边形AECD是等腰梯形.
13.如图,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC且与AB的延长线交与点E.求证:四边形AECD是等腰梯形.
[试题来源]八(上)《学习手册》
[命题意图]①检验学生对等腰梯形判定方法的掌握情况.
②将等腰梯形问题与菱形相结合,在考核学生
梯形知识的同时又考察了菱形有关性质.
③学生在证明四边形为等腰梯形时,常直接
找所 需条件:同一底上的两底角相等或两
条腰相等, 而常忽略一关键要素:已经证
明该四边形为 梯形了吗?
[参考答案]证明:∵DC∥AB(AE),且AD不平行于EC∴四边形AECD是梯形
由菱形性质知:∠BAC=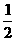 ∠BAD=30°,且CE⊥AC
∠BAD=30°,且CE⊥AC
∴∠E=∠BAD=60°则梯形AECD是等腰梯形。
10.(1)计算︱-2︱+(π-3)0-(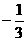 )-2+(-1)2009
)-2+(-1)2009
[试题来源]原创
[命题意图]①考察学生有理数混合运算能力。
②本题将学生易出错的几种情况全部包含在内。
③注意从左到右的运算顺序,谨防“-(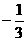 )-2”的结果出错,计算时应根据题目的结构特点寻求合理、简捷的运算途径.
)-2”的结果出错,计算时应根据题目的结构特点寻求合理、简捷的运算途径.
[参考答案]解:原式=2+1-9-1
=-7
(2)解方程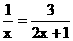
[试题来源]原创
[命题意图]①本题主要考查分式方程的解法、方程解的意义、必须要验根等知识.
②根据师总结经验,一部分学生学习分式方程相当长时间仍存在几种错误:求的是错解代入公分母却未代入方程两边看是否相等;代入公分母检验时发生错误浑然不知。
[参考答案]解:方程两边同乘以x(2x+1)得:2x+1=3x 解得 x=1
检验:当x=1时 x(2x+1)=1×3=3 ≠0 ∴ x=1是原方程的解
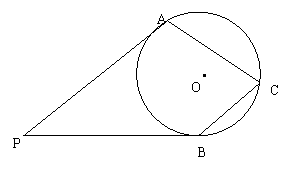 11.如图,PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点,若∠APB=40°,求∠ACB的度数.
11.如图,PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点,若∠APB=40°,求∠ACB的度数.
[试题来源]2008年中考题。
[命题意图]①考察学生对切线与圆特殊位置关系
的认识,圆周角与圆心角之间关系
的应用。
②讲评时要让学生明白遇圆
切线问题常作过切点半径。
利用四边形APBO求出圆周角度数,关键是圆周角与圆心
角之间的关系。
[参考答案]解:连接OA、OB,则OA⊥PA,OB⊥PB,∠PAO=∠PBO=90°,
∠AOB=360°-∠PAO-∠PBO-∠APB=360°-90°-90°-40°
=140°
∠ACB=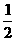 ∠AOB=
∠AOB=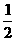 ×140°=70°
×140°=70°
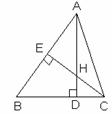
9、如图:△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: ,使△ABD≌△CEB。
[试题来源]七年级(下)教材
 [命题意图]①考核学生对三角形全等判定方法的掌握情况.
[命题意图]①考核学生对三角形全等判定方法的掌握情况.
②本题答案不惟一,对学生熟悉定理的情况及识 图能力提出了较高要求.
③图中隐含条件∠B=∠B,且有∠CEB=∠ADB=90°,
此时想到“ASA” 、“AAS”两种判定方法。
[参考答案]①BD=BE ②AD=CE ③BA=BC
8.不等式组 的解集是 .
x-1>4x-10
[试题来源]原创
[命题意图]①考察学生解不等式的能力及根据图象确定不等式组解集的方法。
②讲评时,可去掉其中一个不等式,以给定的解集,让学生补充符合条件的不等式。
[参考答案]x<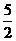
7.在一个袋子中装有除颜色外其它均相同的2个红球和3个白球,从中任意摸出一个球,则摸到红球的概率是 .
[试题来源]原创
[命题意图]①考察学生概率统计的基础知识。
②该题较为简单,师讲评该题时可适当结合本试卷15题拓展延伸。
[参考答案]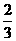
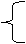 3x-6<4-x
3x-6<4-x
6.下列每个图是由若干个圆点组成的形如四边形的图案.当每条边(包括顶点)上有n(n≥2)个圆点时,图案的圆点数为Sn,按此规律推断Sn关于n的关系为: .
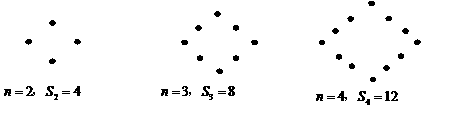

[试题来源]2008年中考题。
[命题意图]①根据所给图形,找蕴含在两个变量Sn与n之间的关系,考察学生观察事物与探索规律的能力。
②本题是一道考查学生观察、推理和猜想能力的猜想题,既可采用直接观察的方法;又可发现,随着n每增大1,Sn必增大4,即Sn与n之间存在一次函数关系,用待定系数法也可确定Sn与n之间的关系。
③师应向学生讲明白:解本题的关键是结合图形,找出Sn与n之间存在的规律,解类似问题的一般思路是观察-猜想-探索规律-验证.
[参考答案]Sn=4(n-1)
5.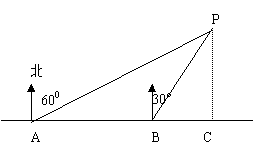 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°的方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°的方向上,则灯塔P到环海路的距离PC= 米(用根号表示).
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°的方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°的方向上,则灯塔P到环海路的距离PC= 米(用根号表示).
[试题来源]2008年中考题。
[命题意图]①在直角三角形中,结合三角函数知识,用所求的边表示出需用的边。
②本题渗透了消元化归思想:求PC,用PC表示出AC与BC,顺理成章找到了AB与PC之间的关系。
③师向学生讲清:在解这一类实际应用问题时,首先要构造适当的直角三角形,再将题目中提供的信息和需要求得的结果与直角三角形中的元素对应,从而将问题转化为解直角三角形问题.
[参考答案]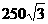
4.若分式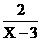 有意义,则X应满足的条件是( )
有意义,则X应满足的条件是( )
A.X≠0 B.X≥3 C.X≠3 D.X≤3
[试题来源]原创
[命题意图]①考察学生对分式基本性质的理解。
②师在评讲该例时应将分式有意义、值为0、值不为0几种情况加以对比。
[参考答案]C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com