
题目列表(包括答案和解析)
3、已知一次函数y=kx+b,当-3≤x≤1时,对应y的值为1≤y≤9.则k·b的值( )
(A)14 (B)-6
(C) -6或21 (D) -6或14
[命题意图]考查一次函数的增减性,试题亮点是渗透了分类讨论思想,许多学生没有进行分类求解,选A或B
[参考答案]D
[试题来源]原创题
2、如图,圆柱形开口杯底部固定在长方体水池底,向水池匀速注入水(倒在杯外),水池中水面高度是h,注水时间为t,则h与t之间的关系大致为下图中的 ( )
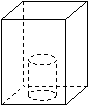
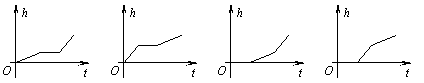
A B C D
[命题意图]探索具体问题中的数量关系和变化规律类问题,考纲要求D级灵活运用,这类问题情境来源于生活,如龟兔赛跑,乌鸦喝水等,重视对学生学习数学知识与技能的结果和过程的评价。
[参考答案] B
[试题来源]改编题
1、下列实数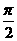 ,sin30°,0.1414,
,sin30°,0.1414,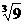 ,0.383383338…… , 22/7中,无理数的个数是
,0.383383338…… , 22/7中,无理数的个数是
A、2个 B、3个 C、4个 D、5个
[命题意图]考查学生对无理数的认识,无理数的概念比较抽象,讲评时,要求学生了解常见无理数的四种形式。
常见无理数:含有π的的式子
根号形(开方开不尽的)
构造型
三角函数形(值不是有理数)
[参考答案] B
[试题来源]原创题
1.据悉,超级磁力风力发电机可以大幅度提升风力发电效率,但其造价高昂,每座磁力风力发电机,其建造花费估计要5300万美元,“5300万”用科学记数法可表示为 ( )
A.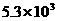 B.
B.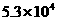 C.
C.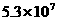 D.
D.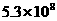
[命题意图]在现实背景下考查学生对科学记数法的理解及百、千、万、亿等与数之间的互化。
3.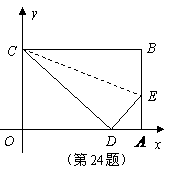 如图,四边形
如图,四边形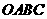 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点 在
在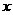 轴上,点
轴上,点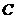 在
在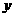 轴上,将边
轴上,将边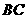 折叠,使点
折叠,使点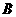 落在边
落在边 的点
的点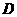 处.已知折叠
处.已知折叠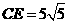 ,且
,且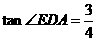 .
.
(1)判断 与
与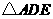 是否相似?请说明理由;
是否相似?请说明理由;
(2)求直线 与
与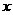 轴交点
轴交点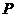 的坐标;
的坐标;
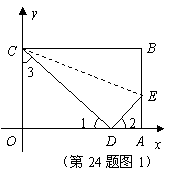 (3)是否存在过点
(3)是否存在过点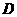 的直线
的直线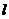 ,使直线
,使直线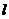 、直线
、直线 与
与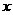 轴所围成的三角形和直线
轴所围成的三角形和直线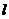 、直线
、直线 与
与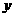 轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
答案:解:(1) 与
与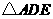 相似.
相似.
理由如下:
由折叠知,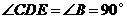 ,
,
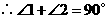 ,
,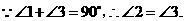
又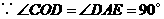 ,
,
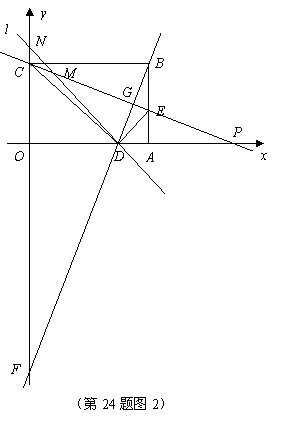
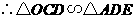 .
.
(2)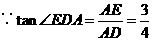 ,
, 设
设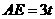 ,
,
则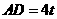 .
.
由勾股定理得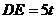 .
.
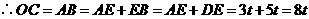 .
.
由(1)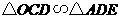 ,得
,得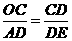 ,
,
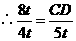 ,
,
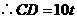 .
.
在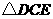 中,
中,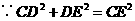 ,
,
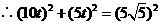 ,解得
,解得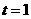 .
.
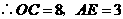 ,点
,点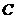 的坐标为
的坐标为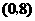 ,
,
点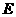 的坐标为
的坐标为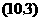 ,
,
设直线 的解析式为
的解析式为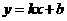 ,
,
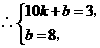 解得
解得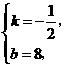
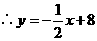 ,则点
,则点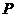 的坐标为
的坐标为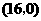 .
.
(3)满足条件的直线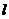 有2条:
有2条: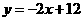 ,
,
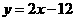 .
.
如图2:准确画出两条直线.
本题考查了四边形、坐标系、一次函数、三角函数知识,特色是将多个知识点糅合在一起,考察学生的综合应用能力、想象能力、是否存在问题的解决能力,对学生的能力要求比较高,讲解时一要把这几块知识都梳理一遍二要注意知识之间存在哪些联系。
本资料由《七彩教育网》 提供!
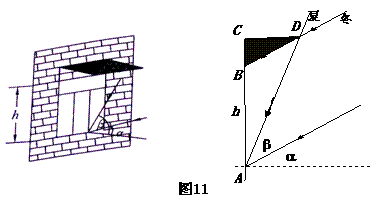
2、(2007湖北)州政府投资3个亿拟建的恩施民族高中,它位于北纬31°,教学楼窗户朝南,窗户高度为h米,此地一年的冬至这一天的正午时刻太阳光与地面的夹角最小为α,夏至这一天的正午时刻太阳光与地面的夹角最大为 β.若你是一名设计师,请你为教学楼的窗户设计一个直角形遮阳蓬BCD,要求它既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内(如图11).根据测量测得∠α=32.6°,
∠β= 82.5°,h=2.2米.请你求出直角形遮阳蓬BCD中BC与CD的长各是多少?(结果精确到0.1米)
(参考数据:sin32.6°=0.54,sin82.5°=0.99,tan32.6°=0.64,tan82.5°=7.60)
答案:解:由题意得,∠BDC=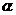 ,∠ADC=
,∠ADC=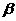
在Rt∆BCD中,tan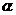 =
=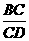 ①
(2分)
①
(2分)
在Rt∆ADC中,tan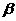 =
=
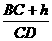 ②
(4分)
②
(4分)
由①、②可得: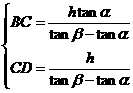 (7分)
(7分)
把h=2.2,tan32.6°=0.64,tan82.5°=7.60代入上式,得
BC≈0.2(米),CD≈0.3(米) (9分)
所以直角遮阳蓬BCD中BC与CD的长分别是0.2米和0.3米 (10分)
(其他解法,参照此标准评分)
锐角三角函数是中考命题的基本内容,中考对这部分知识的考查题型多样,多以中、低档的填空题和选择题为主,个别省市也有小型综合题和创新题,几乎每份试卷都有一道实际应用题出现,要善于把生活问题转化为有关的数学问题来求解。
1.(2007济宁市)先化简,再求值: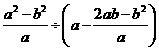 ,其中
,其中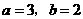 。
。
答案:解:原式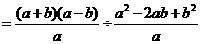
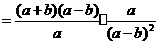
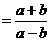 .····················································································································· 6分
.····················································································································· 6分
当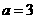 ,
,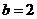 时,
时,
原式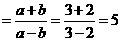 .···························································································· 8分
.···························································································· 8分
本题主要考察了分式运算及学生运算能力,本题特色是让学生自己选择数带入计算,这要照顾到方式是否有意义情况,讲解时强调在通分时不要漏乘。
4.(2007常州)二次函数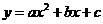 的部分对应值如下表:
的部分对应值如下表:
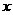 |
… |
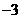 |
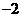 |
 |
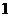 |
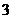 |
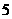 |
… |
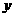 |
… |
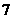 |
 |
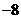 |
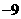 |
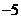 |
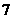 |
… |
二次函数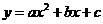 图象的对称轴为
图象的对称轴为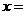 ,
,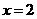 对应的函数值
对应的函数值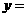 .
.
答案:1,-8 函数不仅是一种重要的数学知识,而且还是一种重要的数学思想,它是贯穿初中代数的一条主线。而二次函数是函数中的重点,也是初中代数的重点和难点。抛物线上纵坐标相等的两个点(m,p),(n,p)是关于抛物线对称轴对称的两个点,由(m,p),(n,p)可求该抛物线的对称轴为x=(m+n)/2.
3.(2007安顺市)如图1,已知正方形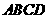 的边长为3,如果将线段
的边长为3,如果将线段 绕点
绕点 旋转后,点
旋转后,点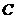 落在
落在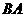 延长线上的
延长线上的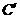 点处,那么
点处,那么
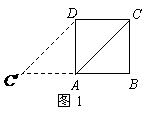
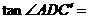 .
.
答案: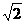 解此类问题的关键是在掌握锐角三角函数的意义的基础上建立数学模型,构造直角三角形求解。
解此类问题的关键是在掌握锐角三角函数的意义的基础上建立数学模型,构造直角三角形求解。
2.(2007济南市)分解因式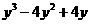 的结果为 .
的结果为 .
答案:y(y-2)2提公因式法分解因式的关键是确定公因式,确定公因式的方法是:“以各项系数的最大公约数与相同字母的最低次幂的积”。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com