
题目列表(包括答案和解析)
2.据2009年2月1日中央电视台“朝闻天下”报道,我市目前汽车拥有量约为3 100 000辆.则3 100 000用科学记数法表示为 …………………………………………[ ]
A.0.31×107 B.31×105
C.3.1×105 D.3.1×106
只有一项是符合题目要求的)
1.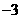 的倒数是…………………………………………………………………………[ ]
的倒数是…………………………………………………………………………[ ]
A.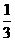 B.
B.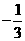 C.
C.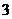 D.
D.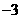
9、计算:


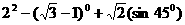

命题意图:基本运算能力是数学科的重要要求,考查学生基本运算能力必不可少,年年考。通过此题考查学生涉及知识点是比较多的,有乘方 特殊角三角函数值 二次根式运算等。
答案:5
试题来源:自编
10如图,在△ABC与△ABD中,BC=BD.设点E是BC的中点,点F是BD的中点.
(1)请你在图中作出点E和点F;(要求用尺规作图,保留作图痕迹,不写作法与证明)
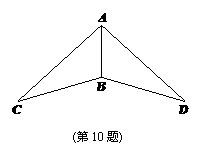 (2)连接AE,AF.若∠ABC=∠ABD,请你证明△ABE≌△ABF.
(2)连接AE,AF.若∠ABC=∠ABD,请你证明△ABE≌△ABF.
命题意图:掌握知识同时要培养学生的能力,尺规作图就是考查的动手能力,三角形全等的证明是几何证明的基础,考查是必要的。
答案:中点作法用作垂直平分线的方法,三角形全等利用边角边定理
试题来源:08年中考题
7、已知m是方程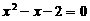 的一个根,则代数式
的一个根,则代数式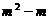 的值等于
.
的值等于
.
命题意图:考查学生对于问题解决的灵活性,做题不能死板教条,观察问题的特征,采取适当方法。考查学生对方程的根的概念和整体思想了解情况。
答案:2
试题来源:08年中考题
8第一个数,第二个数,第三个数,第四个数分别为1,1+2,1+2+3,1+2+3+4,则第N个数的结果为
--------------------------------------
命题意图:培养学生的能力是教学一个目标,通过此题考查学生对于规律的探究能力。
答案: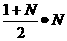
试题来源:自编
5、在函数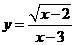 中,自变量
中,自变量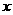 的取值范围是______________
的取值范围是______________
命题意图:考查学生考虑问题是否全面。代数式有意义的条件,既要考虑分子,又要考虑分母。
答案: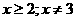
试题来源:自编
6;分解因式:
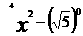

.命题意图:考查学生对于在新的情境下应变能力,以及能否利用公式进行因式分解。
答案:(X-1)(X+1)
试题来源:自编
4、下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是( )

A B C D
命题意图:能对图形进行分解和组合,考查学生想象能力和动手能力,
答案:B
试题来源:08年中考题
2.从一副未曾启封的扑克牌中取出2张红桃,3张黑桃的牌共5张,洗匀后,从这5张牌中任取1张牌恰好是黑桃的概率是( )
A.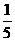 B.
B.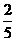 C.
C.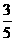 D.1
D.1
命题意图:学习知识是为了应用知识,本题考查概率知识的简单应用,同时加深了学生对数学实用性认识,增加学习的积极性。
答案:C
试题来源:自编
3下列哪一个数与方程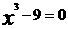 的根最接近(
)
的根最接近(
)
A 1 B 2 C 3 D4
命题意图:通过不同形式来考查学生对立方根的表示和数的估算能力。
答案B
试题来源:自编
1.数据1,1,2,2,3,3,4的极差是( )
A.1 B.2 C.3 D.6
命题意图:基础知识的考查包括对基本概念考查,本题目的考查学生对极差概念理解。
答案:C
试题来源:自编
23.(本小题满分10分)
模型拓展一:(1)1+5=6
(2)1+5×9=46
(3)1+5(n-1)
模型拓展二:(1)1+m
(2)1+m(n-1)
问题解决:(1)在不透明口袋中放入18种颜色的小球(小球除颜色外完全相同)各40个,现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?
(2)1+18×(10-1) =163
 18.(浙江省2008)如图,在平面直角坐标系中,已知点
18.(浙江省2008)如图,在平面直角坐标系中,已知点 坐标为(2,4),直线
坐标为(2,4),直线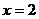 与
与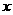 轴相交于点
轴相交于点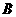 ,连结
,连结 ,抛物线
,抛物线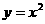 从点
从点 沿
沿 方向平移,与直线
方向平移,与直线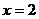 交于点
交于点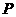 ,顶点
,顶点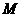 到
到 点时停止移动.
点时停止移动.
(1)求线段 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点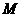 的横坐标为
的横坐标为 ,
,
①用 的代数式表示点
的代数式表示点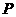 的坐标;
的坐标;
②当 为何值时,线段
为何值时,线段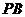 最短;
最短;
(3)当线段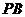 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点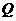 ,使△
,使△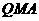
的面积与△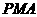 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点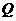 的坐标;若
的坐标;若
不存在,请说明理由.
解:(1)设 所在直线的函数解析式为
所在直线的函数解析式为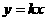 ,
,
∵ (2,4),
(2,4),
∴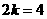 ,
, 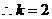 ,
,
∴ 所在直线的函数解析式为
所在直线的函数解析式为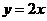 .
.
(2)①∵顶点M的横坐标为 ,且在线段
,且在线段 上移动,
上移动,
∴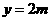 (0≤
(0≤ ≤2).
≤2).
∴顶点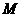 的坐标为(
的坐标为( ,
, ).
).
∴抛物线函数解析式为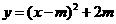 .
.
∴当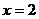 时,
时,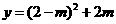
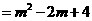 (0≤
(0≤ ≤2).
≤2).
∴点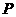 的坐标是(2,
的坐标是(2,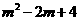 ).
).
② ∵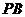 =
=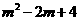 =
=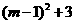 , 又∵0≤
, 又∵0≤ ≤2,
≤2,
∴当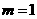 时,PB最短.
时,PB最短.
(3)当线段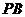 最短时,此时抛物线的解析式为
最短时,此时抛物线的解析式为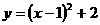 .
.
假设在抛物线上存在点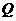 ,使
,使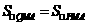 .
.
设点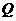 的坐标为(
的坐标为(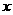 ,
,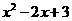 ).
).
①当点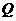 落在直线
落在直线 的下方时,过
的下方时,过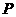 作直线
作直线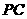 //
// ,交
,交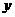 轴于点
轴于点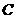 ,
,
∵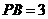 ,
,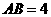 ,
,
∴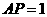 ,∴
,∴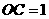 ,∴
,∴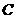 点的坐标是(0,
点的坐标是(0,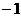 ).
).
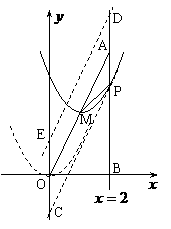 ∵点
∵点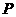 的坐标是(2,3),∴直线
的坐标是(2,3),∴直线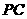 的函数解析式为
的函数解析式为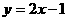 .
.
∵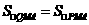 ,∴点
,∴点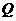 落在直线
落在直线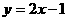 上.
上.
∴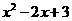 =
=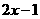 .
.
解得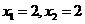 ,即点
,即点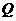 (2,3).
(2,3).
∴点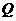 与点
与点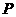 重合.
重合.
∴此时抛物线上不存在点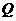 ,使△
,使△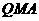 与△
与△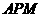 的面积
的面积
相等.
②当点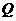 落在直线
落在直线 的上方时,
的上方时,
作点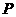 关于点
关于点 的对称称点
的对称称点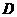 ,过
,过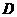 作直线
作直线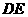 //
// ,交
,交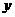 轴于点
轴于点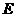 ,
,
∵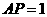 ,∴
,∴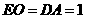 ,∴
,∴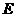 、
、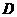 的坐标分别是(0,1),(2,5),
的坐标分别是(0,1),(2,5),
∴直线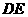 函数解析式为
函数解析式为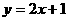 .
.
∵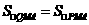 ,∴点
,∴点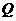 落在直线
落在直线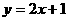 上.
上.
∴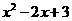 =
=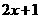 .
.
解得: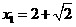 ,
,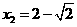 .
.
代入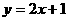 ,得
,得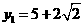 ,
,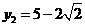 .
.
∴此时抛物线上存在点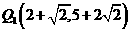 ,
,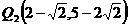
使△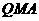 与△
与△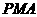 的面积相等.
的面积相等.
综上所述,抛物线上存在点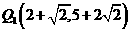 ,
,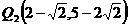
使△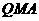 与△
与△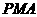 的面积相等.
的面积相等.
本资料由《七彩教育网》 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com