
题目列表(包括答案和解析)
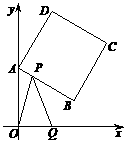
26.如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.
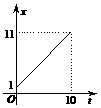
(1) 当P点在边AB上运动时,点Q的横坐标 (长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2) 求正方形边长及顶点C的坐标;
(3) 在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.


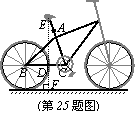
25.如图所示是一辆自行车的侧面示意图.已知车轮直径为65cm,车架中AC的长为42cm,座杆AE的长为18cm,点E、A、C在同一条直线上,后轴轴心B与中轴轴心C所在直线BC与地面平行,∠C=73°.求车座E到地面的距离EF(精确到1cm).(参考数据:sin73°≈0.96,cos73°≈0.29,tan73°≈3.27.)
24.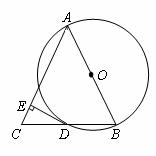 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若⊙O的半径为5,∠BAC=60°,求DE的长.
23.“5·12”四川汶川大地震的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区.已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点.从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1) 请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
|
|
C |
D |
总计 |
|
A |
|
|
200吨 |
|
B |
x吨 |
|
300吨 |
|
总计 |
240吨 |
260吨 |
500吨 |
(2) 设A、B两个蔬菜基地的总运费为w元,写出w与x之间的函数关系式,并求总运费最小的调运方案;
(3)
经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少 元(
元( >0),其余线路的运费不变,试讨论总运费最小的调运方案.
>0),其余线路的运费不变,试讨论总运费最小的调运方案.
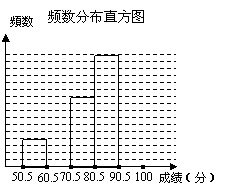
22. 一所中学,为了让学生了解环保知识,增强环保意识,特地举行了一次“保护家乡”的环保知识竞赛,共有900名学生参加这次竞赛.为了解本次竞赛的情况,从中抽取了部分学生的成绩(得分均为正整数,满分为100分)进行统计.
|
分组 |
频数 |
频率 |
|
50.5-60.5 |
4 |
0.08 |
|
60.5-70.5 |
8 |
0.16 |
|
70.5-80.5 |
10 |
0.20 |
|
80.5-90.5 |
16 |
0.32 |
|
90.5-100 |
|
|
|
合计 |
|
|
 频率分布表
频率分布表
请根据上表和图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频数分布直方图;
(3)在该问题中,样本容量是___________;
(4)全体参赛学生中,竞赛成绩的中位数落在哪个组内?
(5)若成绩在90分以上(不含90分)可以获奖,在全校学生的试卷中任抽取一张,获奖的概率是多大?
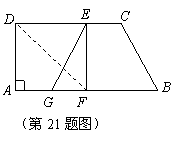
21. 如图,在直角梯形纸片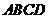 中,
中,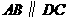 ,
,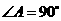 ,
,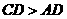 ,将纸片沿过点
,将纸片沿过点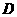 的直线折叠,使点
的直线折叠,使点 落在边
落在边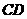 上的点
上的点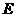 处,折痕为
处,折痕为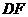 .连接
.连接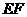 并展开纸片.
并展开纸片.
(1)求证:四边形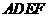 是正方形;
是正方形;
(2)取线段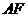 的中点
的中点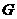 ,连接
,连接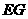 ,如果
,如果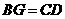 ,试说明四边形
,试说明四边形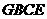 是等腰梯形.
是等腰梯形.
20.解不等式组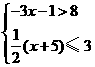 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
19.先化简,再求值: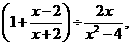 并代入你喜欢且有意义的x值。
并代入你喜欢且有意义的x值。
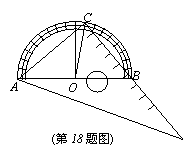
18.小刚有一块含有30°角的直角三角板,他想测量其短直角边的长度,而手中另外只有一个量角器,于是他采用了如下的办法,并获得了相关数据:
第一步,他先用三角板标有刻度的一边测出量角器的直径AB的长度为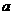 cm;
cm;
第二步,将三角板与量角器按如图所示的方式摆放,并量得∠BOC为
2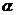 (O为AB的中点).
(O为AB的中点).
则三角板的短直角边AC的长为 .
17.对于大于或等于2的自然数n的平方进行如下“分裂”,分裂成n个连续奇数的和,则自然数7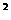 的分裂数中最大的数是 ,自然数n
的分裂数中最大的数是 ,自然数n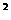 的分裂数中最大的数是 .
的分裂数中最大的数是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com