
题目列表(包括答案和解析)
19. (本题满分7分)
(本题满分7分)
解:方案一: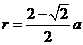 -1分-
-1分-
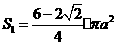 -2分-
-2分-
方案二: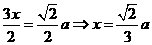 -3分-
-3分-
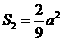 -4分-
-4分-
方案三: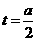 -5分-
-5分-
方案四: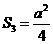 -6分-
-6分-
通过比较大小得: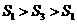 ,故选择方案一.
-7分-
,故选择方案一.
-7分-
18.(本题满分7分)
(1) 解:原式=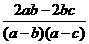 -1分-
-1分-
=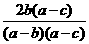 -2分-
-2分-
=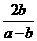 -3分-
-3分-
(2) 解: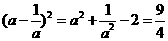 -2分-
-2分-
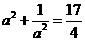 -4分-
-4分-
26.(本题满分13分) 某同学现利用同一材料进行探究数学问题:
(1)若它将此材料制成三角形,如图(f),DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,求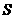 △DMN∶
△DMN∶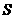 四边形ANME 的值?请写明详细的过程;
四边形ANME 的值?请写明详细的过程;
(2)现在,他将此材料制成梯形ABCD,AD∥BC,EF为等腰梯形梯形的中位线,(如图(g)),G为EF的中点,若(1)中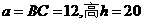 ,
,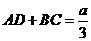 ,问:当AD的值为多大时,
,问:当AD的值为多大时,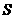 △EGH∶
△EGH∶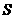 五边形AHGFD的比值最大,最大值为多少?
五边形AHGFD的比值最大,最大值为多少?
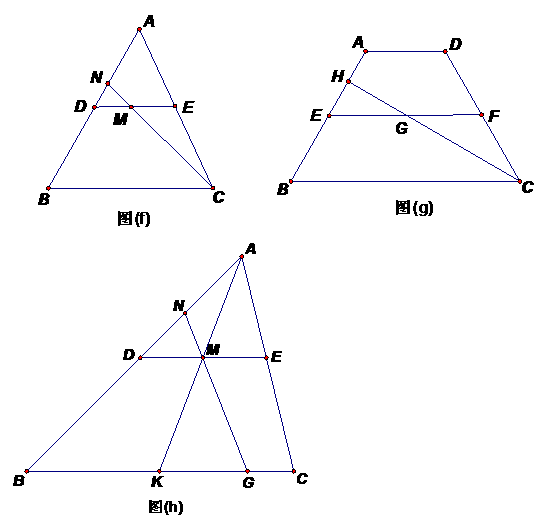 (3)如图(h),若在BC边上存在一动点G,G为BC边的
(3)如图(h),若在BC边上存在一动点G,G为BC边的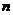 等分点,
等分点,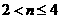 ,DE为△ABC的中位线,M为DE中点,连结AM交BC于K,. 问:当
,DE为△ABC的中位线,M为DE中点,连结AM交BC于K,. 问:当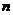 的值为多大时,
的值为多大时,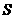 △DMN∶
△DMN∶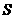 四边形ANME 的值存在最小值,说明理由.
四边形ANME 的值存在最小值,说明理由.










[答案]
25.(本题满分12分) 如图,AB是⊙O的直径. AC是⊙O上一条弦,AC在AB下方,在⊙O上存在一点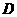 .
.
(1)当D点在O点在正上方(如图(a)),连结AD、CD、BC、BD,CD交AB于E,则,在图中你可以发现多少对相似三角形?请列举出来,并说明理由.
(2)①当D点在劣弧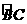 上运动(不与B、C重合)则
上运动(不与B、C重合)则
AD
AC(在横线上填写“>”、 “<”或“=”)并说明理由;
②当D点在劣弧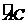 上运动(不与A、C重合)则
上运动(不与A、C重合)则
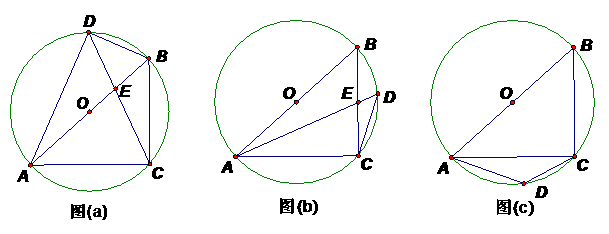 AD AC(在横线上填写“>”、 “<”或“=”)并说明理由;
AD AC(在横线上填写“>”、 “<”或“=”)并说明理由;





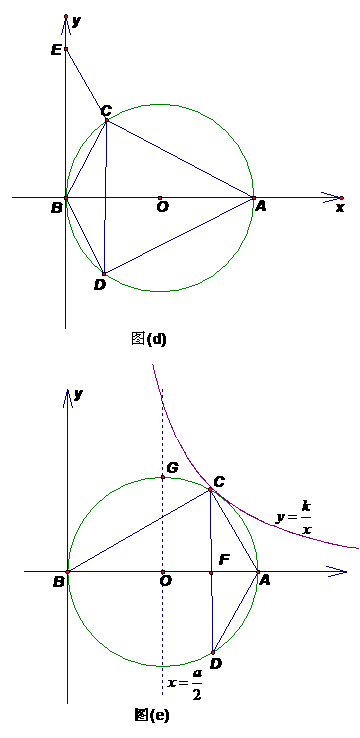
(3)①如图(d), 以B点为原点,AB所在的直线为x轴,建立平面直角坐标系,∠DCA=∠CBA=60°,连结BD,过C点作CE∥DB,求证:四边形CDBE为平行四边形;
②若C点在劣弧 上运动(不与A、G重合),过C点作CD垂直于x轴于F(如图(e)),
上运动(不与A、G重合),过C点作CD垂直于x轴于F(如图(e)), ,
, , C点在函数
, C点在函数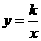 上,设△BCA的面积为s,且s=1+. n是小于20的整数,且k≠,求BC2的最小值.
上,设△BCA的面积为s,且s=1+. n是小于20的整数,且k≠,求BC2的最小值.




















24.(本题满分12分) 某校数学研究性学习小组准备设计一种高为60cm的简易废纸箱.如图1,废纸箱的一面利用墙,放置在地面上,利用地面作底,其它的面用一张边长为60cm的正方形硬纸板围成.经研究发现:由于废纸箱的高是确定的,所以废纸箱的横截面图形面积越大,则它的容积越大.
(1)该小组通过多次尝试,最终选定下表中的简便且易操作的三种横截面图形,如图2,是根据这三种横截面图形的面积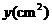 与
与 (见表中横截面图形所示)的函数关系式而绘制出的图象.请你根据有信息,在表中空白处填上适当的数、式,并完成
(见表中横截面图形所示)的函数关系式而绘制出的图象.请你根据有信息,在表中空白处填上适当的数、式,并完成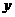 取最大值时的设计示意图;
取最大值时的设计示意图;
|
横截面图形 |
|
|
|
 与 与 的函数关系式 的函数关系式 |
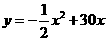 |
|
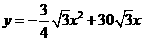 |
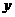 取最大值时 取最大值时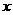 (cm)的值 (cm)的值 |
30 |
|
20 |
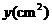 取得的最大值 取得的最大值 |
 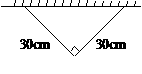 450 450 |
|
 |
 取最大值时的设计示意图 取最大值时的设计示意图 |
|
 |
 |

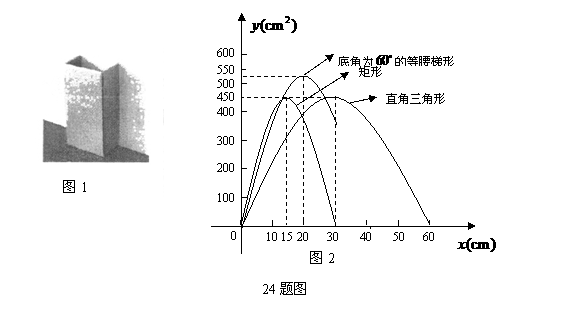 (2)在研究性学习小组展示研究成果时,小华同学指出:图2中“底角为
(2)在研究性学习小组展示研究成果时,小华同学指出:图2中“底角为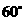 的等腰梯形”的图象与其他两个图象比较,还缺少一部分,应该补画.你认为他的说法正确吗?请简要说明理由.
的等腰梯形”的图象与其他两个图象比较,还缺少一部分,应该补画.你认为他的说法正确吗?请简要说明理由.








23.(本题满分10分) 已知方程组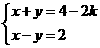 的解满足
的解满足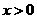 ,且
,且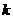 为整数.
为整数.
(1)求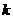 的取值范围;
的取值范围;
(2)若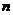 是正整数,试比较代数式
是正整数,试比较代数式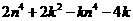 的值与0的大小.
的值与0的大小.








22.(本题满分10分) 如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后B点与P点重合.
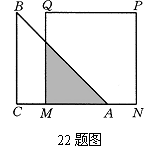 (1)试写出重叠部分面积ycm2与MA长度x cm之间的函数关系式;
(1)试写出重叠部分面积ycm2与MA长度x cm之间的函数关系式;
(2)在平面直角坐标系中绘制出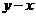 的函数图像;
的函数图像;
(3)若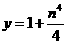 ,
,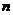 为正整数,求
为正整数,求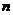 的最大值。
的最大值。

21.(本题满分10分) 数学是一门艺术与美妙结合的一门学科,现在做一次探究:
观察下图的图形,这是通过等边三角形绘制的一幅自相似图形.





边长为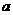 的等边三角形
的等边三角形 经过第1次变换得到
经过第1次变换得到 ,经过第2次变换得到
,经过第2次变换得到

………………
[提出问题]经过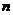 次变换,在图形中可数得多少个三角形?
次变换,在图形中可数得多少个三角形?
[解决问题](1)填写下列表格:
|
|
第1次 |
第2次 |
第3次 |
第4次 |
………… |
第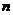 次 次 |
 |
 |
 |
 |
 |
………… |
|
 |
|
|
|
|
………… |
|
(2)根据上面的列表,你得到了什么规律,请说明:

(3)根据你的判断,经过第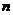 次变换后,三角形的个数是
.
次变换后,三角形的个数是
.
20.(本题满分8分) 已知方程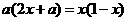 的两实数根为
的两实数根为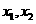 ,设
,设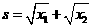 ,
,
(1)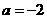 时,求
时,求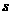 的值;(2)若
的值;(2)若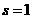 ,求
,求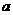 的取值范围.
的取值范围.


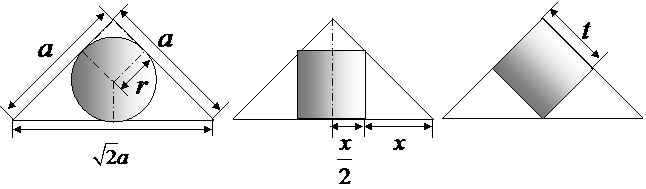
19.(本题满分7分) :张师傅分别在一张边长为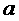 的等腰三角形里制作圆、正方形,构思图如下:
的等腰三角形里制作圆、正方形,构思图如下:


则三种方案中面积最大的是哪种方案?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com