
题目列表(包括答案和解析)
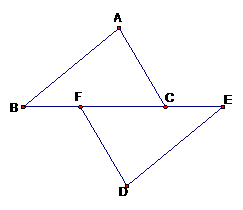
4、如图.点B,F,C,E在同一条直线上,点A,D在直线BE的两侧,AB∥DE,AC∥DF,BF=CE.求证:AC=DF.
3、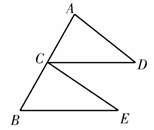 如图,点
如图,点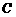 是
是 的中点,
的中点,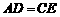 ,
,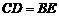 .
.
求证:△ ≌△
≌△
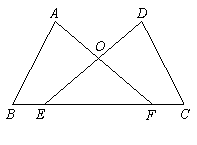
2、如图,四边形ABCD的对角线AC、BD相交于点O,△ABC≌△BAD.
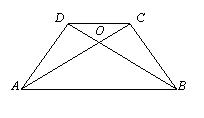 求证:(1)OA=OB;(2)AB∥CD.
求证:(1)OA=OB;(2)AB∥CD.
1、如图,在 中,点
中,点 、
、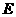 分别在边
分别在边 、
、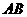 上,
上,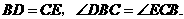 求证:
求证: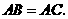
9、等边三角形的判定有: ;
[例题解析]
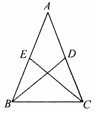
例1:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
 (1)求证:AB=DC;
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
解析:欲证AB=DC,则要看这两线段是否在同一个三角形中,若在,则利用“等角对等边”证之;若不在,则看它们分别分布在哪两个三角形中,然后证全等,从而寻求全等所需的三个条件是解决问题的关键。判断△OEF的形状,在利用(1)的结论时推导出是等腰三角形时,还要考虑是不是直角三角形。证明如下:(1)∵BE=CF,∴BE+EF=CF+EF, 即BF=CE.又∵∠A=∠D,∠B=∠C,∴△ABF≌△DCE(AAS),∴AB=DC.(2)△OEF为等腰三角形 ;理由如下:∵△ABF≌△DCE,∴∠AFB=∠DEC.∴OE=OF.∴△OEF为等腰三角形.
 反思:对于此类证明线段或角的问题,应先从结论出发,分析证明结论所需的条件。再根据条件,选择适合的知识点进行证明。如本题要证明线段相等,根据条件,选择不同的判定,证明的方法、难易度也会因此不同。
反思:对于此类证明线段或角的问题,应先从结论出发,分析证明结论所需的条件。再根据条件,选择适合的知识点进行证明。如本题要证明线段相等,根据条件,选择不同的判定,证明的方法、难易度也会因此不同。
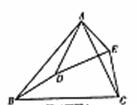
例2 如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE;.
 (1)写出图中两对相似三角形(不得添加字母和线);
(1)写出图中两对相似三角形(不得添加字母和线);
 (2)请分别说明三角形相似的理由.
(2)请分别说明三角形相似的理由.
解析:看图、选择判定方法是解决这类题的关键,已知条件给的都是角,所以选择判定时可以从和角有关的判定入手。解答如下:(1)△ABC∽△ADE;△ABD∽△ACE。(2)①证△ABC∽△ADE,∵∠BAD=∠CAE ,∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE;又∵∠ABC=∠ADE;△ABC∽△ADE;②证△ABD∽△ACE,∵△ABC∽△ADE;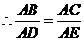
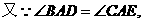
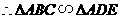
反思:对于此类问题,选择好判定方法是解决这类题的关键,在证明时,应先证简单、把握的,然后现利用已证的结果作条件再应用。
[实弹射击]
8、等腰三角形的“三线合一”是指: 、 、 互相重合。
7、勾股定理是指: 。
6、三角形的内心是 ,它到 的距离相等。
5、三角形的外心是 ,它到 的距离相等。
4、三角形的中位线 第三边,并且 第三边的一半。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com