
题目列表(包括答案和解析)
22.(10分)某超市计划上两个新项目:
项目一:销售A种商品,所获得利润y(万元)与投资金额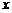 (万元)之间存在正比例函数关系:
(万元)之间存在正比例函数关系: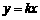 .当投资5万元时,可获得利润2万元;
.当投资5万元时,可获得利润2万元;
项目二:销售B种商品,所获得利润y(万元)与投资金额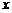 (万元)之间存在二次函数关系:
(万元)之间存在二次函数关系: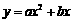 .当投资4万元时,可获得利润3.2万元;当投资2万元时,可获得利润2.4万元.
.当投资4万元时,可获得利润3.2万元;当投资2万元时,可获得利润2.4万元.
⑴ 请分别求出上述的正比例函数表达式和二次函数表达式;
⑵ 如果超市同时对A、B两种商品共投资12万元,请你设计一个能获得最大利润的投资方案,并求出按此方案获得的最大利润是多少?
21.(10分)如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=4,点P是斜边AB上一个动点,点D是CP的中点,延长BD至E,使DE=BD,连结AE.
⑴ 求四边形PCEA的面积;
⑵ 当AP的长为何值时,四边形PCEA是平行四边形;
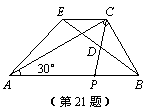 ⑶ 当AP的长为何值时,四边形PCEA是直角梯形.
⑶ 当AP的长为何值时,四边形PCEA是直角梯形.
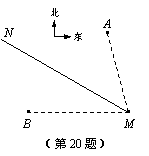
20.(9分)如图,气象部门预报:在海面上生成了一股较强台风,在距台风中心60千米的圆形区域内将会受严重破坏.台风中心正从海岸M点登陆,并以72千米/时的速度沿北偏西60°的方向移动.已知M点位于A城的南偏东15°方向,距A城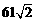 千米;M点位于B城的正东方向,距B城
千米;M点位于B城的正东方向,距B城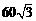 千米.
千米.
假设台风在移动过程中,其风力和方向保持不变,请回答下列问题:
⑴ A城和B城是否会受到此次台风的侵袭?并说明理由;
⑵ 若受到此次台风侵袭,该城受到台风侵袭的持续时间有多少小时?
19.(9分)某高级中学要印制宣传册,联系了甲、乙两家印刷厂.甲厂的优惠条件是:按每份定价1.5元的8折收费,另收900元的制版费;乙厂的优惠条件是:每份定价1.5元的价格不变,而制版费900元则按4折优惠,且甲、乙两厂都规定:一次印刷数量不低于1000份.
⑴ 分别求出两家印刷厂收费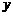 (元)与印刷数量
(元)与印刷数量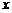 (份)的函数关系式,并指出自变量
(份)的函数关系式,并指出自变量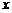 的取值范围;
的取值范围;
⑵ 如何根据印刷数量选择比较合算的方案?如果该中学要印制3000份宣传册,那么应当选择哪家印刷厂?需要多少费用?
18.(9分)某超市有A、B、C三种型号的甲种品牌饮水机和D、E两种型号的乙种品牌饮水机,某中学准备从甲、乙两种品牌的饮水机中各选购一种型号的饮水机安装到教室.
⑴ 写出所有的选购方案,如果各种选购方案被选中的可能性相同,那么A型号饮水机被选中的概率是多少?
⑵ 如果该学校计划用1万元人民币购买甲、乙两种品牌的饮水机共24台(价格如表格所示),其中甲种品牌饮水机选为A型号的,请你算算该中学购买到A型号饮水机共多少台?
|
品 牌 |
甲 |
乙 |
|||
|
型 号 |
A |
B |
C |
D |
E |
|
单价(元) |
600 |
400 |
250 |
500 |
200 |
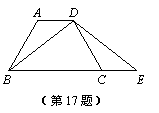
17.(9分)如图,等腰梯形ABCD中,AD∥BC,延长BC到E,使CE=AD.
⑴ 用尺规作图法,过点D作DM⊥BE,垂足为M(不写作法,保留作图痕迹);
⑵判断BM、ME的大小关系,并说明理由.
16.(8分)先化简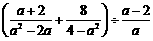 ,然后从
,然后从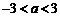 的范围内选取一个你认为合适的整数作为
的范围内选取一个你认为合适的整数作为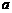 的值代入求值.
的值代入求值.
15.如图,在△ABC中,∠C=90°,AB=10,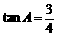 ,经过点C且与边AB相切的动圆与CA、CB分别交于点D、E,则线段DE长度的最小值是__________.
,经过点C且与边AB相切的动圆与CA、CB分别交于点D、E,则线段DE长度的最小值是__________.
14.如图,分别过点Pi(i,0)(i=1、2、…、n)作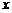 轴的垂线,交
轴的垂线,交 的图象于点Ai,交直线
的图象于点Ai,交直线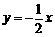 于点Bi.则
于点Bi.则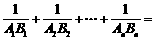 _________.
_________.
13.如图,坐标系的原点为O,点P是第一象限内抛物线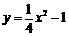 上的任意一点,PA⊥x轴于点A.则
上的任意一点,PA⊥x轴于点A.则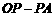 =__________.
=__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com