
题目列表(包括答案和解析)
14、如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为
13cm.
考点:平面展开-最短路径问题.
专题:几何图形问题.
分析:要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.
解答:解:
∵PA=2×(4+2)=12,QA=5
∴PQ=13.
故答案为:13.
点评:本题主要考查两点之间线段最短,以及如何把立体图形转化成平面图形.
13、若等式 (x3-2)0=1成立,则x的取值范围是
x>6,
12、如图,⊙O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是
50°
11、已知A=2x,B是多项式,在计算B+A时,小马虎同学把B+A看成了B÷A,结果得x2+ 12x,则B+A=
2x3+x2+2x
 考点:整式的混合运算.
考点:整式的混合运算.
专题:计算题.
分析:根据乘除法的互逆性首先求出B,然后再计算B+A.
解答:解:∵B÷A=x2+ 12x,
∴B=(x2+ 12x)•2x=2x3+x2.
∴B+A=2x3+x2+2x,
故答案为:2x3+x2+2x,
点评:此题主要考查了整式的乘法,以及整式的加法,题目比较基础,基本计算是考试的重点.
10、 图①是一瓷砖的图案,用这种瓷砖铺设地面,图②铺成了一个2×2的近似正方形,其中完整菱形共有5个;若铺成3×3的近似正方形图案③,其中完整的菱形有13个;铺成 4×4的近似正方形图案④,其中完整的菱形有25个;如此下去,可铺成一个n×n的近似正方形图案.当得到完整的菱形共181个时,n的值为( )D
图①是一瓷砖的图案,用这种瓷砖铺设地面,图②铺成了一个2×2的近似正方形,其中完整菱形共有5个;若铺成3×3的近似正方形图案③,其中完整的菱形有13个;铺成 4×4的近似正方形图案④,其中完整的菱形有25个;如此下去,可铺成一个n×n的近似正方形图案.当得到完整的菱形共181个时,n的值为( )D
A、7 B、8 C、9 D、10
 考点:规律型:图形的变化类.
考点:规律型:图形的变化类.
专题:规律型.
分析:观察图形特点,从中找出数字规律,图①菱形数为,2×12-2×1+1=1,图②为,2×22-2×2+1=5,图③为,2×32-2×3+1=13,图④为,2×42-2×4+1=25,…,据此规律可表示出图n的菱形数,由已知得到关于n的方程,从求出n的值.
解答:解:由已知通过观察得:
图①菱形数为,2×12-2×1+1=1,
图②为,2×22-2×2+1=5,
图③为,2×32-2×3+1=13,
图④为,2×42-2×4+1=25,
…,
所以铺成一个n×n的近似正方形图案的菱形个数为:
2n2-2n+1,
则2n2-2n+1=181,
解得:n=10或n=-9(舍去),
故选:D.
点评:此题考查的知识点是图形数字的变化类问题,解题的关键是先观察分析总结出规律,根据规律列方程求解.
9、关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2,且有x1-x1x2+x2=1-a,则a的值是( )C
A、1 B、-1 C、1或-1 D、2
考点:根与系数的关系;根的判别式.
专题:计算题.
分析:根据根与系数的关系得出x1+x2=- ba,x1x2= ca,整理原式即可得出关于a的方程求出即可.
解答:解:∵关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2,且有x1-x1x2+x2=1-a,
∴x1-x1x2+x2=1-a,
∴x1+x2-x1x2=1-a,
∴ 3a+1a- 2a+2a=1-a,
解得:a=±1,
故选:C.
点评:此题主要考查了根与系数的关系,由x1-x1x2+x2=1-a,得出x1+x2-x1x2=1-a是解决问题的关键.
8、在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )D
A、 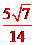 B、
B、 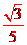 C、
C、 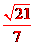 D、
D、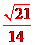
考点:解直角三角形.
专题:几何图形问题.
分析:根据∠A=120°,得出∠DAC=60°,∠ACD=30°,得出AD=1,CD= 3,再根据BC=2 7,利用解直角三角形求出.
解答:解:延长BA做CD⊥BD,
∵∠A=120°,AB=4,AC=2,
∴∠DAC=60°,∠ACD=30°,
∴2AD=AC=2,
∴AD=1,CD= 3,
∴BD=5,
∴BC=2 7,
∴sinB= 327= 2114,
故选:D.
点评:此题主要考查了解直角三角形以及勾股定理的应用,根据题意得出∠DAC=60°,∠ACD=30°是解决问题的关键.
7、
 如图,P为线段AB上一点,AD与BC交干E,∠CPD=∠A=∠B,BC交PD于E,AD交PC于G,则图中相似三角形有( )B
如图,P为线段AB上一点,AD与BC交干E,∠CPD=∠A=∠B,BC交PD于E,AD交PC于G,则图中相似三角形有( )B
A、1对B、2对C、3对D、4对
考点:相似三角形的判定.
专题:证明题.
分析:根据题目提供的相等的角和图形中隐含的相等的角,利用两对应角对应相等的两三角形相似找到相似三角形即可.
解答:解:∵∠CPD=∠A=∠B,
∴△PCE∽△BCP
△APG∽△BFP
故选B.
点评:本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角.
6、对于非零的两个实数a、b,规定a⊗b= 1b-1a.若1⊗(x+1)=1,则x的值为( )D
A、 32 B、 13 C、 12 D、- 12
考点:解分式方程.
专题:新定义.
分析:根据规定运算,将1⊗(x+1)=1转化为分式方程,解分式方程即可.
解答:解:由规定运算,1⊗(x+1)=1可化为, 1x+1-1=1,
即 1x+1=2,解得x=- 12,
故选D.
点评:本题考查了解分式方程的方法:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.
5、有13位同学参加学校组织的才艺表演比赛.已知他们所得的分数互不相同,共设7个获奖名额.某同学知进自己的比赛分数后,要判断自己能否获奖,在下列13名同学成绩的统计量中只需知道一个量,它是( )C
A、众数B、方差C、中位数D、平均数
考点:统计量的选择;中位数.
专题:应用题.
分析:由于比赛设置了7个获奖名额,共有13名选手参加,故应根据中位数的意义分析.
解答:解:因为7位获奖者的分数肯定是17名参赛选手中最高的,
而且13个不同的分数按从小到大排序后,中位数及中位数之后的共有7个数,
故只要知道自己的分数和中位数就可以知道是否获奖了.
故选C.
点评:此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.反映数据集中程度的统计量有平均数、中位数、众数、方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com