
题目列表(包括答案和解析)
20.(本题满分10分)
解:设建筑物CD与EF的延长线交于点G,DG=x米. …………1分
在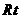 △
△ 中,
中,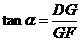 ,即
,即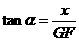 . …………2分
. …………2分
 在
在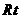 △
△ 中,
中,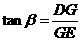 ,即
,即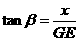 . …………3分
. …………3分
∴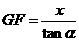 ,
,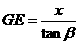 .
.
∴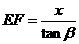
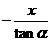 . ………5分
. ………5分
∴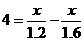 . ………6分
. ………6分
解方程得: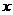 =19.2. ………8分
=19.2. ………8分
∴ 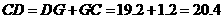 .
.
答:建筑物高为20.4米. ………10分
19.(本题满分8分)
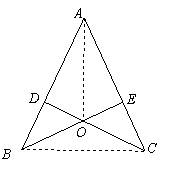 (1)证明:在△ACD与△ABE中,
(1)证明:在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,
∴ △ACD≌△ABE.…………………… 3分
∴ AD=AE. ……………………4分
(2) 互相垂直 ……………………5分
在Rt△ADO与△AEO中,
∵OA=OA,AD=AE,
∴ △ADO≌△AEO. ……………………………………6分
∴ ∠DAO=∠EAO.
即OA是∠BAC的平分线. ………………………………………7分
又∵AB=AC,
∴ OA⊥BC. ………………………………………8分
18.(本题满分8分)
解:(1)20, 8, 0.4, 0.16 -----------------------------4分
(2)57.6 ----------------------------6分
(3)由上表可知达到优秀和良好的共有19+20=39人,
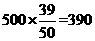 人.
-----------------------------8分
人.
-----------------------------8分
17.(本小题满分7分)
|
|
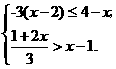
解不等式①,得 x 1
----------2分
1
----------2分
解不等式②,得 x<4.
所以,不等式组的解集为:
1 x<4 ---------------------------4分
x<4 ---------------------------4分
在数轴上表示为:
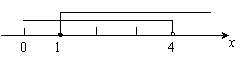
--------------------------6分
9.(-1,-2); 10.3;11.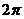 ;12.
;12.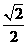 ;13.① ④;14.3; 15.
;13.① ④;14.3; 15.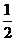 ; 16.
; 16.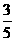 或
或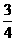 .
.
3.如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.
2.解答题每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数.本答案对每小题只给出一种或两种解法,对考生的其他解法,请参照评分意见进行评分.
1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.
23. (本题满分12分)
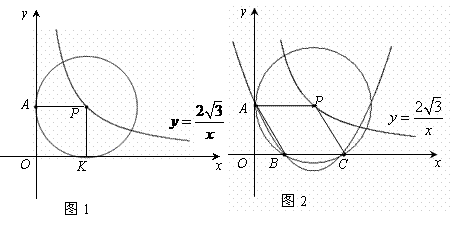
在直角坐标系xoy中,已知点P是反比例函数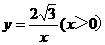 图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的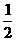 .若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
.若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
德州市二○一一年初中学业考试
数学试题参考解答及评分意见
评卷说明:
22. (本题满分10分)
●观察计算
当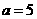 ,
,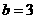 时,
时, 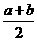 与
与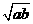 的大小关系是_________________.
的大小关系是_________________.
当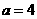 ,
,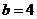 时,
时, 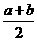 与
与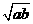 的大小关系是_________________.
的大小关系是_________________.
●探究证明
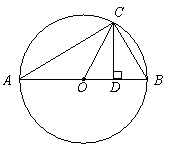 如图所示,
如图所示,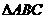 为圆O的内接三角形,
为圆O的内接三角形,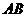 为直径,过C作
为直径,过C作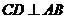 于D,设
于D,设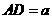 ,BD=b.
,BD=b.
(1)分别用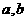 表示线段OC,CD;
表示线段OC,CD;
(2)探求OC与CD表达式之间存在的关系
(用含a,b的式子表示).
●归纳结论
根据上面的观察计算、探究证明,你能得出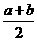 与
与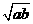 的大小关系是:_________________________.
的大小关系是:_________________________.
●实践应用
要制作面积为1平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com