
题目列表(包括答案和解析)
9. 按图1的方法把圆锥的侧面展开,得到图2,其半径OA=3,圆心角∠AOB=120°,则AB的长为(■).
按图1的方法把圆锥的侧面展开,得到图2,其半径OA=3,圆心角∠AOB=120°,则AB的长为(■).
(A)π (B)2π (C)3π (D)4π
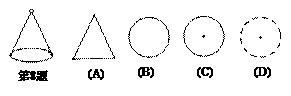
8.一个圆锥体按如图所示摆放,它的主视图是(■).
7.下列计算正确的是(■).
(A)3a-a=3 (B)2a·a3=a6 (C)(3a3)2=2a6 (D)2a÷a=2
6.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向远移时,圆形阴影的大小的变化情况是(■).
(A)越来越小 (B)越来越大 (C)大小不变 (D)不能确定
5.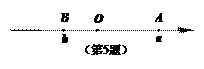 如图,数轴上A,B两点分别对应实数a,b,则下列结论正确的是( ■).
如图,数轴上A,B两点分别对应实数a,b,则下列结论正确的是( ■).
(A)a<b (B)a=b (C)a>b (D)ab>0
4.我市大约有34万中小学生参加了“廉政文化进校园”教育活动,将数据34万用科学记数法表示,正确的是(■ ).
(A)0.34×105 (B)3.4×105 (C)34×105 (D)340×105
3.要调查城区九年级8000名学生了解禁毒知识的情况,下列调查方式最合适的是(■).
(A)在某校九年级选取50名女生 (B)在某校九年级选取50名男生
(C)在某校九年级选取50名学生 (D)在城区8000名九年级学生中随机选取50名学生
2.如果用+0.02克表示一只乒乓球质量超出标准质量0.02克,那么一只乒乓球质量低于标准质量0.02克记作(■).
(A)+0.02克 (B)-0.02克 (C) 0克 (D)+0.04克
1.如图,用数学的眼光欣赏这个蝴蝶图案,它的一种数学美体现在蝴蝶图案的(■).
(A)轴对称性 (B)用字母表示数 (C)随机性 (D)数形结合
24、如图甲,分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA 所在直线为x轴、y轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在x轴上),抛物线y= 14x2+bx+c经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
(1)求B点坐标;
(2)求证:ME是⊙P的切线;
(3)设直线AC与抛物线对称轴交于N,Q点是此轴称轴上不与N点重合的一动点,
①求△ACQ周长的最小值;
②若FQ=t,S△ACQ=S,直接写出S与t之间的函数关系式.

考点:二次函数综合题.
分析:(1)如图甲,连接PE、PB,设PC=n,由正方形CDEF的面积为1,可得CD=CF=1,根据圆和正方形的对称性知:OP=PC=n,由PB=PE,根据勾股定理即可求得n的值,继而求得B的坐标;
(2)由(1)知A(0,2),C(2,0),即可求得抛物线的解析式,然后求得FM的长,则可得△PEF∽△EMF,则可证得∠PEM=90°,即ME是⊙P的切线;
(3)①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=3于Q,连AQ,则有AQ=A′Q,△ACQ周长的最小值为AC+A′C的长,利用勾股定理即可求得△ACQ周长的最小值;
②分别当Q点在F点上方时,当Q点在线段FN上时,当Q点在N点下方时去分析即可求得答案.
解答:解:(1)如图甲,连接PE、PB,设PC=n,
∵正方形CDEF的面积为1,
∴CD=CF=1,
根据圆和正方形的对称性知:OP=PC=n,
∴BC=2PC=2n,
∵而PB=PE,
∴PB2=BC2+PC2=4n2+n2=5n2,PE2=PF2+EF2=(n+1)2+1,
∴5n2=(n+1)2+1,
解得:n=1或n=- 12(舍去),
∴BC=OC=2,
∴B点坐标为(2,2);
(2)如图甲,由(1)知A(0,2),C(2,0),
∵A,C在抛物线上,
\∴ {c=214×4+2b+c=0,
解得: {c=2b=-32,
∴抛物线的解析式为:y= 14x2- 32x+2= 14(x-3)2- 14,
∴抛物线的对称轴为x=3,即EF所在直线,
∵C与G关于直线x=3对称,
∴CF=FG=1,
∴MF= 12FG= 12,
在Rt△PEF与Rt△EMF中,
∠EFM=∠EFP,
∵ FMEF=121=12, EFPF=12,
∴ FMEF=EFPF,
∴△PEF∽△EMF,
∴∴∠EPF=∠FEM,
∴∠PEM=∠PEF+∠FEM=∠PEF+∠EPF=90°,
∴ME是⊙P的切线;

(3)①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=3于Q,连AQ,
则有AQ=A′Q,
∴△ACQ周长的最小值为AC+A′C的长,
∵A与A′关于直线x=3对称,
∴A(0,2),A′(6,2),
∴A′C=(6-2)2+22=2 5,而AC=22+22=2 2,
∴△ACQ周长的最小值为2 2+2 5;
②当Q点在F点上方时,S=t+1,
当Q点在线段FN上时,S=1-t,
当Q点在N点下方时,S=t-1.
点评:此题考查了待定系数法求二次函数的解析式,圆的性质,相似三角形的判定与性质以及勾股定理等知识.此题综合性很强,题目难度较大,解题的关键是方程思想、分类讨论与数形结合思想的应用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com