
题目列表(包括答案和解析)
12、(2011•泰安)若点A的坐标为(6,3)O为坐标原点,将OA绕点O按顺时针方向旋转90°得到OA′,则点A′的坐标是( )
A、(3,﹣6) B、(﹣3,6)
C、(﹣3,﹣6) D、(3,6)
考点:坐标与图形变化-旋转。
专题:作图题。
分析:正确作出A旋转以后的A′点,即可确定坐标.
解答:解:由图知A点的坐标为(6,3),
根据旋转中心O,旋转方向顺时针,旋转角度90°,画图,
点A′的坐标是(3,﹣6).
故选A.

点评:本题考查了图形的旋转,抓住旋转的三要素:旋转中心O,旋转方向顺时针,旋转角度90°,通过画图得A′.
11、(2011•泰安)某班为奖励在校运会上取得较好成绩的运动员,花了400元钱购买甲.乙两种奖品共30件,其中甲种奖品每件16元,乙种奖品每件12元,求甲乙两种各买多少件?该问题中,若设购买甲种奖品x件,乙种奖品y件,则列方程正确的是( )
A、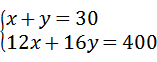 B、
B、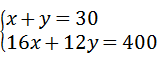
C、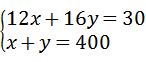 D、
D、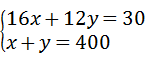
考点:由实际问题抽象出二元一次方程组。
专题:应用题。
分析:根据甲乙两种奖品共30件,可找到等量关系列出一个方程,在根据甲乙两种奖品的总价格找到一个等量关系列出一个方程,将两个方程组成一个二元一次方程组.
解答:解:若设购买甲种奖品x件,乙种奖品y件,
甲.乙两种奖品共30件,所以x+y=30
因为甲种奖品每件16元,乙种奖品每件12元,所以16x+12y=400
由上可得方程组: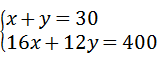
故选B.
点评:本题考查根据实际问题抽象出方程组:根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.
10、(2011•泰安)如图,⊙O的弦AB垂直平分半径OC,若AB=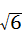 ,则⊙O的半径为( )
,则⊙O的半径为( )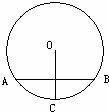
A、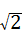 B、
B、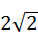
C、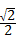 D、
D、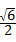
考点:垂径定理;勾股定理。
专题:探究型。
分析:连接OA,设⊙O的半径为r,由于AB垂直平分半径OC,AB=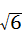 则AD=
则AD=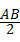 =
=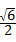 ,OD=
,OD=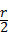 ,再利用勾股定理即可得出结论.
,再利用勾股定理即可得出结论.
解答:解:连接OA,设⊙O的半径为r,
∵AB垂直平分半径OC,AB=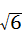 ,
,
∴AD=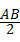 =
=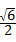 ,OD=
,OD=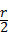 ,
,
在Rt△AOD中,
OA2=OD2+AD2,即r2=(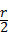 )2+(
)2+(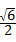 )2,
)2,
解得r=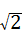 .
.
故选A.

点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
9、(2011•泰安)某校篮球班21名同学的身高如下表
|
身高cm |
180 |
186 |
188 |
192 |
208 |
|
人数(个) |
4 |
6 |
5 |
4 |
2 |
则该校蓝球班21名同学身高的众数和中位数分别是(单位:cm)( )
A、186,186 B、186,187
C、186,188 D、208,188
考点:众数;中位数。
分析:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据.
解答:解:众数是:188cm;
中位数是:188cm.
故选C.
点评:本题为统计题,考查极差、众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
8、(2011•泰安)如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为( )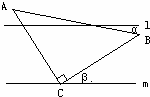
A、25° B、30°
C、20° D、35°
考点:平行线的性质;对顶角、邻补角;三角形的外角性质。
专题:计算题。
分析:根据平角的定义求出∠ACR,根据平行线的性质得出∠FDC=∠ACR=70°,求出∠AFD,即可得到答案.
解答:解:
∵∠β=20°,∠ACB=90°,
∴∠ACR=180°﹣90°﹣20°=70°,
∵l∥m,
∠FDC=∠ACR=70°,
∴∠AFD=∠FDC﹣∠A=70°﹣45°=25°,
∴∠a=∠AFD=25°,
故选A.
点评:本题主要考查对平行线的性质,三角形的外角性质,对顶角、邻补角等知识点的理解和掌握,求出∠AFD的度数是解此题的关键.
7、(2011•泰安)下列运算正确的是( )
A、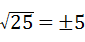 B、
B、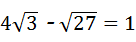
C、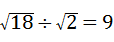 D、
D、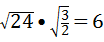
考点:二次根式的混合运算。
专题:计算题。
分析:根据二次根式运算的法则,分别计算得出各答案的值,即可得出正确答案.
解答:解:A.∵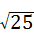 =5,∴故此选项错误;
=5,∴故此选项错误;
B.∵4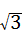 ﹣
﹣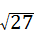 =4
=4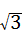 ﹣3
﹣3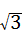 =
=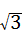 ,∴故此选项错误;
,∴故此选项错误;
C.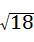 ÷
÷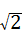 =
=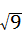 =3,∴故此选项错误;
=3,∴故此选项错误;
D.∵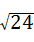 •
•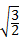 =
=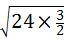 =6,∴故此选项正确.
=6,∴故此选项正确.
故选:D.
点评:此题主要考查了二次根式的混合运算,熟练化简二次根式后,在加减的过程中,有同类二次根式的要合并;相乘的时候,被开方数简单的直接让被开方数相乘,再化简;较大的也可先化简,再相乘,灵活对待.
6、(2011•泰安)下列几何体:
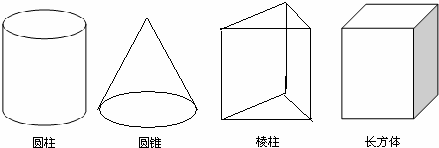
其中,左视图是平行四边形的有( )
A、4个 B、3个
C、2个 D、1个
考点:简单几何体的三视图。
分析:左视图是从几何体的左面看所得到的图形.
解答:解:圆柱的左视图是长方形,长方形是一个特殊的平行四边形;
圆锥的左视图是三角形;
棱柱的左视图是长方形,长方形是一个特殊的平行四边形;
长方体的左视图是长方形,长方形是一个特殊的平行四边形;
故左视图是平行四边形的有3个,
故选:B,
点评:此题主要考查了几何体的三视图,解决此类图的关键是由立体图形得到三视图,以及考查学生空间想象能力.
5、(2011•泰安)下列等式不成立的是( )
A、m2﹣16=(m﹣4)(m+4) B、m2+4m=m(m+4)
C、m2﹣8m+16=(m﹣4)2 D、m2+3m+9=(m+3)2
考点:提公因式法与公式法的综合运用。
专题:因式分解。
分析:由平方差公式,提公因式以及完全平方公式分解因式的知识求解即可求得答案.
解答:解:A、m2﹣16=(m﹣4)(m+4),故本选项正确;
B、m2+4m=m(m+4),故本选项正确;
C、m2﹣8m+16=(m﹣4)2,故本选项正确;
D、m2+3m+9≠(m+3)2,故本选项错误.
故选D.
点评:此题考查了因式分解的知识.注意因式分解的步骤:先提公因式,再用公式法分解,注意分解要彻底.
4、(2011•泰安)第六次全国人口普查公布的数据表明,登记的全国人靠数量约为1 340 000 000人.这个数据用科学记数法表示为( )
A、134×107人 B、13.4×108人
C、1.34×109人 D、1.34×1010人
考点:科学记数法-表示较大的数。
分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答:解:1 340 000 000=1.34×109人.
故选C.
点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3、(2011•泰安)下列图形:

其中是中心对称图形的个数为( )
A、1 B、2
C、3 D、4
考点:中心对称图形。
专题:图表型。
分析:根据轴对称图形与中心对称图形的概念求解.
解答:解:一图是轴对称图形,二图是中心对称图形,三图是轴对称图形,四图即是中心对称图形,也是周对称图形;
所以,中心对称图形的个数为2.
故选B.
点评:本题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com