
题目列表(包括答案和解析)
15、(2011•南充)先化简,再求值: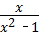 (
(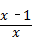 ﹣2),其中x=2.
﹣2),其中x=2.
考点:分式的化简求值。
专题:计算题。
分析:先通分,计算括号里的,再利用乘法进行约分计算,最后把x的值代入计算即可.
解答:解:原式=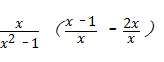 =
=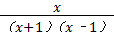 ×
×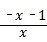 =
=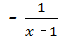 ,
,
当x=2时,原式=﹣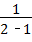 =﹣1.
=﹣1.
点评:本题考查了分式的化简求值.解题的关键是注意对分式的分子、分母因式分解.
14、(2011•南充)过反比例函数y=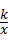 (k≠0)图象上一点A,分别作x轴,y轴的垂线,垂足分别为B,C,如果△ABC的面积为3.则k的值为 6或﹣6 .
(k≠0)图象上一点A,分别作x轴,y轴的垂线,垂足分别为B,C,如果△ABC的面积为3.则k的值为 6或﹣6 .
考点:反比例函数系数k的几何意义。
专题:计算题。
分析:根据△ABC的面积为反比例函数比例系数的绝对值的一半可得k的值.
解答:解:∵△ABC的面积为反比例函数比例系数的绝对值的一半,
∴ |k|=3,
|k|=3,
解得k=6或﹣6,
故答案为6或﹣6.
点评:考查反比例函数系数k的几何意义;得到△ABC的面积与反比例函数比例系数的关系是解决本题的关键.
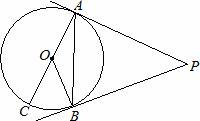
13、(2011•南充)如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠BAC=25°,则∠P= 50 度.
考点:切线的性质;多边形内角与外角。
专题:几何图形问题。
分析:首先利用切线长定理可得PA=PB,再根据∠OBA=∠BAC=25°,得出∠ABP的度数,再根据三角形内角和求出.
解答:解:∵PA,PB是⊙O是切线,A,B为切点,
∴PA=PB,∠OBP=90°,
∵OA=OB,
∴∠OBA=∠BAC=25°,
∴∠ABP=90°﹣25°=65°,
∵PA=PB,
∴∠BAP=∠ABP=65°,
∴∠P=180°﹣65°﹣65°=50°,
故答案为:50°.
点评:此题主要考查了切线的性质以及三角形内角和定理,得出∠ABP是解决问题的关键.
12、(2011•南充)某灯具厂从1万件同批次产品中随机抽取了100件进行质检,发现其中有5件不合格,估计该厂这一万件产品中不合格品约为 500 件.
考点:用样本估计总体。
分析:首先可以求出样本的不合格率,然后利用样本估计总体的思想即可求出这一万件产品中不合格品约为多少件.
解答:解:∵某灯具厂从1万件同批次产品中随机抽取了100件进行质检,发现其中有5件不合格,
∴不合格率为:5÷100=5%,
∴估计该厂这一万件产品中不合格品为10000×5%=500件.
故答案为:500.
点评:此题主要考查了利用样本估计总体的思想,解题时首先求出样本的不合格率,然后利用样本估计总体的思想即可解决问题.
11、(2011•南充)计算(π﹣3)0= 1 .
考点:零指数幂。
专题:计算题。
分析:根据零指数幂的性质即可得出答案.
解答:解:(π﹣3)0=1,
故答案为1.
点评:本题主要考查了零指数幂的性质,比较简单.
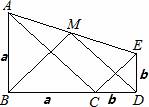
10、(2011•南充)如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=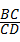 ;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )
;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )

A、1个 B、2个
C、3个 D、4个
考点:锐角三角函数的定义;等腰三角形的判定与性质;等腰直角三角形;梯形中位线定理。
专题:证明题。
分析:①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知,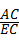 =
=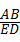 =
=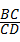 ;然后由直角三角形中的正切函数,得tan∠AEC=
;然后由直角三角形中的正切函数,得tan∠AEC=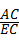 ,再由等量代换求得tan∠AEC=
,再由等量代换求得tan∠AEC=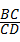 ;
;
②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab(a=b时取等号)解答;
③、④通过作辅助线MN,构建直角梯形的中位线,根据梯形的中位线定理及等腰直角三角形的判定定理解答.
解答:解:∵△ABC和△CDE均为等腰直角三角形,
∴AB=BC,CD=DE,
∴∠BAC=∠BCA=∠DCE=∠DEC=45°,
∴∠ACE=90°;
∵△ABC∽△CDE
∴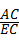 =
=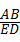 =
=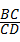
①∴tan∠AEC=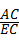 ,
,
∴tan∠AEC=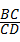 ;故本选项正确;
;故本选项正确;
②∵S△ABC= a2,S△CDE=
a2,S△CDE= b2,S梯形ABDE=
b2,S梯形ABDE= (a+b)2,
(a+b)2,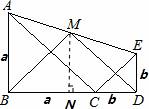
∴S△ACE=S梯形ABDE﹣S△ABC﹣S△CDE=ab,
S△ABC+S△CDE= (a2+b2)≥ab(a=b时取等号),
(a2+b2)≥ab(a=b时取等号),
∴S△ABC+S△CDE≥S△ACE;故本选项正确;
④过点M作MN垂直于BD,垂足为N.
∵点M是AE的中点,
则MN为梯形中位线,
∴N为中点,
∴△BMD为等腰三角形,
∴BM=DM;故本选项正确;
③又MN= (AB+ED)=
(AB+ED)= (BC+CD),
(BC+CD),
∴∠BMD=90°,
即BM⊥DM;故本选项正确.
故选D.
点评:本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点.在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
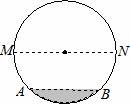
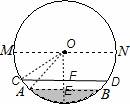
9、(2011•南充)在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )
A、6分米 B、8分米
C、10分米 D、12分米
考点:垂径定理的应用。
分析:如图,油面AB上升1分米得到油面CD,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,由垂径定理,得AE= AB=3,CF=
AB=3,CF= CD=4,设OE=x,则OF=x﹣1,在Rt△OAE中,OA2=AE2+OE2,在Rt△OCF中,OC2=CF2+OF2,由OA=OC,列方程求x即可求半径OA,得出直径MN.
CD=4,设OE=x,则OF=x﹣1,在Rt△OAE中,OA2=AE2+OE2,在Rt△OCF中,OC2=CF2+OF2,由OA=OC,列方程求x即可求半径OA,得出直径MN.
解答:解:如图,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,
由垂径定理,得AE= AB=3,CF=
AB=3,CF= CD=4,
CD=4,
设OE=x,则OF=x﹣1,
在Rt△OAE中,OA2=AE2+OE2,
在Rt△OCF中,OC2=CF2+OF2,
∵OA=OC,
∴32+x2=42+(x﹣1)2,
解得x=4,
∴半径OA=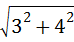 =5,
=5,
∴直径MN=2OA=10分米.
故选C.
点评:本题考查了垂径定理的运用.关键是利用垂径定理得出两个直角三角形,根据勾股定理表示半径的平方,根据半径相等列方程求解.
8、(2008•温州)若分式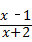 的值为零,则x的值是( )
的值为零,则x的值是( )
A、0 B、1
C、﹣1 D、﹣2
考点:分式的值为零的条件。
专题:计算题。
分析:分式的值是0的条件是:分子为0,分母不为0,则可得x﹣1=0且x+2≠0,从而解决问题.
解答:解:∵x﹣1=0且x+2≠0,
∴x=1.
故选B.
点评:分式是0的条件中特别需要注意的是分母不能是0,这是经常考查的知识点.
7、(2011•南充)小明乘车从南充到成都,行车的平均速度v(km/h)和行车时间t(h)之间的函数图象是( )
A、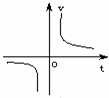 B、
B、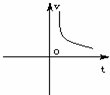
C、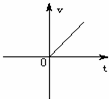 D、
D、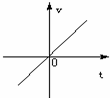
考点:反比例函数的应用;反比例函数的图象。
专题:数形结合。
分析:根据时间t、速度v和路程s之间的关系,在路程不变的条件下,得v=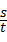 ,则v是t的反比例函数,且t>0.
,则v是t的反比例函数,且t>0.
解答:解:∵v=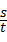 (t>0),
(t>0),
∴v是t的反比例函数,
故选B.
点评:本题是一道反比例函数的实际应用题,注:在路程不变的条件下,v是t的反比例函数.
6、(2011•南充)方程(x+1)(x﹣2)=x+1的解是( )
A、2 B、3
C、﹣1,2 D、﹣1,3
考点:解一元二次方程-因式分解法。
专题:计算题。
分析:先移项得到(x+1)(x﹣2)﹣(x+1)=0,然后利用提公因式因式分解,再化为两个一元一次方程,解方程即可.
解答:解:(x+1)(x﹣2)﹣(x+1)=0,
∴(x+1)(x﹣2﹣1)=0,即(x+1)(x﹣3)=0,
∴x+1=0,或x﹣3=0,
∴x1=﹣1,x2=3.
故选D.
点评:本题考查了运用因式分解法解一元二次方程的方法:利用因式分解把一个一元二次方程化为两个一元一次方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com