
题目列表(包括答案和解析)
22.解:(1)作BF⊥y轴于F.
∵A(0,10),B(8,4)
∴FB=8,FA=6,
|
 (2)由图2可知,点P从点A运动到点B用了10s
(2)由图2可知,点P从点A运动到点B用了10s

|
∴P、Q两点的运动速度均为每秒一个单位长度.
(3)解法1:作PG⊥y轴于G,则PG∥BF.
∴△AGP∽△AFB
∴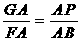 ,即
,即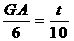 .
.
∴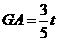 .
.
∴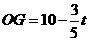 .
.
又∵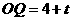
∴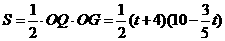
即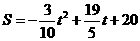
∵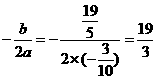 ,且
,且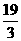 在0≤t≤10内,
在0≤t≤10内,
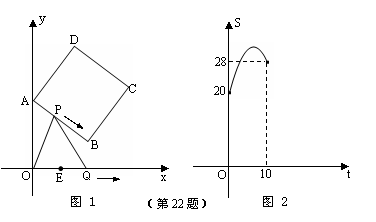
∴当 时,S有最大值.
时,S有最大值.
此时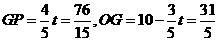 ,
,
∴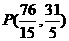
解法2:由图2,可设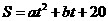 ,
,
∵抛物线过(10,28)∴可再取一个点,当t=5时,计算得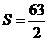 ,
,
∴抛物线过( ),代入解析式,可求得a,b.
),代入解析式,可求得a,b.
(4)这样的点P有2个.
海淀区九年级第二学期期末练习-数 学
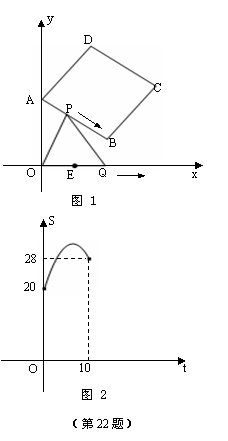
22.如图1,正方形ABCD的顶点A,B的坐标分别为(0,10),(8,4),顶点C,D在第一象限.点P从点A出发,沿正方形按逆时针方向运动,同时,点Q从点E(4,0)出发,沿x轴正方向以相同速度运动.当点P到达点C时,P,Q两点同时停止运动.设运动时间为t(s).
(1)求正方形ABCD的边长.
(2)当点P在AB边上运动时,△OPQ的面积S(平方单位)与时间t(s)之间的函数图像为抛物线的一部分(如图2所示),求P,Q两点的运动速度.
(3)求(2)中面积S(平方单位)与时间t(s)的函数解析式及面积S取最大值时点P的坐标.
(4)若点P,Q保持(2)中的速度不变,则点P沿着AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小.当点P沿着这两边运动时,能使∠OPQ=90°吗?若能,直接写出这样的点P的个数;若不能,直接写不能.
28.(本小题满分12分)
解:(1)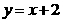 1分
1分
(2) 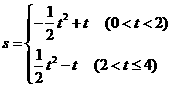 5分
5分
(3)一共四个点,(0,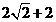 ),(0,0),(0,
),(0,0),(0,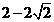 ),(0,-2)。
),(0,-2)。
(4)当P点运动时,线段EG的长度不发生改变,为定值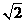 。
。
当0<t<2时,过G作GH⊥y轴,垂足为H.
由AP=t,可得AE= 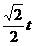 .
.
由相似可得GH=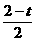 ,
,
所以GC=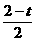
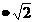 .
.
于是,GE=AC-AE-GC=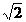 .
.
即GE的长度不变.
当2<t ≤ 4时,同理可证.
综合得:当P点运动时,线段EG的长度不发生改变,为定值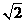 12分
12分
2011年广东省初中毕业生学业考试
数 学 试 卷
(6月押题卷)
27.(本小题满分10分)
解: (1)y=-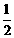 x2+4, M(
x2+4, M(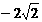 ,0),N(
,0),N(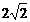 ,0)
(3分)
,0)
(3分)
① yC'=-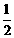 x2+6
(5分),
x2+6
(5分),
yD'=-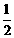 (x+2)2+4
(7分)
(x+2)2+4
(7分)
②G(1-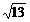 ,-3+
,-3+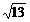 )
(10分)
)
(10分)
28.(本题满分12分)如图,二次函数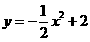 与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
 (1)求直线AC的解析式;
(1)求直线AC的解析式;
(2)设△PQC的面积为S,求S关于t的函数解析式;
(3)在y轴上找一点M,使△MAC和△MBC都是等
腰三角形。直接写出所有满足条件的M点的坐标;
(4)过点P作PE⊥AC,垂足为E,当P点运动时,
线段EG的长度是否发生改变,请说明理由。
27.
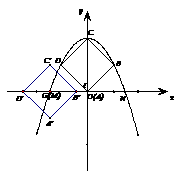
(本题满分10分) 如图1,把一个边长为2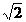 的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边).
的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边).
(1)求抛物线c1的解析式及点M、N的坐标;
(2)如图2,另一个边长为2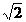 的正方形
的正方形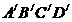 的中心G在点M上,
的中心G在点M上,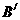 、
、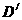 在x轴的负半轴上(
在x轴的负半轴上(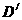 在
在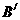 的左边),点
的左边),点 在第三象限,当点G沿着抛物线c1从点M移到点N,正方形
在第三象限,当点G沿着抛物线c1从点M移到点N,正方形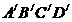 随之移动,移动中
随之移动,移动中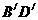 始终与x轴平行.
始终与x轴平行.
①直接写出点C’、D’移动路线形成的抛物线C(C’)、C(D’)的函数关系式;
②如图3,当正方形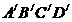 第一次移动到与正方形ABCD有一边在同一直线上时,
第一次移动到与正方形ABCD有一边在同一直线上时,
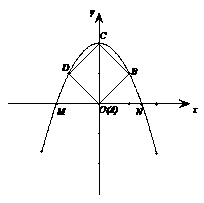 求点G的坐标.
求点G的坐标.
|
|
|

23、(10分)解(1)设此抛物线的解析式为: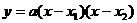
∵抛物线与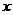 轴交于A(1,0)、B(
轴交于A(1,0)、B(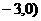 两点,
两点,
∴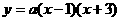
又∵抛物线与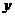 轴交于点C(0,3)
轴交于点C(0,3)
∴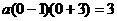 ,
,
∴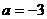
∴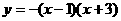
即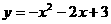 ……………3分
……………3分
用其他解法参照给分
(2)∵点A(1,0),点C(0,3)
∴OA=1,OC=3,
∵DC⊥AC,OC⊥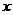 轴
轴
∴△QOC∽△COA
∴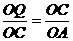 ,即
,即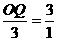
∴OQ=9,……………………4分
又∵点Q在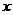 轴的负半轴上,∴Q(
轴的负半轴上,∴Q(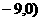
设直线DC的解析式为: ,则
,则
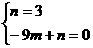 解之得:
解之得: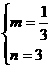
∴直线DC的解析式为: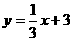 ……………………5分
……………………5分
∵点D是抛物线与直线DC的交点,
∴ 解之得:
解之得: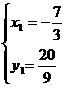
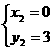 (不合题意,应舍去)
(不合题意,应舍去)
∴点D(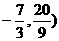 ……………………6分
……………………6分
用其他解法参照给分
(3)如图,点M为直线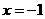 上一点,连结AM,PC,PA
上一点,连结AM,PC,PA
设点M(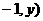 ,直线
,直线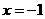 与
与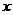 轴交于点E,∴AE=2
轴交于点E,∴AE=2
∵抛物线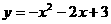 的顶点为P,对称轴为
的顶点为P,对称轴为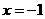
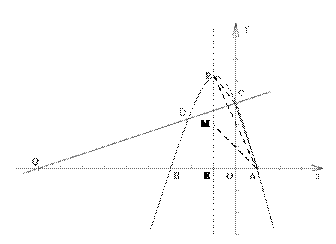 ∴P(
∴P(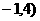
∴PE=4
则PM=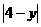
∵S四边形AEPC=S四边形OEPC+S△AOC
=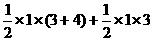
=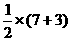
=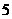 ……………………7分
……………………7分
又∵S四边形AEPC= S△AEP+S△ACP
S△AEP=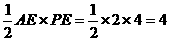
∴+S△ACP=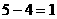 ……………………8分
……………………8分
∵S△MAP=2S△ACP
∴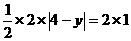
∴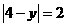
∴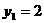 ,
,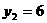 ……………………9分
……………………9分
故抛物线的对称轴上存在点M使S△MAP=2S△ACP
点M(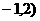 或
或 ……………………10分
……………………10分
用其他解法参照给分
二O一一年常州市中考模拟试卷数学试卷
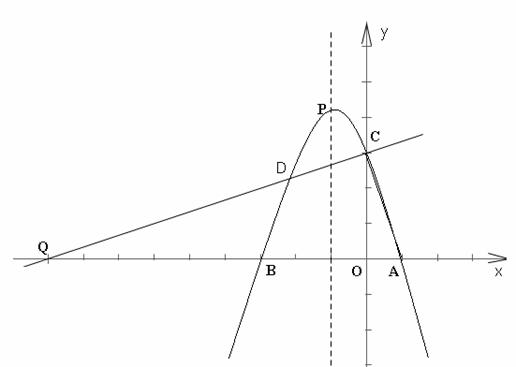
23、(达州市2011年)(10分)如图,已知抛物线与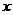 轴交于A(1,0),B(
轴交于A(1,0),B(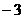 ,0)两点,与
,0)两点,与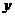 轴交于点C(0,3),抛物线的顶点为P,连结AC.
轴交于点C(0,3),抛物线的顶点为P,连结AC.
(1)求此抛物线的解析式;
(2)在抛物线上找一点D,使得DC与AC垂直,且直线DC与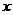 轴交于点Q,求点D的坐标;
轴交于点Q,求点D的坐标;
(3)抛物线对称轴上是否存在一点M,使得S△MAP=2S△ACP,若存在,求出M点坐标;若不存在,请说明理由.
26.(本题满分12分)
 解: (1)由
解: (1)由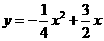 得
得 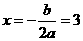 …………1分
…………1分
∴D(3,0)…………2分
(2)方法一:
如图1, 设平移后的抛物线的解析式为
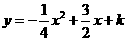 …………3分
…………3分
则C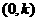 OC=
OC=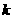
令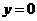 即
即 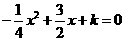
得 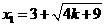
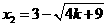 …………4分
…………4分
∴A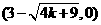 ,B
,B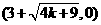
∴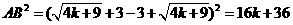 ………5分
………5分
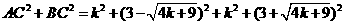
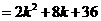 ……………………6分
……………………6分
∵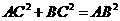
即: 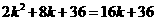
得 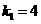
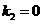 (舍去) ……………7分
(舍去) ……………7分
∴抛物线的解析式为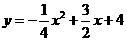 ……………8分
……………8分
方法二:
∵ 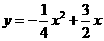 ∴顶点坐标
∴顶点坐标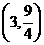
设抛物线向上平移h个单位,则得到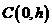 ,顶点坐标
,顶点坐标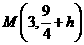 …………3分
…………3分
∴平移后的抛物线: 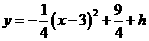 ……………………4分
……………………4分
当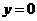 时,
时, 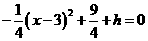 , 得
, 得 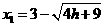

∴ A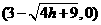 B
B ……………………5分
……………………5分
∵∠ACB=90° ∴△AOC∽△COB
∴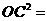 OA·OB……………………6分
OA·OB……………………6分
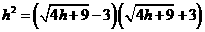 得
得 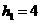 ,
, …………7分
…………7分
∴平移后的抛物线: 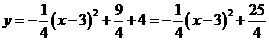 …………8分
…………8分
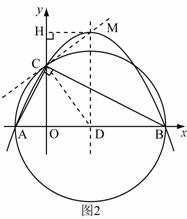
(3)方法一:
如图2, 由抛物线的解析式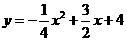 可得
可得
A(-2 ,0),B(8,0) ,C(4,0)
,M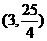 …………9分
…………9分
 过C、M作直线,连结CD,过M作MH垂直y轴于H,
过C、M作直线,连结CD,过M作MH垂直y轴于H,
则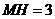
∴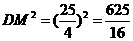
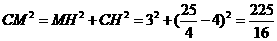
在Rt△COD中,CD=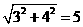 =AD
=AD
∴点C在⊙D上 …………………10分
∵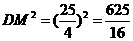
 ……11分
……11分
∴
∴△CDM是直角三角形,∴CD⊥CM
∴直线CM与⊙D相切 …………12分
方法二:
如图3, 由抛物线的解析式可得
A(-2 ,0),B(8,0) ,C(4,0)
,M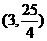 …………9分
…………9分
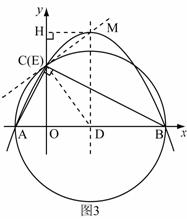 作直线CM,过D作DE⊥CM于E, 过M作MH垂直y轴于H,则
作直线CM,过D作DE⊥CM于E, 过M作MH垂直y轴于H,则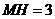 ,
, 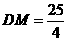 , 由勾股定理得
, 由勾股定理得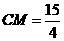
∵DM∥OC
∴∠MCH=∠EMD
∴Rt△CMH∽Rt△DME …………10分
∴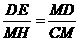 得
得 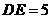 …………11分
…………11分
由(2)知 ∴⊙D的半径为5
∴⊙D的半径为5
∴直线CM与⊙D相切 …………12分
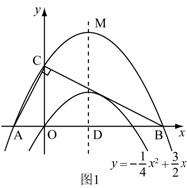
26.(2011年桂林市)(本题满分12分)已知二次函数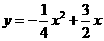 的图象如图.
的图象如图.
(1)求它的对称轴与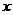 轴交点D的坐标;
轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与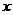 轴,
轴,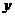 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com