
题目列表(包括答案和解析)
23.(本题满分8分)某区共有甲、乙、丙三所高中,所有高二学生参加了一次数学测试.老师们对其中的一道题进行了分析,把每个学生的解答情况归结为下列四类情况之一:A--概念错误;B--计算错误;C--解答基本正确,但不完整;D--解答完全正确.各校出现这四类情况的人数分别占本校高二学生数的百分比如下表所示.
|
|
A |
B |
C |
 D D |
|
甲校(%) |
2.75 |
16.25 |
60.75 |
20.25 |
|
乙校(%) |
3.75 |
22.50 |
41.25 |
32.50 |
|
丙校(%) |
12.50 |
6.25 |
22.50 |
58.75 |
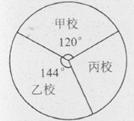
已知甲校高二有400名学生,这三所学校高二学生人数的扇形
统计图如图.
根据以上信息,解答下列问题:
(1)求全区高二学生总数;
(2)求全区解答完全正确的学生数占全区高二学生总数的百分比m(精确到0.01%);
(3)请你对表中三校的数据进行对比分析,给丙校高二数学老师提一个值得关注的问题,并 说明理由.
[答案]解: (1) ∵从扇形统计图可知甲校高二学生达1200即全区高二学生总数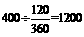 人.
人.
(2) 由(1) 知全区高二学生总数为1200人
则乙校高二学生数为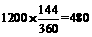 人,
人,
丙校高二学生数为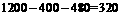 人
人
∴全区解答完全正确的学生数为
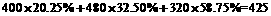 人
人
∴全区解答完全正确的学生数占全区高二学生总数的百分比m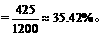
(3) 从表中三校的数据进行对比分析, 丙校高二学生概念错误的比例达12.50%,在三所学校中是最高的, 因此丙校高二数学老师应加强基本概念的教学.
[考点]扇形统计图, 频数的计算, 统计图表的分析, 有理数的近似值。
 [分析]已知甲校高二学生数和占全区高二学生总数的比例很易求出全区高二学生总数. 求全区解答完全正确的学生数占全区高二学生总数的百分比只要求出全区解答完全正确的学生数即可求得. 对表中三校的数据进行对比分析找出丙校高二学生的薄弱环节, 提出丙校高二数学老师值得关注的问题.
[分析]已知甲校高二学生数和占全区高二学生总数的比例很易求出全区高二学生总数. 求全区解答完全正确的学生数占全区高二学生总数的百分比只要求出全区解答完全正确的学生数即可求得. 对表中三校的数据进行对比分析找出丙校高二学生的薄弱环节, 提出丙校高二数学老师值得关注的问题.
22.(本题满分7分)一不透明的袋子中装有4个球,它们除了上面分别标有的号码l、2、3、4不同外,其余均相同.将小球搅匀,并从袋中任意取出一球后放回;再将小球搅匀,并从袋中再任意取出一球.求第二次取出球的号码比第一次的大的概率.(请用“画树状图”或“列表”的方法给出分析过程,并写出结果)
[答案]解:用列表法
|
|
1 |
2 |
3 |
4 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
(1,4) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
(2,4) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
(3,4) |
|
4 |
(4,1) |
(4,2) |
(4,3) |
(4,4) |
共有16种情况, 其中第二次取出球的号码比第一次大的有6种情况(1,2), (1,3), (1,4), (2,3), (2,4), (3,4).∴第二次取出球的号码比第一次的大的概率是
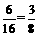
[考点]概率。
[分析]列举出所有情况,看第二次取出球的号码比第一次的大的有多少即可求得第二次取出球的号码比第一次的大的概率.
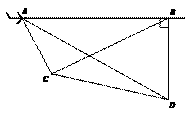
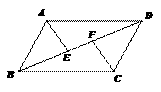
21. (本题满分8分)如图,在 ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.
(本题满分8分)如图,在 ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.
求证:BE=DF.
[答案]证明:∵ 四边形ABCD是平行四边形
∴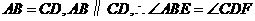
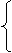 ∴在
∴在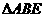 和
和 中
中 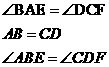
∴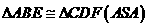 ∴
∴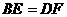
[考点]平行四边形的性质, 平行线的性质, 全等三角形的判定和性质。
[分析]要证明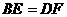 , 只要求证
, 只要求证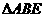 和
和 全等, 利用平行四边形对边平行且相等和平行线内错角相等的性质可得
全等, 利用平行四边形对边平行且相等和平行线内错角相等的性质可得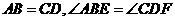 ,又由巳知
,又由巳知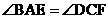 ,根据全等三角形的判定定理
,根据全等三角形的判定定理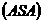 得证.
得证.
20.(本题满分8分)
(1)解方程:x2+4x-2=0;
[答案]解: 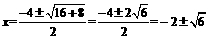
[考点]-元二次方程求根公式。
[分析]利用-元二次方程求根公式,直接得出结果.
(2)解不等式组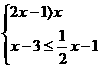
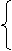
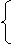 [答案]解: 由
[答案]解: 由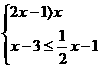

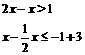

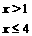
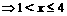
[考点]-元一次不等式组。
[分析]利用-元一次不等式组求解方法,直接得出结果.
19.(本题满分8分)计算:
(1)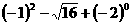
[答案]解: 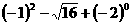 =1-4+1=-2
=1-4+1=-2
[考点]负数的偶次方,算术平方根和零次幂。
[分析]利用负数的偶次方,算术平方根和零次幂的定义,直接得出结果.
(2)a(a-3)+(2-a)(2+a)
[答案]解: 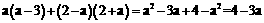
[考点]单项式乘多项式,平方差公式。
[分析]利用单项式乘多项式,平方差公式,直接得出结果.
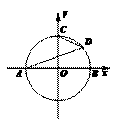
18.如图,以原点O为圆心的圆交X轴于A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=20°,则∠OCD= ▲ °.
[答案]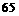
[考点]圆周角。
[分析]利用同(等)弧所对圆周角相等的结论,直接得出结果: 设⊙O交y轴的负半轴于点E, 连接AE ,则圆周角 ∠OCD =圆周角∠DAE =∠DAB+∠BAE ,易知∠BAE所对弧的圆心角为900. 故∠BAE=450. 从而∠OCD=200+450=650
17.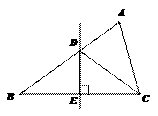 如图,在△ABC中,AB=5cm,AC=3cm,BC的垂直平分线分别交AB、BC于D、E,则 △ACD的周长为 ▲ cm.
如图,在△ABC中,AB=5cm,AC=3cm,BC的垂直平分线分别交AB、BC于D、E,则 △ACD的周长为 ▲ cm.
[答案]8
[考点]垂直平分线。
[分析]利用线段垂直平分线性质,直接得出结果: △ACD的周长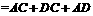
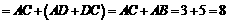
 [点评]主要考查线段垂直平分线性质,要求熟练掌握: 线段垂直平分线上任意一点,到线段两端点的距离相等.
[点评]主要考查线段垂直平分线性质,要求熟练掌握: 线段垂直平分线上任意一点,到线段两端点的距离相等.
16.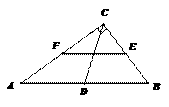 如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5cm,则EF= ▲ cm.
如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5cm,则EF= ▲ cm.
[答案]5
[考点]三角形中位线定理和直角三角形性质。
[分析]利用三角形中位线定理和直角三角形性质,直接得出结果
15.正五边形的每一个内角都等于 ▲ °.
[答案]108
[考点]n边形的内角和。
[分析]利用n边形的内角和定理,直接得出正五边形的内角和是540,再除以5即得.
14.请写出一个大于1且小于2的无理数: ▲ .
[答案]
[考点]无理数。
[分析]利用无理数的定义,直接得出结果
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com