
题目列表(包括答案和解析)
10. (2011山东枣庄,22,8分)某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
解:(1)设组建中型图书角x个,则组建小型图书角为(30-x)个.由题意,得
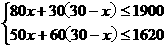 ……………………………………2分
……………………………………2分
解这个不等式组,得18≤x≤20.
由于x只能取整数,∴x的取值是18,19,20.
当x=18时,30-x=12;当x=19时,30-x=11;当x=20时,30-x=10.
故有三种组建方案:方案一,中型图书角18个,小型图书角12个;方案二,中型图书
角19个,小型图书角11个;方案三,中型图书角20个,小型图书角10个. …5分
(2)方案一的费用是:860×18+570×12=22320(元);
方案二的费用是:860×19+570×11=22610(元);
方案三的费用是:860×20+570×10=22900(元).
故方案一费用最低,最低费用是22320元. ……………………………………8分
9. (2011贵州安顺,24,10分)某班到毕业时共结余班费1800元,班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件T恤或一本影集作为纪念品.已知每件T恤比每本影集贵9元,用200元恰好可以买到2件T恤和5本影集.
⑴求每件T恤和每本影集的价格分别为多少元?
⑵有几种购买T恤和影集的方案?
[答案](1)设T恤和影集的价格分别为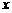 元和
元和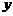 元.则
元.则
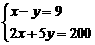
解得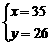
答:T恤和影集的价格分别为35元和26元.
(2)设购买T恤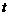 件,则购买影集 (50-
件,则购买影集 (50-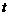 )
本,则
)
本,则
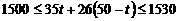
解得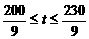 ,∵
,∵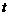 为正整数,∴
为正整数,∴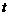 = 23,24,25,
= 23,24,25,
即有三种方案.第一种方案:购T恤23件,影集27本;
第二种方案:购T恤24件,影集26本;
第三种方案:购T恤25件,影集25本.
8. (2011湖北鄂州,20,8分)今年我省干旱灾情严重,甲地急需要抗旱用水15万吨,乙地13万吨.现有A、B两水库各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.
⑴设从A水库调往甲地的水量为x万吨,完成下表


|
甲 |
乙 |
总计 |
||||||
|
A |
x |
|
14 |
||||||
|
B |
|
|
14 |
||||||
|
总计 |
15 |
13 |
28 |
⑵请设计一个调运方案,使水的调运量尽可能小.(调运量=调运水的重量×调运的距离,单位:万吨•千米)
[答案]⑴(从左至右,从上至下)14-x 15-x x-1
⑵y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275
解不等式1≤x≤14
所以x=1时y取得最小值
ymin=1280
7. (2011重庆市潼南,25,10分)潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两
种植户种植的两类蔬菜的种植面积与总收入如下表:
|
种植户 |
种植A类蔬菜面积 (单位:亩) |
种植B类蔬菜面积 (单位:亩) |
总收入 (单位:元) |
|
甲 |
3 |
1 |
12500 |
|
乙 |
2 |
3 |
16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
⑴ 求A、B两类蔬菜每亩平均收入各是多少元?
⑵ 某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.
[答案]解:(1)设A、B两类蔬菜每亩平均收入分别是x元,y元.
由题意得: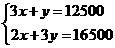 ----------------3分
----------------3分
解得: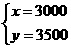
答:A、B两类蔬菜每亩平均收入分别是3000元,3500元.----5分
(2)设用来种植A类蔬菜的面积a亩,则用来种植B类蔬菜的面积为(20-a)亩.
由题意得: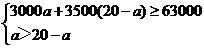 ----------7分
----------7分
解得:10<a≤14.
∵a取整数为:11、12、13、14. ----------------------------8分
∴租地方案为:
|
类别 |
种植面积 单位:(亩) |
|||
|
A |
11 |
12 |
13 |
14 |
|
B |
9 |
8 |
7 |
6 |
---------------------------10分
6. (2011内蒙古乌兰察布,23,10分),某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个,摆放在迎宾大道两侧.已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆.
(l)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
[答案]⑴设搭建A种园艺造型x个,则搭建B种园艺造型(50-x)个.
根据题意得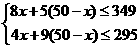 解得
解得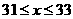 ,
,
所以共有三种方案①A :31 B:19
②A :32 B:18
③A :33 B:17
⑵由于搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,所以搭配同样多的园艺造型A种比B种成本低,则应该搭配A种33个,B种17个.
成本:33×200+17×360=12720(元)
说明:也可列出成本和搭配A种造型数量x之间的函数关系,用函数的性质求解;或直接算出三种方案的成本进行比较也可.
5. (2011湖北黄石,23,8分)今年,号称“千湖之省”的湖北正遭受大旱,为提高学生环保意识,节约用水,某校数学教师编造了一道应用题:
|
月用水量(吨) |
单价(元/吨) |
|
不大于10吨部分 |
1.5 |
|
大于10吨不大于m吨部分 (20≤m≤50) |
2 |
|
大于m吨部分 |
3 |
为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
(1) 若某用户六月份用水量为18吨,求其应缴纳的水费;
(2) 记该户六月份用水量为x吨,缴纳水费y元,试列出y关于x的函数式;
(3) 若该用户六月份用水量为40吨,缴纳消费y元的取值范围为70≤y≤90,试求m的取值范围。
各位同学,请你也认真做一做,相信聪明的你一定会顺利完成。
[答案]解:(1)10×1.5+(18-10)×2=31
(2)①当x≤10时
y=1.5x
②当10< x≤m时
y=10×1.5+(x-10)×2=2x-5
③当x>m时
y=10×1.5+(m-10)×2+(x-m)×3
(3) ①当40吨恰好是第一档与第二档时
2×40-5=75
符合题意
②当40吨恰好是第一档、第二档与第三档时
70≤10×1.5+(m-10)×2+(40-m)×3≤90
70≤-m+115≤90
25 ≤m≤45
4.(2011湖北黄冈,20,8分)今年我省干旱灾情严重,甲地急需要抗旱用水15万吨,乙地13万吨.现有A、B两水库各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.
⑴设从A水库调往甲地的水量为x万吨,完成下表


|
甲 |
乙 |
总计 |
||||||
|
A |
x |
|
14 |
||||||
|
B |
|
|
14 |
||||||
|
总计 |
15 |
13 |
28 |
⑵请设计一个调运方案,使水的调运量尽可能小.(调运量=调运水的重量×调运的距离,单位:万吨•千米)
[答案]⑴(从左至右,从上至下)14-x 15-x x-1
⑵y=50x+(14-x)30+60(15-x)+(x-1)45=5x+1275
解不等式1≤x≤14
所以x=1时y取得最小值
ymin=1280
3. (2011四川凉山州,24,9分)我州鼓苦荞茶、青花椒、野生蘑菇,为了让这些珍宝走出大山,走向世界,州政府决定组织21辆汽车装运这三种土特产共120吨,参加全国农产品博览会。现有A型、B型、C型三种汽车可供选择。已知每种型号汽车可同时装运2种土特产,且每辆车必须装满。根据下表信息,解答问题。
|
|
 |
苦荞茶 |
青花椒 |
野生蘑菇 |
|
|
每 辆 汽 车 运 载 量 |
(吨) |
A型 |
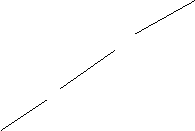 2 2 |
2 |
|
|
B型 |
4 |
|
2 |
||
|
C型 |
|
1 |
6 |
|
车型 |
A |
B |
C |
|
每辆车运费(元) |
1500 |
1800 |
2000 |
(1)
设A型汽车安排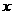 辆,B 型汽车安排
辆,B 型汽车安排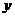 辆,求
辆,求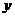 与
与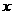 之间的函数关系式。
之间的函数关系式。
(2) 如果三种型号的汽车都不少于4辆,车辆安排有几种方案?并写出每种方案。
(3) 为节约运费,应采用(2)中哪种方案?并求出最少运费。
[答案]
解:⑴ 法① 根据题意得
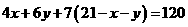
化简得: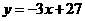
法② 根据题意得
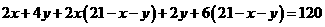
化简得: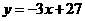
⑵由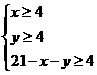 得
得 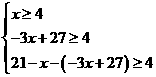
解得 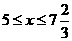 。
。
∵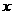 为正整数,∴
为正整数,∴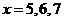
故车辆安排有三种方案,即:
方案一: 型车
型车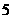 辆,
辆,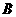 型车
型车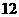 辆,
辆,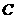 型车
型车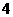 辆
辆
方案二: 型车
型车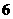 辆,
辆,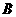 型车
型车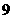 辆,
辆,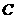 型车
型车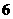 辆
辆
方案三: 型车
型车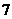 辆,
辆,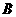 型车
型车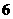 辆,
辆,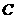 型车
型车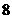 辆
辆
⑶设总运费为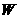 元,则
元,则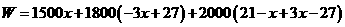
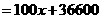
∵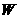 随
随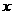 的增大而增大,且
的增大而增大,且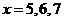
∴当 时,
时,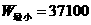 元
元
答:为节约运费,应采用 ⑵中方案一,最少运费为37100元。
2. (2011重庆綦江,25,10分)为了保护环境,某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%,实际运行中发现,每台甲型设备每月能处理污水200吨,每台乙型设备每月能处理污水160吨,且每年用于每台甲型设备的各种维护费和电费为1万元,每年用于每台乙型设备的各种维护费和电费为1.5万元.今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两型设备共8台用于二期工程的污水处理,预算本次购买资金不超过84万元,预计二期工程完成后每月将产生不少于1300吨污水.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元?
(2)请你求出用于二期工程的污水处理设备的所有购买方案;
(3)若两种设备的使用年限都为10年,请你说明在(2)的所有方案中,哪种购买方案的总费用最少?(总费用=设备购买费+各种维护费和电费)
[答案]:25. 解:(1)设一台甲型设备的价格为x万元,由题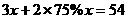 ,解得x=12,∵ 12×75%=9 ,∴ 一台甲型设备的价格为12万元,一台乙型设备的价格是9万元
,解得x=12,∵ 12×75%=9 ,∴ 一台甲型设备的价格为12万元,一台乙型设备的价格是9万元
(2)设二期工程中,购买甲型设备a台,由题意有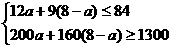 ,解得:
,解得: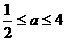
由题意a为正整数,∴a=1,2,3,4 ∴所有购买方案有四种,分别为
方案一:甲型1台,乙型7台; 方案二:甲型2台,乙型6台
方案三:甲型3台,乙型5台; 方案四:甲型4台,乙型4台
(3)设二期工程10年用于治理污水的总费用为W万元
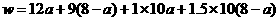 化简得:
化简得: 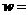 -2a+192,
-2a+192,
∵W随a的增大而减少 ∴当a=4时, W最小(逐一验算也可)
∴按方案四甲型购买4台,乙型购买4台的总费用最少.
1. ( 2011重庆江津, 26,12分) 在“五个重庆”建设中,为了提高市民的宜居环境,某区规划修建一个文化广场(平面图形如图所示),其中四边形ABCD是矩形,分别以AB、BC、CD、DA边为直径向外作半圆,若整个广场的周长为628米,高矩形的边长AB=y米,BC=x米.(注:取π=3.14)
(1)试用含x的代数式表示y;
(2)现计划在矩形ABCD区域上种植花草和铺设鹅卵石等,平均每平方米造价为428元,在四个半圆的区域上种植草坪及铺设花岗岩,平均每平方米造价为400元;
①设该工程的总造价为W元,求W关于x的函数关系式;
②若该工程政府投入1千万元,问能否完成该工程的建设任务?若能,请列出设计方案,若不能,请说明理由?
③若该工程在政府投入1千万元的基础上,又增加企业募捐资金64·82万元,但要求矩形的边BC的长不超过AB长的三分之二,且建设广场恰好用完所有资金,问:能还完成该工程的建设任务?若能,请列出所有可能的设计方案,若不能,请说明理由·
 [答案](1) 由题意得
[答案](1) 由题意得 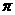 y+
y+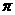 x=6·28
x=6·28
∵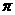 =3.14 ∴3.14y+3.14x=628.
=3.14 ∴3.14y+3.14x=628.
∴x+y=200.则 y=200-x;
(2)
①w=428xy+400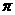 (
(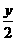 )2+400
)2+400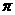 (
(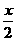 )2
)2
=428x(200-x)+400×3.14×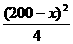 +400×3.14×
+400×3.14×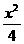
=200x2-40000x+12560000;
②仅靠政府投入的1千万不能完成该工程的建设任务,其理由如下:
由①知 w=200(x-100)2+1.056×107>107, 所以不能;
③由题意得 x≤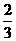 y, 即x≤
y, 即x≤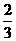 (200-x) 解之得 x≤80
(200-x) 解之得 x≤80
∴0≤x≤80.
又根据题意得 w=200(x-100)2+1.056×107=107+6.482×105
整理得 (x-100)2=441 解之得 x1=79, x2=121 (不合题意舍去)
∴只能取 x=79, 则y=200-79=121
所以设计的方案是: AB长为121米,BC长为79米,再分别以各边为直径向外作半圆·
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com