
题目列表(包括答案和解析)
3. (2011湖北黄石,24,9分)已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,C为O2上一点(不与A,B,O1重合),直线CB与⊙O1交于另一点D。
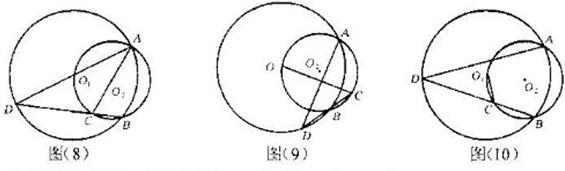
(1)如图(8),若AC是⊙O2的直径,求证:AC=CD
(2)如图(9),若C是⊙O1外一点,求证:O1C⊥AD
(3)如图(10),若C是⊙O1内的一点,判断(2)中的结论是否成立。
[答案](1)连接C O1,AB
∵AC是⊙O2的直径
∴AB⊥BD,AD⊥C O1
∴AD经过点O1
∵AO1=DO1
∴AC=CD
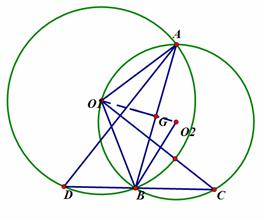
(2)连接O1 O2,AO1
∵O1 O2⊥AB
∴∠AO1O2+∠AG O1
∵∠O1AB=∠C
又∵∠D= ∠AO1B=∠AO1O2
∠AO1B=∠AO1O2
∴∠C+∠D=900
∴O1C⊥AD
(3)成立
2. (2011江苏南京,26,8分)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
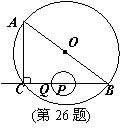

[答案]解:⑴直线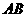 与⊙P相切.
与⊙P相切.
如图,过点P作PD⊥AB, 垂足为D.
在Rt△ABC中,∠ACB=90°,∵AC=6cm,BC=8cm,
∴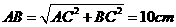 .∵P为BC的中点,∴PB=4cm.
.∵P为BC的中点,∴PB=4cm.
∵∠PDB=∠ACB=90°,∠PBD=∠ABC.∴△PBD∽△ABC.
∴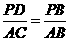 ,即
,即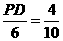 ,∴PD
=2.4(cm) .
,∴PD
=2.4(cm) .
当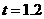 时,
时,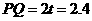 (cm)
(cm)
∴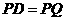 ,即圆心
,即圆心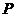 到直线
到直线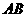 的距离等于⊙P的半径.
的距离等于⊙P的半径.
∴直线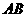 与⊙P相切.
与⊙P相切.
⑵ ∠ACB=90°,∴AB为△ABC的外切圆的直径.∴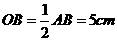 .
.
连接OP.∵P为BC的中点,∴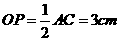 .
.
∵点P在⊙O内部,∴⊙P与⊙O只能内切.
∴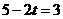 或
或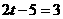 ,∴
,∴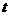 =1或4.
=1或4.
∴⊙P与⊙O相切时,t的值为1或4.
1. (2011江西,20,8分)有一种用来画圆的工具板(如图所示),工具板长21cm,上面依次排列着大小不等的五个圆(孔),共中最大圆的直径为3cm,其余圆的直径从左到右依次递减0.2cm.最大圆的左侧距工具板左侧边缘1.5cm,最小圆的右侧距工具板右侧边缘1.5cm,相邻两圆的间距d均相等。
⑴直接写出其余四个圆的直径长;
⑵求相邻两圆的间距。
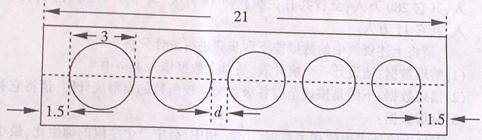
[答案](1)其余四个圆的直径长分别为2.8cm,2.6cm,2.4cm,2.2cm;
(2)因为工具板长21cm,左、右侧边缘1.5cm,
所以的五个圆(孔)及相邻两圆的间距之和为21-3=18(cm).
d=[18-(3+2.8+2.6+2.4+2.2)]÷4=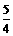 (cm).
(cm).
12.
11.
10.
9.
8.
7.
6. (2011山东枣庄,17,4分)如图,小圆的圆心在原点,半径为3,大圆的圆心坐标为(a,0),半径为5.如果两圆内含,那么a的取值范围是________.
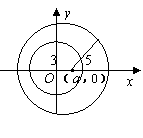

[答案]-2<a<2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com