
题目列表(包括答案和解析)
3. (2011山东威海,24,11分)如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
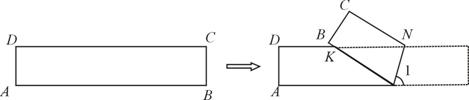
(1)若∠1=70°,求∠MNK的度数.
(2)△MNK的面积能否小于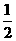 ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.

(备用图)
[答案] 解:∵ABCD是矩形,
 ∴AM∥DN,
∴AM∥DN,
∴∠KNM=∠1.
∵∠KMN=∠1,
∴∠KNM=∠KMN.
∵∠1=70°,
∴∠KNM=∠KMN=70°.
∴∠MNK=40°.
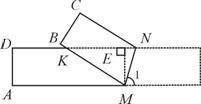
(2)不能.
过M点作ME⊥DN,垂足为点E,则ME=AD=1,
由(1)知∠KNM=∠KMN.
∴MK=NK.
又MK≥ME,
∴NK≥1.
∴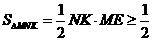 .
.
∴△MNK的面积最小值为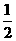 ,不可能小于
,不可能小于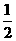 .
.
(3)分两种情况:
情况一:将矩形纸片对折,使点B与点D重合,此时点K也与点D重合.
设MK=MD=x,则AM=5-x,由勾股定理,得
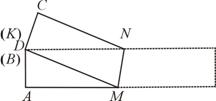
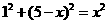 ,
,
解得,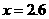 .
.
即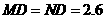 .
.
∴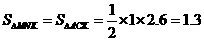 .
(情况一)
.
(情况一)
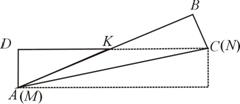 情况二:将矩形纸片沿对角线AC对折,此时折痕为AC.
情况二:将矩形纸片沿对角线AC对折,此时折痕为AC.
设MK=AK= CK=x,则DK=5-x,同理可得
即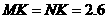 .
.
∴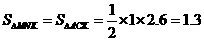 .
.
∴△MNK的面积最大值为1.3. (情况二)
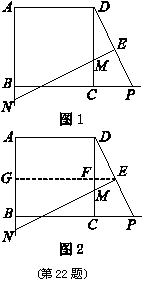
2. (2011山东济宁,22,8分)数学课上,李老师出示了这样一道题目:如图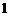 ,正方形
,正方形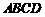 的边长为
的边长为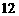 ,
, 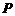 为边
为边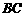 延长线上的一点,
延长线上的一点,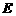 为
为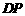 的中点,
的中点,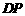 的垂直平分线交边
的垂直平分线交边 于
于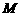 ,交边
,交边 的延长线于
的延长线于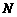 .当
.当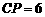 时,
时, 与
与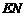 的比值是多少?
的比值是多少?
经过思考,小明展示了一种正确的解题思路:过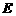 作直线平行于
作直线平行于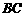 交
交 ,
, 分别于
分别于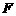 ,
,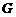 ,如图
,如图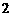 ,则可得:
,则可得: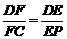 ,因为
,因为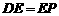 ,所以
,所以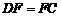 .可求出
.可求出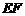 和
和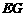 的值,进而可求得
的值,进而可求得 与
与 的比值.
的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了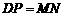 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.

(1)解:过 作直线平行于
作直线平行于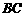 交
交 ,
, 分别于点
分别于点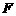 ,
,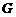 ,
,
则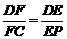 ,
,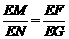 ,
,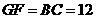 .
.
∵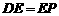 ,∴
,∴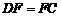 .······· 2分
.······· 2分
∴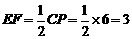 ,
,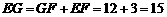 .
.
∴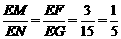 . ··················· 4分
. ··················· 4分
(2)证明:作 ∥
∥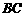 交
交 于点
于点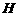 ,················ 5分
,················ 5分
则 ,
,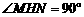 .
.
∵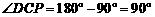 ,
,
∴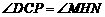 .
.
∵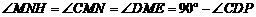 ,
,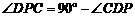 ,
,
∴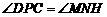 .∴
.∴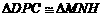 .··········· 7分
.··········· 7分
∴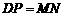 .······················· 8分
.······················· 8分
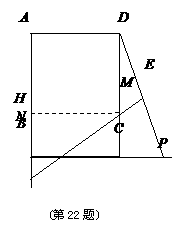

1. (2011四川宜宾,22,7分)如图,飞机沿水平方向(A,B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行距离(因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个求距离MN的方案,要求:
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.

[答案]解:此题为开放题,答案不惟一,只要方案设计合理,可参照给分
⑴如图,测出飞机在A处对山顶的俯角为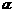 ,测出飞机在B处对山顶的俯角为
,测出飞机在B处对山顶的俯角为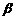 ,测出AB的距离为d,连接AM,BM.
,测出AB的距离为d,连接AM,BM.
⑵第一步,在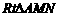 中,
中,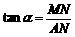 ∴
∴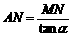
第二步,在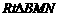 中,
中,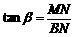 ∴
∴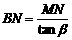
其中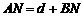 ,解得
,解得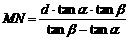 .
.

18.
17. (2011湖北荆州,24,12分)(本题满分12分)如图甲,分别以两个彼此相信的正方形OABC与CDEF的边OC、OA所在直线不x轴、y轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在x轴上),抛物线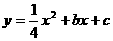 经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
(1)求B点的坐标;
(2)求证:ME是⊙P的切线;
(3)设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,①求△ACQ周长的最小值;②若FQ=t,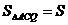 ,直接写出s与t之间的函数关系式.
,直接写出s与t之间的函数关系式.
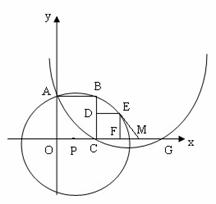
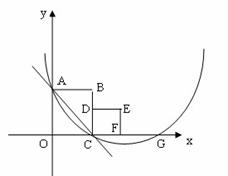
图甲 图乙
[答案]解:(1)如图甲,连接PE、PB,设PC=n
∵正方形CDEF面积为1∴CD=CF=1
根据圆和正方形的对称性知OP=PC=n
∴BC=2PC=2n 而PB=PE,PB2=BC2+PC2=4n2+n2=5n2
又PE2=PF2+EF2=(n+1)2+1
∴5n2=(n+1)2+1
解得n1=1,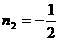 (舍去)
(舍去)
∴BC=OC=2
∴B点坐标为(2,2)
(2)如图甲,由(1)知A(0,2),C(2,0)
∵A,C在抛物线上
∴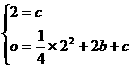 ,解之得:
,解之得: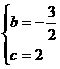
∴抛物线的解析式为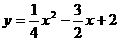 ?
?
∴抛物线的对称轴为x=3,即EF所在直线
∵C与G关于直线x=3对称,∴CF=FG=1
∴MF=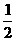 FG=
FG=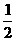
在Rt△PEF与Rt△EMF中
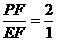 ,
,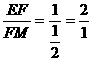
∴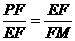 ,而∠PFE=∠FEM=90°
,而∠PFE=∠FEM=90°
∴△PEF∽△EMF
∴∠EPF=∠FEM
∴∠PEM=∠PEF+∠FEM=∠PEF+∠EPF=90°
∴ME与⊙P相切
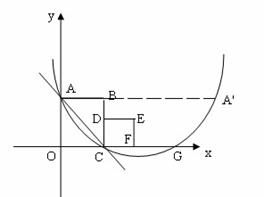
(3)①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=3于Q,连AQ
则有AQ=A′Q,△ACQ周长的最小值为(AC+A′C)的长
∵A与A′关于直线x=3对称
∴A(0,2),A′(6,2)
∴A′C=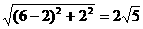 ,
,
而AC=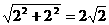
∴△ACQ周长的最小值为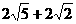
②当Q点在F点上方时,S=t+1
当Q点在线段FN上时,S=1-t
当Q点在N点下方时,S=t-1.
图乙
16. (2011湖南湘潭市,26,10分)(本题满分10分)
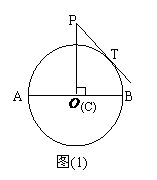
已知,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.
⑴ 如图⑴,当C点运动到O点时,求PT的长;
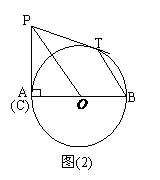
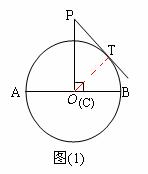
⑵ 如图⑵,当C点运动到A点时,连结PO、BT,求证:PO∥BT;
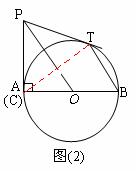
⑶ 如图⑶,设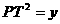 ,
,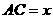 ,求
,求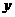 与
与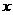 的函数关系式及
的函数关系式及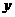 的最小值.
的最小值.


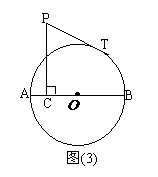

[答案]解:(1)连接OT,
当C点运动到O点时,∵PT为⊙O的切线,∴OT⊥PT,
∴在Rt△PTO中,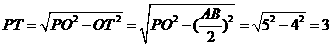 .
.
(2)连接AT,
当C点运动到A点时,∵PC⊥AB,∴PA是⊙O的切线.
∵PT为⊙O的切线,∴PA=PT、PO平分∠APT,∴PO⊥AT.
∵AB是⊙O的直径,∴∠ATB是直角,即BT⊥AT,∴PO∥BT.
⑶连接OP、OT。∵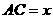 ,∴
,∴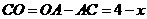 .
.
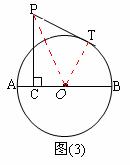
∵在Rt△PCO中,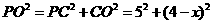
在Rt△POT中,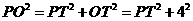 ,
,
∴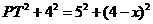 ,即
,即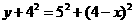 .
.
∴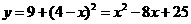 .
.
当x=4时,y最小其值为9.
∴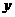 与
与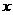 的函数关系式为
的函数关系式为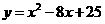 ,
, 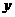 的最小值是9.
的最小值是9.
15.
(2011山东枣庄,25,10分)如图,在平面直角坐标系 中,把抛物线
中,把抛物线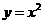 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线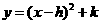 .所得抛物线与
.所得抛物线与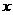 轴交于
轴交于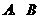 两点(点
两点(点 在点
在点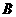 的左边),与
的左边),与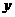 轴交于点
轴交于点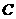 ,顶点为
,顶点为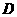 .
.
(1)写出 的值;
的值;
(2)判断 的形状,并说明理由;
的形状,并说明理由;
(3)在线段 上是否存在点
上是否存在点 ,使
,使 ∽
∽ ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
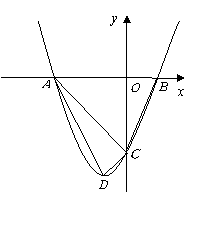

解:(1)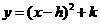 的顶点坐标为D(-1,-4),
的顶点坐标为D(-1,-4),
∴ 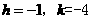 . ……………………………………………………………………2分
. ……………………………………………………………………2分
(2)由(1)得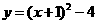 .
.
当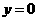 时,
时,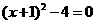 .
解之,得
.
解之,得 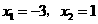 .
.
∴ 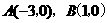 .
.
又当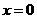 时,
时,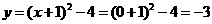 ,
,
∴C点坐标为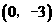 .……………………………………………………………………4分
.……………………………………………………………………4分
又抛物线顶点坐标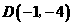 ,作抛物线的对称轴
,作抛物线的对称轴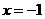 交
交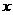 轴于点E,
轴于点E, 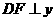 轴于点
轴于点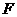 .易知
.易知
在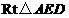 中,
中,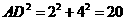 ;
;
在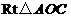 中,
中,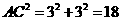 ;
;
在 中,
中,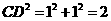 ;
;
∴ 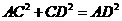 .
.
∴ △ACD是直角三角形. ……………………………………………………………6分
(3)存在.作OM∥BC交AC于M,M点即为所求点.
由(2)知, 为等腰直角三角形,
为等腰直角三角形,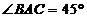 ,
,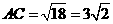 .
.
由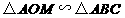 ,得
,得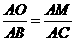 .
.
即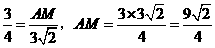 . ……………………………………………………8分
. ……………………………………………………8分
过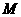 点作
点作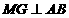 于点
于点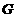 ,则
,则
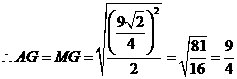 ,
,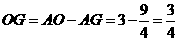 .
.
又点M在第三象限,所以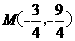 . …………………………………………………10分
. …………………………………………………10分


14. (2011广东湛江28,14分)如图,抛物线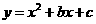 的顶点为
的顶点为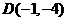 ,与
,与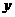 轴相交点
轴相交点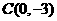 ,与
,与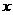 轴交于
轴交于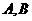 两点(点A在点B的左边).
两点(点A在点B的左边).
(1)求抛物线的解析式;
(2)连接AC,CD,AD,试证明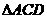 为直角三角形;
为直角三角形;
(3)若点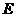 在抛物线的对称轴上,抛物线上是否存在点F,使以A,B,E,F四点为顶点的四边形为平行四边形?若存在,求出满足条件的点F的坐标;若不存在,请说明理由.
在抛物线的对称轴上,抛物线上是否存在点F,使以A,B,E,F四点为顶点的四边形为平行四边形?若存在,求出满足条件的点F的坐标;若不存在,请说明理由.

[答案](1)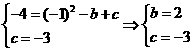 ,所以抛物线的解析式为
,所以抛物线的解析式为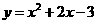 ;
;
(2)因为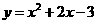 ,可得
,可得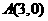 ,
,
所以有
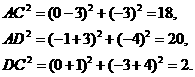
所以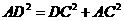 ,所以
,所以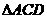 为直角三角形;
为直角三角形;
(3)可知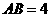 ,假设存在这样的点F,设
,假设存在这样的点F,设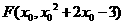 ,所以
,所以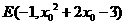 ,
,
要使以A,B,E,F四点为顶点的四边形为平行四边形,只需要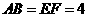 ,即
,即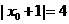 ,所以
,所以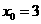 或
或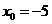 ,因此点F的坐标为
,因此点F的坐标为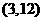 或
或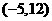 。
。
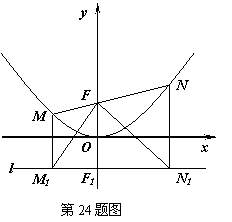
13. (2011湖北鄂州,24,14分)如图所示,过点F(0,1)的直线y=kx+b与抛物线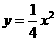 交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
⑴求b的值.
⑵求x1•x2的值
⑶分别过M、N作直线l:y=-1的垂线,垂足分别是M1、N1,判断△M1FN1的形状,并证明你的结论.
⑷对于过点F的任意直线MN,是否存在一条定直线m,使m与以MN为直径的圆相切.如果有,请法度出这条直线m的解析式;如果没有,请说明理由.

[答案]解:⑴b=1
⑵显然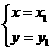 和
和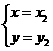 是方程组
是方程组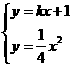 的两组解,解方程组消元得
的两组解,解方程组消元得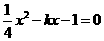 ,依据“根与系数关系”得
,依据“根与系数关系”得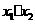 =-4
=-4


⑶△M1FN1是直角三角形是直角三角形,理由如下:
由题知M1的横坐标为x1,N1的横坐标为x2,设M1N1交y轴于F1,则F1M1•F1N1=-x1•x2=4,而FF1=2,所以F1M1•F1N1=F1F2,另有∠M1F1F=∠FF1N1=90°,易证Rt△M1FF1∽Rt△N1FF1,得∠M1FF1=∠FN1F1,故∠M1FN1=∠M1FF1+∠F1FN1=∠FN1F1+∠F1FN1=90°,所以△M1FN1是直角三角形.
⑷存在,该直线为y=-1.理由如下:
直线y=-1即为直线M1N1.
如图,设N点横坐标为m,则N点纵坐标为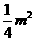 ,计算知NN1=
,计算知NN1=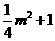 , NF=
, NF=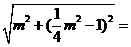
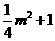 ,得NN1=NF
,得NN1=NF
同理MM1=MF.
那么MN=MM1+NN1,作梯形MM1N1N的中位线PQ,由中位线性质知PQ=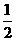 (MM1+NN1)=
(MM1+NN1)=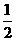 MN,即圆心到直线y=-1的距离等于圆的半径,所以y=-1总与该圆相切.
MN,即圆心到直线y=-1的距离等于圆的半径,所以y=-1总与该圆相切.
11. (2011山东东营,24,12分)(本题满分12分)
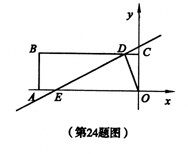
如图所示,四边形OABC是矩形,点A、C的坐标分别为(-3,0),(0,1),点
D是线段BC上的动点(与端点B、C不重合),过点D做直线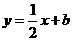 交折现OAB与点E。
交折现OAB与点E。
(1)记ΔODE的面积为S,求S与b的函数关系式;
(2)当点E在线段OA上时,且tan∠DEO=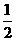 。若矩形OABC关于直线DE的对称图形为四边形
。若矩形OABC关于直线DE的对称图形为四边形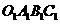 ,试探究四边形
,试探究四边形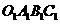 与矩形OABC的重叠部分的面积是否发生变化,如不变,求出该重叠部分的面积;若改变,请说明理由。
与矩形OABC的重叠部分的面积是否发生变化,如不变,求出该重叠部分的面积;若改变,请说明理由。
[答案]
解(1)由题意得B(-3,1).若直线经过点A(-3,0)时,则b=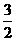 ;
;
若直线经过点B(-3,1)时,则b=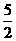 ;
;
若直线经过点C(0,1)时,则b=1;
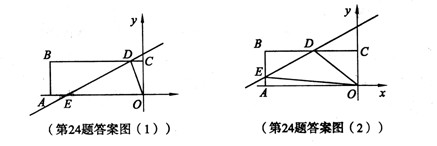
①若直线与折线OAB的交点在OA上时,即1<b≤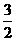 ,如图(1),此时E(-2b,0),∴S=
,如图(1),此时E(-2b,0),∴S=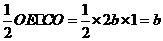
②若直线与折线OAB的交点在BA上时,即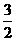 <b<
<b<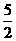 ,如图(2),此时点E(-3,b-
,如图(2),此时点E(-3,b-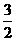 ),D(-2b+2,1)
),D(-2b+2,1)
∴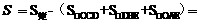
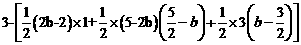
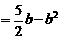
∴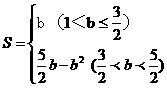
(2)如图3,设O1A1 与CB相交与点M,OA与C1B1相交与点N,则矩形O1A1 B1 C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。由题意知,DM∥NE,DN∥ME, ∴四边形DNEM为平行四边形,根据轴对称知,∠MED=∠NED,又∠MDE=∠NED,∴MD=ME,∴四边形DNEM为菱形。
过点D作DH⊥OA,垂足为H,依题意知,tan∠DEH=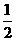 ,DH=1,
,DH=1,
∴ HE=2,设菱形DNEM的边长为a,则在Rt△DHN中,由勾股定理知: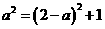 ,∴
,∴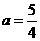 ∴
∴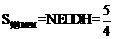
∴矩形O1A1 B1 C1与矩形OABC的重叠部分的面积不发生变化,面积始终为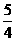
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com