
题目列表(包括答案和解析)
24、(2011•潍坊)如图,y关于x的二次函数y=﹣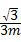 (x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
(x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
(1)写出A、B、D三点的坐标;
(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;
(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.

考点:二次函数综合题。
专题:压轴题;分类讨论。
分析:(1)根据x轴,y轴上点的坐标特征代入即可求出A、B、D三点的坐标;
(2)待定系数法先求出直线ED的解析式,再根据切线的判定得出直线与圆的位置关系;
(3)分当0<m<3时,当m>3时两种情况讨论求得关于m的函数.
解答:解:(1)A(﹣m,0),B(3m,0),D(0,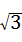 m).
m).
(2)设直线ED的解析式为y=kx+b,将E(﹣3,0),D(0,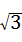 m)代入得:
m)代入得:
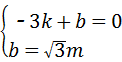 解得,k=
解得,k=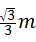 ,b=
,b=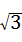 m.
m.
∴直线ED的解析式为y=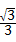 mx+
mx+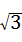 m.
m.
将y=﹣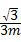 (x+m)(x﹣3m)化为顶点式:y=﹣
(x+m)(x﹣3m)化为顶点式:y=﹣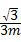 (x+m)2+
(x+m)2+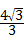 m.
m.
∴顶点M的坐标为(m,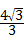 m).代入y=
m).代入y=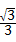 mx+
mx+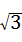 m得:m2=m
m得:m2=m
∵m>0,∴m=1.所以,当m=1时,M点在直线DE上.
连接CD,C为AB中点,C点坐标为C(m,0).
∵OD=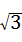 ,OC=1,∴CD=2,D点在圆上
,OC=1,∴CD=2,D点在圆上
又OE=3,DE2=OD2+OE2=12,
EC2=16,CD2=4,∴CD2+DE2=EC2.
∴∠FDC=90°
∴直线ED与⊙C相切.
(3)当0<m<3时,S△AED=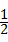 AE.•OD=
AE.•OD=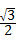 m(3﹣m)
m(3﹣m)
S=﹣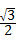 m2+
m2+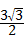 m.
m.
当m>3时,S△AED=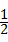 AE.•OD=
AE.•OD=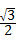 m(m﹣3).
m(m﹣3).
即S=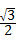 m2_
m2_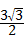 m.
m.
点评:本题是二次函数的综合题型,其中涉及的知识点有x轴,y轴上点的坐标特征,抛物线解析式的确定,抛物线的顶点公式和三角形的面积求法.注意分析题意分情况讨论结果.
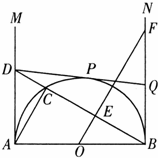
23、(2011•潍坊)如图,AB是半径O的直径,AB=2.射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.
(1)求证:△ABC∽△OFB;
(2)当△ABD与△BFO的面枳相等时,求BQ的长;
(3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点.
考点:切线的性质;全等三角形的判定与性质;勾股定理;圆周角定理;相似三角形的判定与性质。
专题:证明题;几何综合题。
分析:(1)根据OE∥AC,得出∠BAC=∠FOB,进而得出∠BCA=∠FBO=90°,从而证明结论;
(2)根据△ACB∽△OBF得出△ABD∽△BFO,从而得出DQ∥AB,即可得出BQ=AD;
(3)首先得出AD=DP,QB=BQ,进而得出DQ2=QK2+DK2,得出BF=2BQ,即可得出Q为BF的中点.
解答:证明:(1)∵AB为直径,
∴∠ACB=90°,即:AC⊥BC,
又OE⊥BC,
∴OE∥AC,
∴∠BAC=∠FOB,
∵BN是半圆的切线,
∴∠BCA=∠FBO=90°,
∴△ACB∽△OBF.
解:(2)由△ACB∽△OBF得,∠OFB=∠DBA,∠DAB=∠OBF=90°,
∴△ABD∽△BFO,
当△ABD与△BFO的面积相等时,△ABD≌△BFO,
∴AD=1,
又DPQ是半圆O的切线,
∴OP=1,且OP⊥DP,
∴DQ∥AB,
∴BQ=AD=1,
(3)由(2)知,△ABD∽△BFO,
∴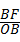 =
=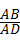 ,
,
∴BF=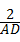 ,
,
∵DPQ是半圆O的切线,
∴AD=DP,QB=BQ,
过Q点作AM的垂线QK,垂足为K,在直角三角形DQK中,
DQ2=QK2+DK2,
∴(AD+BQ)2=(AD﹣BQ)2+22.
∴BQ=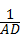 ,
,
∴BF=2BQ,
∴Q为BF的中点.
点评:此题主要考查了切线的性质以及全等三角形的判定和相似三角形的判定等知识,熟练利用相似三角形的判定是解决问题的关键.
22、(2011•潍坊)2010年上半年,某种农产品受不良炒作的影响,价格一路上扬.8月初国家实施调控措施后,该农产品的价格开始回落.其中,1月份至7月份,该农产品的月平均价格y元/千克与月份x呈一次函数关系;7月份至12月份,月平均价袼y元/千克与月份x呈二次函数关系.已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
(1)分别求出当1≤x≤7和7≤x≤12时,y关于x的函数关系式;
(2)2010年的12个月中.这种农产品的月平均价格哪个月最低?最低为多少?
(3)若以12个月份的月平均价格的平均数为年平均价格,月平均价格高于年平均价格的月份有哪些?
考点:二次函数的应用;一次函数的应用。
专题:销售问题。
分析:(1)根据自变量的不同取值范围内不同的函数关系设出不同的函数的解析式,利用待定系数法求得函数的解析式即可;
(2)根据一次函数的增减性和二次函数的最值确定该农产品的最低月份和最低价格即可;
(3)分别计算5个月的平均价格和年平均价格,比较得到结论即可.
解答:解:(1)当1≤x≤7时,设y=kx+m
将点(1,8)、(7,26)分别代入y=kx+m得:
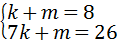 解之得:
解之得: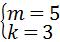
∴函数的解析式为:y=3x+5
当7≤x≤12时,设y=ax2+bx+c
将点(7,26)、(9,14)、(12,11)代入y=ax2+bx+c
得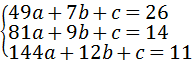 解之得:
解之得: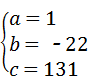
∴函数的解析式为y=x2﹣22x+131
(2)当1≤x≤7时,y=3x+5为增函数,
当x=1时,y有最小值8.
当7≤x≤12时,y=x2﹣22x+131=(x﹣11)2+10,
当x=11时,y有最小值为10.
所以,该农产品月平均价格最低的是1月,最低为8元/千克.
(3)∵1至7月份的月平均价格呈一次函数,
∴x=4时的月平均价格17是前7个月的平均值.
将x=8和x=10代入y=x2﹣22x+131
得y=19和y=11,
∴后5个月的月平均价格分别为19、14、11、10、11,
∴年平均价格为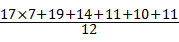 ≈15.3元/千克,
≈15.3元/千克,
当x=3时,y=14<15.3,
∴4,5,6,7,8这五个月的月平均价格高于年平均价格.
点评:本题考查了二次函数的应用,解决此类问题的关键是从实际问题中整理出函数模型,利用函数的知识解决实际问题.
21、(2011•潍坊)2010年秋冬北方严重干早,凤凰社区人畜饮用水紧张.毎天需从社区外调运饮用水120吨,有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂毎天最多可调出80吨,乙厂毎天最多可调出90吨.从两水厂运水到凤凰社区供水点的路程和运费如下表:
|
|
到凤凰社区供水点的路程(千米) |
运费(元/吨•千米) |
|
甲厂 |
20 |
12 |
|
乙厂 |
14 |
15 |
(1)若某天调运水的总运费为26700元,则从甲、乙两水厂各调运了多少吨饮用水?
(2)设从甲厂调运饮用水x吨,总运费为W元.试写出W关于与x的函数关系式,怎样安排调运方案才能使毎天的总运费最省?
考点:一次函数的应用;二元一次方程组的应用;一元一次不等式的应用。
专题:优选方案问题。
分析:(1)设设从甲厂调运了x吨饮用水,从甲厂调运了y吨饮用水,然后根据题意毎天需从社区外调运饮用水120吨与某天调运水的总运费为26700元列方程组即可求得答案;
(2)首先根据题意求得一次函数W=20×12x+14×15(120﹣x),又由甲厂毎天最多可调出80吨,乙厂毎天最多可调出90吨,确定x的取值范围,则由一次函数的增减性即可求得答案.
解答:解:(1)设从甲厂调运了x吨饮用水,从甲厂调运了y吨饮用水,
由题意得: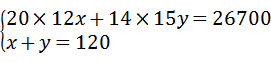 ,
,
解得: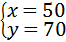 ,
,
∵50≤80,70≤90,
∴符合条件,
∴从甲、乙两水厂各调运了50吨、0吨吨饮用水;
(2)从甲厂调运饮用水x吨,则需从乙调运水120﹣x吨,
∵x≤80,且120﹣x≤90,
∴30≤x≤80,
总运费W=20×12x+14×15(120﹣x)=30x+25200,
∵W随X的增大而增大,
∴当x=30时,W最小=26100元,
∴每天从甲厂调运30吨,从乙厂调运90吨,每天的总运费最省.
点评:此题考查了二元一次方程组与一次函数的实际应用.此题难度适中,解题的关键是理解题意,抓住等量关系.
20、(2011•潍坊)甲、乙两个盒子中装有质地、大小相同的小球.甲盒中有2个白球、1个黄球和1个蓝球;乙盒中有1个白球、2个黄球和若干个蓝球.从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍.
(1)求乙盒中蓝球的个数;
(2)从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
考点:列表法与树状图法;分式方程的应用;概率公式。
专题:计算题。
分析:(1)由甲盒中有2个白球、1个黄球和1个蓝球,即可求得从甲盒中任意摸取一球,摸得篮球的概率,又由乙盒中有1个白球、2个黄球和若干个蓝球,可设乙盒中有x个篮球,则可求得从乙盒中任意摸取一球,摸得篮球的概率,根据从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍,列方程即可求得答案;
(2)采用列表法或树状图法,求得所有可能的结果与符合条件的情况数目;二者的比值就是其发生的概率.
解答:解:(1)设乙盒中有x个篮球,则从乙盒中任意摸取一球,摸得篮球的概率为:P1=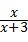 ,
,
从甲盒中任意摸取一球,摸得篮球的概率P2=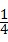 ;
;
依题意得: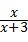 =
=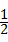 ,
,
解得:x=3,
∴乙盒中蓝球的个数是3个;
(2)列表得:
∴可能的结果有2种,其中均为篮球的有3种,
∴从甲、乙两盒中分别任意摸取一球,这两球均为蓝球的概率为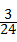 =
=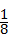 .
.

点评:本题考查的是用列表法或画树状图法求概率与古典概率的知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
19、(2011•潍坊)今年“五一“假期.某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°.已知A点海拔121米.C点海拔721米.
(1)求B点的海拔;
(2)求斜坡AB的坡度.

考点:解直角三角形的应用-坡度坡角问题;解直角三角形的应用-仰角俯角问题。
专题:应用题。
分析:(1)过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足,构造直角三角形ABE和直角三角形CBD,然后解直角三角形.
(2)求出BE的长,根据坡度的概念解答.
解答:解:如图,过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足.
在C点测得B点的俯角为30°,
∴∠CBD=30°,又BC=400米,
∴CD=400×sin30°=400×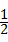 =200(米).
=200(米).
∴B点的海拔为721﹣200=521(米).

(2)∵BE=DF=CF﹣CD=521﹣121=400米,
∴AB=1040米,AE=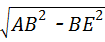 =
=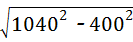 =960米,
=960米,
∴AB的坡度iAB=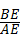 =
=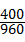 =
=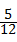 ,故斜坡AB的坡度为1:2.4.
,故斜坡AB的坡度为1:2.4.
点评:此题将坡度的定义与解直角三角形相结合,考查了同学们应用数学知识解决简单实际问题的能力,是一道中档题.
18、(2011•潍坊)已知正方形ABCD的边长为a,两条对角线AC、BD相交于点O,P是射线AB上任意一点,过P点分别作直线AC、BD的垂线PE、PF,垂足为E、F.

(1)如图1,当P点在线段AB上时,求PE+PF的值.
(2)如图2,当P点在线段AB的延长线上时,求PE﹣PF的值.
考点:正方形的性质;矩形的判定与性质;解直角三角形。
专题:几何图形问题。
分析:(1)因为ABCD是正方形,所以对角线互相垂直,又因为过P点分别作直线AC、BD的垂线PE、PF,垂足为E、F,所以可证明四边形PFOE是矩形,从而求出解.
(2)因为ABCD是正方形,所以对角线互相垂直,又因为过P点分别作直线AC、BD的垂线PE、PF,垂足为E、F,所以可证明四边形PFOE是矩形,从而求出解.
解答:解:(1)∵ABCD是正方形,
∴AC⊥BD,∵PF⊥BD,∴PF∥AC,同理PE∥BD,
∴四边形PFOE为矩形,故PE=OF.
又∵∠PBF=45°,∴PF=BF.
∴PE+PF=OF+FB=OB=acos45°=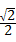 a.
a.
(2)∵ABCD是正方形,
∴AC⊥BD,∵PF⊥BD,∴PF∥AC,同理PE∥BD,
∴四边形PFOE为矩形,故PE=OF.
又∵∠PBF=∠OBA=45°,∴PF=BF.
∴PE﹣PF=OF﹣BF=OB=acos45°=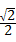 a.
a.
点评:本题考查正方形的性质,正方形的对角线互相垂直且平分每一组对角,四边相等,四个角都是直角,以及矩形的判定和性质解直角三角形等.
17、(2011•潍坊)已知长方形ABCD,AB=3cm,AD=4cm,过对角线BD的中点O做BD垂直平分线EF,分别交AD、BC于点E、F,则AE的长为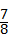 cm .
cm .
考点:勾股定理;线段垂直平分线的性质;矩形的性质。
专题:几何图形问题。
分析:连接EB,构造直角三角形,设AE为x,则DE=BE=4﹣x,利用勾股定理得到有关x的一元一次方程,求得即可.
解答:解:连接EB,
∵BD垂直平分EF,
∴ED=EB,
设AE=xcm,则DE=EB=(4﹣x)cm,
在Rt△AEB中,
AE2+AB2=BE2,
即:x2+32=(4﹣x)2,
解得:x=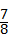
故答案为: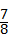 cm.
cm.
点评:本题考查了勾股定理的内容,利用勾股定理不单单能在直角三角形中求边长,而且能利用勾股定理这一隐含的等量关系列出方程.
16、(2011•潍坊)已知线段AB的长为a,以AB为边在AB的下方作正方形ACDB.取AB边上一点E,以AE为边在AB的上方作正方形AENM.过E作EF丄CD,垂足为F点.若正方形AENM与四边形EFDB的面积相等,則AE的长为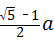 .
.

考点:一元二次方程的应用。
专题:几何图形问题。
分析:本题需先设出AE的长,从而得出BE的长,再根据题意列出方程,求出x的值即可得出AE的长.
解答:解:设AE的长为x,则BE的长为a﹣x
根据题意得:x2=(a﹣x)•a
解得:x=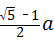
故答案为: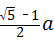 .
.
点评:本题主要考查了一元二次方程的应用,在解题时要根据已知条件和图形列出方程是本题的关键.
15、(2011•潍坊)方程组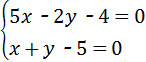 的解是
的解是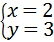 .
.
考点:解二元一次方程组。
专题:计算题。
分析:由于方程组中两方程y的系数是倍数关系,且数值较小,故可先用加减消元法再用代入消元法求解.
解答:解: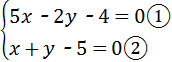 ,②×2+①得,7x﹣14=0,解得x=2;
,②×2+①得,7x﹣14=0,解得x=2;
把x=2代入②得,2+y﹣5=0,解得y=3.
故原方程组的解为: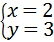 .
.
故答案为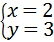 .
.
点评:本题考查的是解二元一次方程组的加减消元法和代入消元法,比较简单.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com