
题目列表(包括答案和解析)
34. (2011内蒙古乌兰察布,24,16分)如图,正比例函数和反比例函数的图象都经过点 A ( 3 , 3) ,把直线 OA 向下平移后,与反比例函数的图象交于点B(6,m),与x轴、y
轴分别交于C、D两点
(1)求 m的值;
( 2 )求过 A、B、D 三点的抛物线的解析式;
( 3 )若点E是抛物线上的一个动点,是否存在点 E ,使四边形 OECD 的面积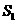 ,是四边形OACD 面积
,是四边形OACD 面积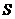 的
的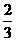 ?若存在,求点 E 的坐标;若不存在,请说明理由.
?若存在,求点 E 的坐标;若不存在,请说明理由.

[答案]⑴设反比例函数的解析式为: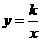 ,把
,把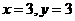 代人解析式中求得
代人解析式中求得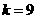 .当
.当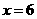 时,
时,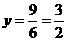 ,所以
,所以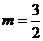 ;
;
⑵设直线OA的解析式为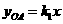 ,把
,把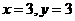 代人解析式中求得
代人解析式中求得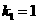 ,则有
,则有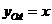 ,
,
设直线BD的解析式为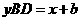 ,把
,把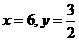 代人解析式中求得
代人解析式中求得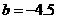 ,则有
,则有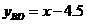 ,所以B(6,1.5)、D(0,-4.5)
,所以B(6,1.5)、D(0,-4.5)
设抛物线的解析式为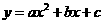 由题意知
由题意知
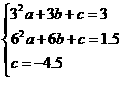 解得
解得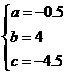
所以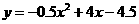
⑶由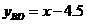 求出C(4.5,0),四边形OACD 面积
求出C(4.5,0),四边形OACD 面积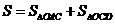 =
=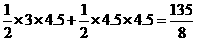 ,
,
四边形
OECD 的面积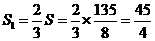
经分析点E在x轴的上方,四边形
OECD 的面积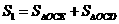
则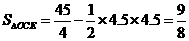 所以
所以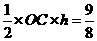 ,求出
,求出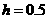 即点E的纵坐标是
即点E的纵坐标是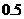 ,把
,把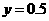 代人
代人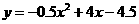 中得出
中得出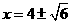 ,所以E(
,所以E(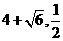 )或E(
)或E(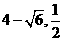 ).
).
33. (2011山东东营,23,10分)(本题满分10分)在平面直角坐标系中,现将一块等腰直角三角形ABC放在第一象限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),如图所示;抛物线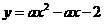 经过点B。
经过点B。
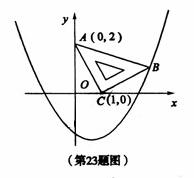
(1) 求点B的坐标;
(2) 求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使ΔACP仍然是以AC为直角边的等腰直角三角形?若存在,求所以点P的坐标;若不存在,请说明理由。
[答案]解:(1)过点B作BD⊥x轴,垂足为D,∵∠BCD+∠ACO=90° ,∠ACO+∠OAC =90°;
∴∠BCD=∠CAO; 又∵∠BDC=∠COA=90°;CB=AC,
∴ △BDC≌△CAO=90°,∴BD=OC=1,CD=OA=2;∴点B的坐标为(3,1)
(2)抛物线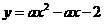 经过点B(3,1),则得
经过点B(3,1),则得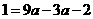 解得
解得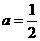 ,所以抛物线的解析式为
,所以抛物线的解析式为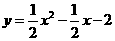
(3)假设存在点P,似的△ACP是直角三角形:
①若以AC为直角边,点C为直角顶点;则延长BC至点P1 使得P1C=BC,得到等腰直角三角形ACP1,过点P1作P1M⊥x轴,如图(1)。
∵CP1=BC,∠MCP1=∠BCD, ∠P1MC=∠BDC=90°,∴△MCP1≌△BCD
∴ CM=CD=2,P1M=BD=1,可求得点P1(-1,-1);经检验点P1(-1,-1)在抛物线为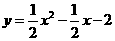 上;
上;
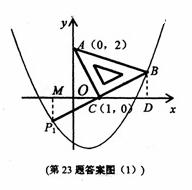
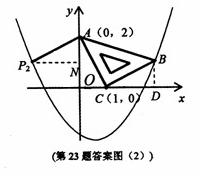
②若以AC为直角边, 点A为直角顶点;则过点A作AP2⊥CA,且使得AP2=AC,得到等腰直角三角形ACP2,过点P2作P2N⊥y轴,如图(2)。同理可得△AP2N≌△CAO;∴NP2=OA=2,AN=OC=1,可求得点P2(-2,1),;经检验点P2(-2,1)也在抛物线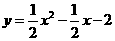 上;
上;
③若以AC为直角边, 点A为直角顶点;则过点A作AP3⊥CA,且使得AP3=AC,得到等腰直角三角形ACP3,过点P3作P3H⊥y轴,如图(3)同理可得△AP3H≌△CAO;∴HP3=OA=2,AH=OC=1,可求得点P3(2,3),;经检验点P3(2,3)不抛物线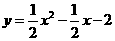 上;
上;
故符合条件的点有P1(-1,-1),P2(-2,1)两个。
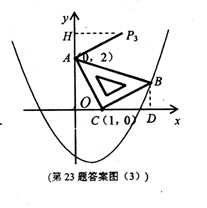
32.(2011湖南永州,24,10分)如图,已知二次函数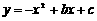 的图象经过A(
的图象经过A(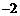 ,
,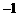 ),B(0,7)两点.
),B(0,7)两点.
⑴求该抛物线的解析式及对称轴;
⑵当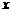 为何值时,
为何值时,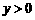 ?
?
⑶在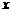 轴上方作平行于
轴上方作平行于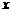 轴的直线
轴的直线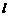 ,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作
,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作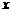 轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.

[答案]解:⑴把A(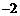 ,
,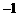 ),B(0,7)两点的坐标代入
),B(0,7)两点的坐标代入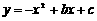 ,得
,得
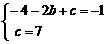 解得
解得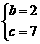
所以,该抛物线的解析式为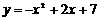 ,
,
又因为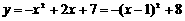 ,所以对称轴为直线
,所以对称轴为直线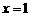 .
.
⑵当函数值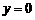 时,
时,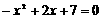 的解为
的解为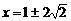 ,
,
结合图象,容易知道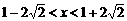 时,
时,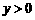 .
.
⑶当矩形CDEF为正方形时,设C点的坐标为(m,n),
则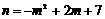 ,即
,即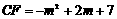
因为C,D两点的纵坐标相等,所以C,D两点关于对称轴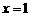 对称,设点D的横坐标为
对称,设点D的横坐标为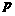 ,则
,则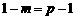 ,所以
,所以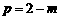 ,所以CD=
,所以CD=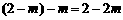
因为CD=CF,所以 ,整理,得
,整理,得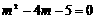 ,解得
,解得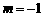 或5.
或5.
因为点C在对称轴的左侧,所以 只能取
只能取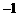 .
.
当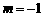 时,
时,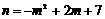 =
=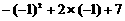 =4
=4
于是,得点C的坐标为(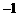 ,4).
,4).
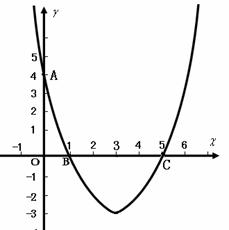
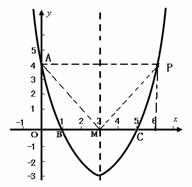
31. (2011广东茂名,25,8分)如图,在平面直角坐标系 中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴
中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴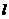 与
与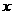 轴相交于点M.
轴相交于点M.
(1)求抛物线的解析式和对称轴; (3分)
(2)设点P为抛物线(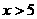 )上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标; (2分)
)上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标; (2分)
(3)连接AC.探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请你说明理由. (3分)
[答案]解:(1)根据已知条件可设抛物线的解析式为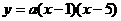 ,
,
把点A(0,4)代入上式得: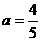 ,
,
∴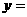
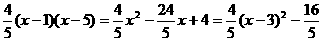 ,
,
∴抛物线的对称轴是: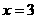 .
.
(2)由已知,可求得P(6,4).
提示:由题意可知以A、O、M、P为顶点的四边形有两条边AO=4、OM=3,又知点P的坐标中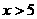 ,所以,MP>2,AP>2;因此以1、2、3、4为边或以2、3、4、5为边都不符合题意,所以四条边的长只能是3、4、5、6的一种情况,在Rt△AOM中,
,所以,MP>2,AP>2;因此以1、2、3、4为边或以2、3、4、5为边都不符合题意,所以四条边的长只能是3、4、5、6的一种情况,在Rt△AOM中,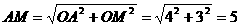 ,因为抛物线对称轴过点M,所以在抛物线
,因为抛物线对称轴过点M,所以在抛物线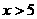 的图象上有关于点A的对称点与M的距离为5,即PM=5,此时点P横坐标为6,即AP=6;故以A、O、M、P为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立,
的图象上有关于点A的对称点与M的距离为5,即PM=5,此时点P横坐标为6,即AP=6;故以A、O、M、P为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立,
即P(6,4).
⑶法一:在直线AC的下方的抛物线上存在点N,使△NAC面积最大.
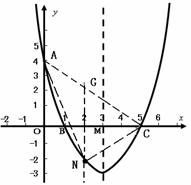
设N点的横坐标为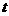 ,此时点N
,此时点N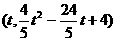 (
(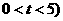 ,过点N作NG∥
,过点N作NG∥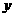 轴交AC于G;由点A(0,4)和点C(5,0)可求出直线AC的解析式为:
轴交AC于G;由点A(0,4)和点C(5,0)可求出直线AC的解析式为: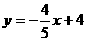 ;把
;把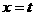 代入得:
代入得: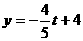 ,则G
,则G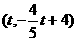 ,
,
此时:NG=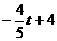 -(
-(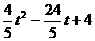 ),
),
=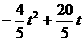 .
.
∴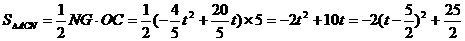
∴当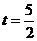 时,△CAN面积的最大值为
时,△CAN面积的最大值为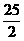 ,
,
由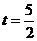 ,得:
,得: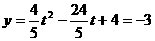 ,∴N(
,∴N(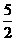 , -3).
, -3).
法二:提示:过点N作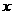 轴的平行线交
轴的平行线交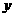 轴于点E,作CF⊥EN于点F,则
轴于点E,作CF⊥EN于点F,则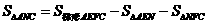
(再设出点N的坐标,同样可求,余下过程略)
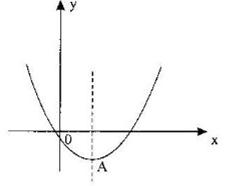
30. (2011湖北黄石,25,10分)已知二次函数y=x2-2mx+4m-8
(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围。
(2)以抛物线y=x2-2mx+4m-8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M、N两点在抛物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
(3)若抛物线y=x2-2mx+4m-8与x轴交点的横坐标均为整数,求整数m的值。
[答案]解:(1)∵x=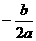 =m
=m
∴m≥2
(2) 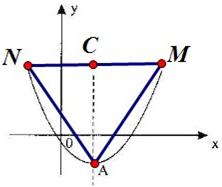
A(m,-m2+4m-8)
由对称性可知∠MAC=300
故设yAM=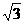 x+b
x+b
把A(m,-m2+4m-8)代入yAM=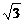 x+b
x+b
得,b=-m2+(4-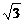 )m-8
)m-8
即yAM=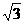 x-m2+(4-
x-m2+(4-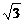 )m-8
)m-8
∴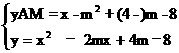
解之得x1=m,x2=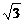 +m
+m
∴CM=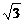
∴S△AMN=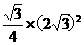 =3
=3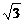
(3)x=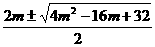 =m
=m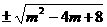
∵图象与x轴交点的横坐标均为整数
∴整数m=2
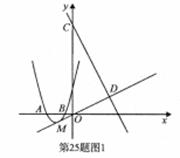
29. (2011湖北武汉市,25,12分)(本题满分12分)如图1,抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点.
(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=-2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围;
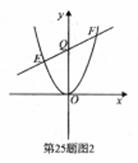
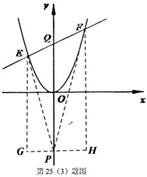
(3)如图2,将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于E,F两点.问在y轴的负半轴上是否存在点P,使△PEF的内心在y轴上.若存在,求出点P的坐标;若不存在,请说明理由.
[答案](1)抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点
∴9a-3b+3=0 且a-b+3=0
解得a=1 , b =4
∴抛物线的解析式为y=x2+4x+3
(2)由(1)配方得y=(x+2)2-1
∴抛物线的顶点M(-2,1)
∴直线OD的解析式为y=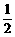 x
x
于是设平移的抛物线的顶点坐标为(h,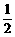 h),
h),
∴平移的抛物线解析式为y=(x-h)2+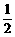 h.
h.
①当抛物线经过点C时,∵C(0,9),∴h2+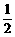 h=9,
h=9,
解得h=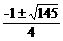 .
.
∴ 当 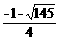 ≤h<
≤h<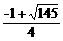 时,平移的抛物线与射线CD只有一个公共点.
时,平移的抛物线与射线CD只有一个公共点.
②当抛物线与直线CD只有一个公共点时,
由方程组y=(x-h)2+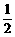 h,y=-2x+9.
h,y=-2x+9.
得 x2+(-2h+2)x+h2+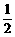 h-9=0,
h-9=0,
∴△=(-2h+2)2-4(h2+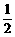 h-9)=0,
h-9)=0,
解得h=4.
此时抛物线y=(x-4)2+2与射线CD唯一的公共点为(3,3),符合题意.
综上:平移的抛物线与射线CD只有一个公共点时,顶点横坐标的值或取值范围是 h=4或 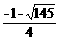 ≤h<
≤h<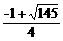 .
.
(3)方法1
将抛物线平移,当顶点至原点时,其解析式为y=x2,
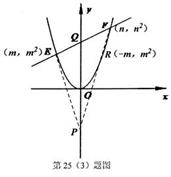
 设EF的解析式为y=kx+3(k≠0).
设EF的解析式为y=kx+3(k≠0).
假设存在满足题设条件的点P(0,t),如图,过P作GH∥x轴,分别过E,F作GH的垂线,垂足为G,H.
∵△PEF的内心在y轴上,
∴∠GEP=∠EPQ=∠QPF=∠HFP,∴△GEP∽△HFP,
∴GP/PH=GE/HF,
∴-xE/xF=(yE-t)/(yF-t)=(kxE+3-t)/(kxF+3-t)
∴2kxE·xF=(t-3)(xE+xF)
由y=x2,y=-kx+3.得x2-kx-3=0.
∴xE+xF=k,xE·xF=-3.
∴2k(-3)=(t-3)k
∵k≠0,∴t=-3.
∴y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上.
方法2 :设EF的解析式为y=kx+3(k≠0),点E,F的坐标分别为(m,m2)(n,n2)由方法1知:mn=-3.作点E关于y轴的对称点R(-m,m2),作直线FR交y轴于点P,由对称性知∠EPQ=∠FPQ,∴点P就是所求的点.
由F,R的坐标,可得直线FR的解析式为y=(n-m)x+mn.
当x=0,y=mn=-3,
∴P(0,-3).
∴y轴的负半轴上存在点P(0,-3),使△PEF的内心在y轴上.
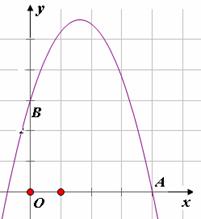
28. (2011江苏淮安,26,10分)如图,已知二次函数y= -x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.
(1)求此二次函数关系式和点B的坐标;
(2)在x轴的正半轴上是否存在点P,使得△PAB是以AB为底的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
[答案]解:(1)∵二次函数y= -x2+bx+3的图象与x轴的一个交点为A(4,0),
∴0= -42+4b+3,
解得b=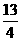 ,
,
∴此二次函数关系式为:y= -x2+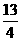 x+3,
x+3,
点B的坐标为B(0,3).
(2)在x轴的正半轴上是否存在点P(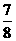 ,0),使得△PAB是以AB为底的等腰三角形.理由如下:
,0),使得△PAB是以AB为底的等腰三角形.理由如下:
设点P(x,0),x>0,则根据下图和已知条件可得
x2+ 32=(4- x)2,
解得x=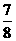 ,
,
∴点P的坐标为P(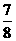 ,0).
,0).
即,在x轴的正半轴上是否存在点P(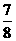 ,0),使得△PAB是以AB为底的等腰三角形.
,0),使得△PAB是以AB为底的等腰三角形.
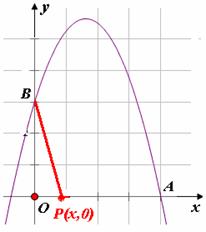
27. (2011江西南昌,24,10分)将抛物线c1:y=-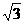 x2+
x2+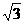 沿x轴翻折,得抛物线c2,如图所示.
沿x轴翻折,得抛物线c2,如图所示.
(1)请直接写出抛物线c2的表达式.
(2)现将抛物线c1向左平移m个单位长度,平移后得的新抛物线的顶点为M,与x轴的交点从左到右依次为A,B;将抛物线c2向右也平移m个单位长度,平移后得到的新抛物线的顶点为N,与x轴交点从左到右依次为D,E.
①当B,D是线段AE的三等分点时,求m的值;
②在平移过程中,是否存在以点A,N,E,M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
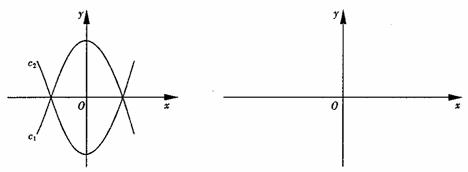
备用图
[答案]解:(1)y=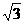 x2-
x2-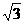 .
.
(2)①令-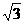 x2+
x2+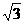 =0,得x1=-1,x2=1,则抛物线c1与x轴的两个交点坐标为(-1,0),(1,0).∴A(-1-m,0),B(1+m,0).
=0,得x1=-1,x2=1,则抛物线c1与x轴的两个交点坐标为(-1,0),(1,0).∴A(-1-m,0),B(1+m,0).
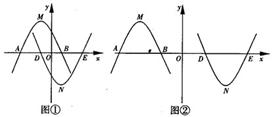
当AD=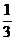 AE时,如图①,(-1+m)-(-1-m)=
AE时,如图①,(-1+m)-(-1-m)=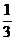 [(1+m)-(-1-m)], ∴m=
[(1+m)-(-1-m)], ∴m=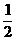
当AB=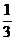 AE时,如图②,(1-m)-(-1-m)=
AE时,如图②,(1-m)-(-1-m)=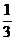 [(1+m)-(-1-m)], ∴m=2.
[(1+m)-(-1-m)], ∴m=2.
∴当m=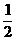 或2时,B,D是线段AE的三等分点.
或2时,B,D是线段AE的三等分点.
②存在.理由:连接AN、NE、EM、MA.依题意可得:M(-m,-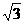 ).即M,N关于原点O对称,∴OM=ON.∵A(-1-m,0),E(1+m,0),∴A,E关于原点O对称,∴OA=OE,∴四边形ANEM为平行四边形.要使平行四边形ANEM为矩形,必需满足OM=OA,即m2+(
).即M,N关于原点O对称,∴OM=ON.∵A(-1-m,0),E(1+m,0),∴A,E关于原点O对称,∴OA=OE,∴四边形ANEM为平行四边形.要使平行四边形ANEM为矩形,必需满足OM=OA,即m2+(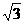 )2=[-(-1-m)]2, ∴m=1.
)2=[-(-1-m)]2, ∴m=1.
∴当m=1时,以点A,N,E,M为顶点的四边形是矩形.
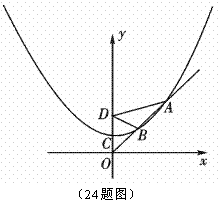
26. (2011四川宜宾,24,12分)已知抛物线的顶点是C(0,a)(a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.
⑴求含有常数a的抛物线的解析式;
⑵设点P是抛物线上任意一点,过P作PH⊥x轴,垂足是H,求证:PD=PH;
⑶设过原点O的直线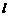 与抛物线在第一象限相交于A、B两点,若DA=2DB,且
与抛物线在第一象限相交于A、B两点,若DA=2DB,且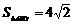 ,求a的值.
,求a的值.

[答案]解:⑴设抛物线的解析式为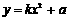
∵点D(2a,2a)在抛物线上,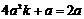
∴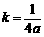
∴抛物线的解析式为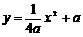
⑵设抛物线上一点P(x,y),过P作PH⊥x轴,PG⊥y轴,在 中,由勾股定理得:
中,由勾股定理得:
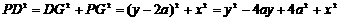
∵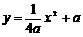 ∴
∴
∴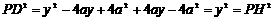
∴PD=PH.
⑶过B点BE⊥x轴,AF⊥y轴,
由⑵的结论:BE=DB AF=DA
∵DA=2DB ∴AF=2BE ∴AO=2BO
∴B是OA的中点
∵C是OD的中点
连接BC
∴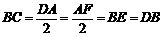
过B作BR⊥y轴,
∵BR⊥CD ∴CR=DR, 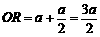 ,
,
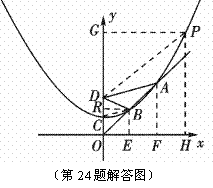 ∴B点的纵坐标是
∴B点的纵坐标是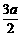 ,又点B在抛物线上
,又点B在抛物线上
∴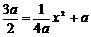 ∴
∴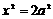
∵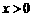 ∴
∴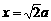 ∴B(
∴B(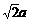 ,
,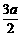 )
)
AO=2OB, ∴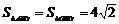
所以,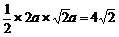
∴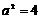 , ∵
, ∵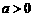 ∴
∴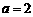
25. (2011四川广安,30,12分)如图9所示,在平面直角坐标系中,四边形ABCD是直角梯形,BC∥AD,∠BAD= 90°,BC与y轴相交于点M,且M是BC的中点,A、B、D三点的坐标分别是A(-1.0),B( -1.2),D( 3.0),连接DM,并把线段DM沿DA方向平移到O/V,若抛物线y=ax2+bx+c经过点D、M、N。
(1)求抛物线的解析式
(2)抛物线上是否存在点P.使得PA= PC.若存在,求出点P的坐标;若不存在.请说明理由。
(3)设抛物线与x轴的另-个交点为E.点Q是抛物线的对称轴上的-个动点,当点Q在什么位置时有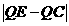 最大?并求出最大值。
最大?并求出最大值。
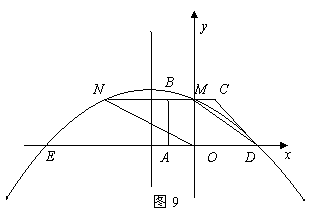

[答案](1)解:由题意可得M(0.2),N(-3.2)
∴ 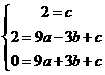
解得: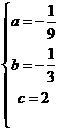
∴y=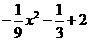
(2)∵PA= PC ∴P为AC的垂直平分线上,依题意,AC的垂直平分线经过(-1.2)(1.0) 所在的直线为y=-x+1
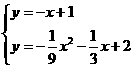
解得: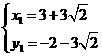
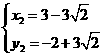
∴P1(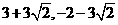 )P2(
)P2(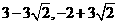 )
)
(3)D为E关于对称轴x=1.5对称
CD所在的直线y=-x+3
∴yQ=4.5 ∴Q(-1.5.4.5)
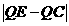 最大值为QC=
最大值为QC=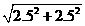 =
=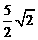
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com