
题目列表(包括答案和解析)
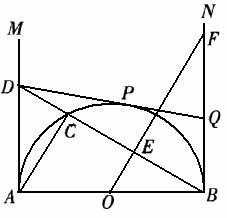
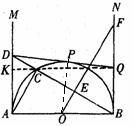
12. (2011山东潍坊,23,11分)如图,AB是半圆O的直径,AB=2.射线AM、BN为半圆的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点做半圆的切线DP,切点为P,与BN相交于点Q.
(1)求证:△ABC∽ΔOFB;
(2)当ΔABD与△BFO的面积相等时,求BQ的长;
(3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点.
[解](1)证明:∵AB为直径,
∴∠ACB=90°,即AC⊥BC.
又∵OE⊥BC,∴OE//AC,∴∠BAC=∠FOB.
∵BN是半圆的切线,故∠BCA=∠OBF=90°.
∴△ACB∽△OBF.
(2)由△ACB∽△OBF,得∠OFB=∠DBA,∠DAB=∠OBF=90°,
∴△ABD∽△BFO,
当△ABD与△BFO的面积相等时,△ABD≌△BFO.
∴AD=BO=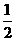 AB =1.
AB =1.
∵DA⊥AB,∴DA为⊙O的切线.
连接OP,∵DP是半圆O的切线,
∴DA=DP=1,∴DA=AO=OP=DP=1,
∴四边形ADPO为正方形.
∴DP//AB,∴四边形DABQ为矩形.
∴BQ=AD=1.
(3)由(2)知,△ABD∽△BFO,
∴ ,∴
,∴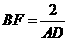 .
.
∵DPQ是半圆O的切线,∴AD=DP,QB=QP.
过点Q作AM的垂线QK,垂足为K,在Rt△DQK中, ,
,
∴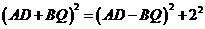 ,
,
∴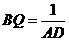 ,∴BF=2BQ,∴Q为BF的中点.
,∴BF=2BQ,∴Q为BF的中点.
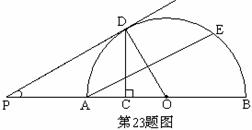
11. (2011山东聊城,23,8分)如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是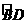 的中点,连接OD、AE,过点D作DP∥AE交BA的延长线于点P,
的中点,连接OD、AE,过点D作DP∥AE交BA的延长线于点P,
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线;
[答案](1)∵点C是OA的中点,∴OC=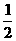 OA=
OA=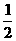 OD,∵CD⊥OA,∴∠OCD=90°,在Rt△OCD中,cos∠COD=
OD,∵CD⊥OA,∴∠OCD=90°,在Rt△OCD中,cos∠COD= ,∴∠COD=60°,即∠AOD=60°,
,∴∠COD=60°,即∠AOD=60°,
(2)证明:连接OC,点E是BD弧的中点,DE弧=BE弧,∴∠BOE=∠DOE=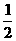 ∠DOB=
∠DOB=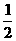 (180°-∠COD)=60°,∵OA=OE,∴∠EAO=∠AEO,又∠EAO+∠AEO=∠EOB=60°,∴∠EAO=30°,∵PD∥AE,∴∠P=∠EAO=30°,由(1)知∠AOD=60°,∴∠PDO=180°-(∠P+∠POD)=180°-(30°+60°)=90°,∴PD是圆O的切线
(180°-∠COD)=60°,∵OA=OE,∴∠EAO=∠AEO,又∠EAO+∠AEO=∠EOB=60°,∴∠EAO=30°,∵PD∥AE,∴∠P=∠EAO=30°,由(1)知∠AOD=60°,∴∠PDO=180°-(∠P+∠POD)=180°-(30°+60°)=90°,∴PD是圆O的切线
10.(2011山东济宁,20,7分)如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF,
(1)求证:OD∥BE;
(2)猜想:OF与CD有何数量关系?并说明理由.


[答案](1)证明:连接OE,
∵AM、DE是⊙O的切线,OA、OE是⊙O的半径,
∴∠ADO=∠EDO,∠DAO=∠DEO=90°,
∴∠AOD=∠EOD=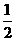 ∠AOE,
∠AOE,
∵∠ABE=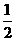 ∠AOE,∴∠AOD=∠ABE,
∠AOE,∴∠AOD=∠ABE,
∴OD∥BE
(2)OF=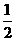 CD,
CD,
理由:连接OC,
∵BC、CE是⊙O的切线,
∴∠OCB=∠OCE
∵AM∥BN,
∴∠ADO+∠EDO+∠OCB+∠OCE=180°
由(1)得∠ADO=∠EDO,
∴2∠EDO+2∠OCE=180°,即∠EDO+∠OCE=90°
在Rt△DOC中,∵F是DC的中点,
∴OF=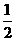 CD.
CD.
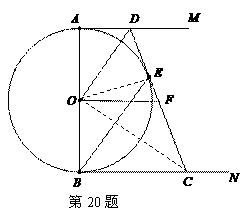

9. (2011广东株洲,22,8分)如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D 为AC上一点,∠AOD=∠C.
(1)求证:OD⊥AC;
(2)若AE=8,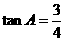 ,求OD的长.
,求OD的长.
[答案](1)证明:∵BC是⊙O的切线,AB为⊙O的直径
∴∠ABC=90°,∠A+∠C=90°,
又∵∠AOD=∠C,
∴∠AOD+∠A=90°,
∴∠ADO=90°,
∴OD⊥AC.
(2)解:∵OD⊥AE,O为圆心,
∴D为AE中点 ,
∴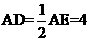 ,
,
又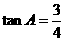 ,∴ OD=3.
,∴ OD=3.
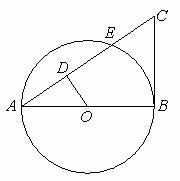
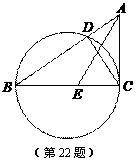
8. (2011浙江省嘉兴,22,12分)如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC=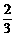 ,tan∠AEC=
,tan∠AEC=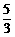 ,求圆的直径.
,求圆的直径.

[答案](1)∵BC是直径,∴∠BDC=90°,∴∠ABC+∠DCB=90°,∵∠ACD=∠ABC,
∴∠ACD+∠DCB=90°,∴BC⊥CA,∴CA是圆的切线.
(2)在Rt△AEC中,tan∠AEC=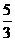 ,∴
,∴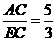 ,
,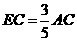 ;
;
在Rt△ABC中,tan∠ABC=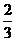 ,∴
,∴ ,
,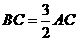 ;
;
∵BC-EC=BE,BE=6,∴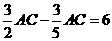 ,解得AC=
,解得AC= ,
,
∴BC=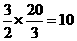 .即圆的直径为10.
.即圆的直径为10.
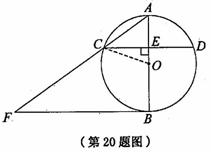
7. (2011浙江温州,20,8分)如图,AB是⊙O的直径,弦CD⊥AB于点E,过点B作⊙O的切线,交AC的延长线于点F.已知OA=3,AE=2,
(1)求CD的长;
(2)求BF的长.
[答案]解:(1)连结OC,在Rt△OCE中,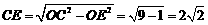 .
.
∵CD⊥AB,
∴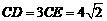
(2) ∵BF是⊙O 的切线,
∴FB⊥AB,
∴CE∥FB,
∴△ACE∽△AFB,
∴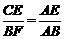 ,
,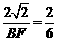 ,
,
∴
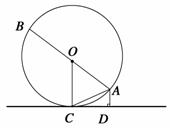
6. (2011山东日照,21,9分)如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.
求证:(1)∠AOC=2∠ACD;
(2)AC2=AB·AD.
[答案]证明:(1)∵CD是⊙O的切线,∴∠OCD=90°,
即∠ACD+∠ACO=90°.…① ∵OC=OA,∴∠ACO=∠CAO,
∴∠AOC=180°-2∠ACO,即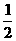 ∠AOC+∠ACO=90°. ② 由①,②,得:∠ACD-
∠AOC+∠ACO=90°. ② 由①,②,得:∠ACD-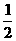 ∠AOC=0,即∠AOC=2∠ACD;
∠AOC=0,即∠AOC=2∠ACD;
(2)如图,连接BC.
∵AB是直径,∴∠ACB=90°.
在Rt△ACD与△RtACD中,
∵∠AOC=2∠B,∴∠B=∠ACD,
∴△ACD∽△ABC,∴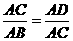 ,即AC2=AB·AD.
,即AC2=AB·AD.
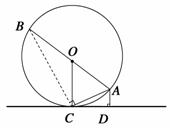
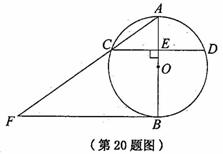
5. (2011山东菏泽,18,10分)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.


解:(1)证明:∵AB=AC,∴∠ABC=∠C,
∵∠C=∠D,∴∠ABC=∠D,
又∵∠BAE=∠EAB,∴△ABE∽△ADB,
(2)
∵△ABE∽△ADB,∴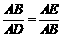 ,
,
∴AB2=AD·AE=(AE+ED)·AE=(2+4)×2=12
∴AB=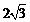 .
.
(3) 直线FA与⊙O相切,理由如下:
连接OA,∵BD为⊙O的直径,∴∠BAD=90°,
∴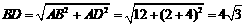 ,
,
BF=BO=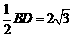 ,
,
∵AB=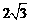 ,∴BF=BO=AB,可证∠OAF=90°,
,∴BF=BO=AB,可证∠OAF=90°,
∴直线FA与⊙O相切.
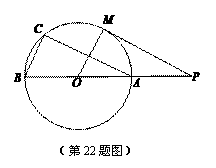
4. (2011山东滨州,22,8分)如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM, 连接OM、BC.
求证:(1)△ABC∽△POM;
(2)2OA2=OP·BC.

[答案]证明:(1)∵直线PM切⊙O于点M,∴∠PMO=90°………………1分
∵弦AB是直径,∴∠ACB=90°………………2分
∴∠ACB=∠PMO………………3分
∵AC∥PM, ∴∠CAB=∠P ………………4分
∴△ABC∽△POM………………5分
(2) ∵ △ABC∽△POM, ∴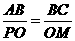 ………………6分
………………6分
又AB=2OA,OA=OM, ∴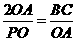 ………………7分
………………7分
∴2OA2=OP·BC………………8分
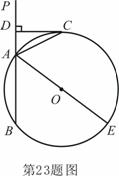
3. (2011安徽芜湖,23,12分)如图,已知直线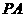 交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作
交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作 ,垂足为D.
,垂足为D.
(1) 求证:CD为⊙O的切线;
(2) 若DC+DA=6,⊙O的直径为10,求AB的长度.
[答案]
(1)证明:连接OC, ……………………………………1分
因为点C在⊙O上,OA=OC,所以 因为
因为 ,所以
,所以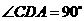 ,有
,有 .因为AC平分∠PAE,所以
.因为AC平分∠PAE,所以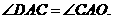 ……………3分
……………3分
所以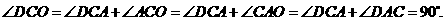 ……4分
……4分
又因为点C在⊙O上,OC为⊙O的半径,所以CD为⊙O的切线. ………………5分
(2)解:过O作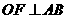 ,垂足为F,所以
,垂足为F,所以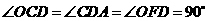 ,
,
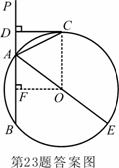 所以四边形OCDF为矩形,所以
所以四边形OCDF为矩形,所以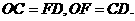 ……………………………7分
……………………………7分
因为DC+DA=6,设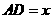 ,则
,则
因为⊙O的直径为10,所以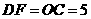 ,所以
,所以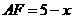 .
.
在 中,由勾股定理知
中,由勾股定理知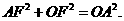
即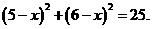 化简得
化简得 ,
,
解得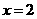 或x=9.
………………9分
或x=9.
………………9分
由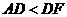 ,知
,知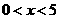 ,故
,故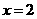 . ………10分
. ………10分
从而AD=2,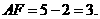 …………………11分
…………………11分
因为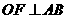 ,由垂径定理知F为AB的中点,所以
,由垂径定理知F为AB的中点,所以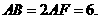 …………12分
…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com